Re
Esta entrada presenta algunas de las herramientas disponibles en R que permiten realizar análisis de conglomerados (o clusters) y representar los grupos y los resultados obtenidos en dendrogramas.
Introducción
El análisis de conglomerados jerárquico que abordamos en este post, en inglés Hierarchical Cluster Analysis, es una alternativa al conocido Análisis Cluster de k-Medias, que trataremos en una futura entrada. El Análisis de Conglomerados Jerárquico pretende identificar grupos homogéneos de variables en función de alguna característica. Consecuentemente, al realizar este proceso, se busca ir combinando las agrupaciones hasta que finalmente quede solamente un grupo con características más diferenciadas. Esta metodología para realizar conglomerados no requiere que se preestablezca un número de clusters determinado, como si necesita el Análisis de k-Medias, y suele completarse con la realización de un tipo de gráfico particular, llamado dendrograma, que permite visualizar las agrupaciones en forma de árbol donde se van representando los datos por subcategorías.
Paquetes
En primer lugar descargamos los paquetes requeridos para nuestro análisis:
library(dendextend)
library(factoextra)
library(NbClust)
library(pvclust)
library(flexclust)
library(readxl)
Dataset: Coeficientes de participación sectorial del VAB de las regiones peruanas
En esta ocasión vamos a trabajar con los coeficientes de participación sectorial del Valor Agregado Bruto por regiones de Perú para los años 2001 y 2012. Es decir, en los siguientes apartados se realizará un análisis de conglomerados jerárquico poniendo como pretexto examinar las similitudes entre regiones peruanas en función de su participación sectorial relativa en los años mencionados. Se buscará, por tanto, examinar similitudes regionales en términos de composición sectorial del VAB. En cierta medida este análisis podría servir como complemento del análisis realizado en este post anterior, donde se examinaba el peso sectorial de cada región peruana sobre la economía departamental y nacional en 2016.
La información sobre la participación relativa sectorial de las regiones peruanas las hemos obtenido del Instituto Nacional de Estadística e Informática del Perú (INEI). Como en este caso tenemos las participaciones sectoriales-regionales guardadas en un archivo excel en nuestro ordenador, empezamos cargando dichos archivos, uno para el año 2001 y otro para el año 2012, utilizando el paquete {readxl} y la función read_excel().
ddendvab01 <- read_excel("datasets/ddendvab01.xlsx")
ddendvab12 <- read_excel("datasets/ddendvab12.xlsx")
Como podemos ver, hemos clasificado la actividad productiva de las regiones en nueve grandes categorías o sectores productivos, donde en este caso la pesca se encuentra dentro de la categoría agrvab (agrícultura, caza y silvicultura). El resto de sectores son: minvab: minería y actividades extractivas; manvab: manufactura; convab: construcción; comvab: comercio; tycvab: transporte y comunicaciones; ryhvab: restaurantes y hoteles; sguvab: servicios gubernamentales y otrvab: otros servicios. Es conocido, tal y cómo quedó reflejado en este post arriba mencionado, la gran concentración productiva existente en algunas regiones del país. La actividad extractiva, por ejemplo, representa una gran proporción del VAB total en regiones como Cusco, Arequipa, Ancash entre otras, la agricultura resulta especialmente relevante en la región de Amazonas o las actividades de servicios lideran notablemente la economía de la región capitalina, Lima.
ddendvab01
## # A tibble: 24 x 10
## Name agrvab01 minvab01 manvab01 convab01 comvab01 tycvab01 ryhvab01 sguvab01
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 AMA 40.7 0.290 11.0 1.91 10.0 8.48 2.88 10.8
## 2 ANC 10.9 27.6 15.7 4.39 6.78 7.26 2.11 5.62
## 3 APU 27.4 0.905 10.2 9.10 13.8 3.36 4.24 18.2
## 4 ARE 15.3 5.96 18.8 5.80 16.9 8.67 2.97 4.14
## 5 AYA 27.4 2.51 12.2 5.05 16.2 4.46 2.38 16.1
## 6 CAJ 19.9 31.3 10.8 4.80 9.25 3.51 2.34 6.61
## 7 CUS 13.4 10.3 13.0 7.65 15.7 7.17 6.79 8.39
## 8 HUAV 17.0 7.98 3.04 1.04 5.97 1.46 1.10 7.72
## 9 HUAC 29.2 7.04 10.0 1.62 15.0 10.8 3.96 10.4
## 10 ICA 19.4 4.77 19.5 3.74 14.7 9.23 4.32 5.93
## # ... with 14 more rows, and 1 more variable: otrvab01 <dbl>
ddendvab12
## # A tibble: 24 x 10
## Name agrvab12 minvab12 manvab12 convab12 comvab12 tycvab12 ryhvab12 sguvab12
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 AMA 33.2 0.316 8.41 13.3 8.72 8.43 2.72 12.8
## 2 ANC 7.30 26.2 12.2 7.49 7.60 8.74 2.55 6.85
## 3 APU 24.0 0.542 8.12 17.1 11.9 3.12 4.20 20.7
## 4 ARE 12.4 8.64 17.3 13.9 14.5 8.51 2.87 3.99
## 5 AYA 18.8 10.2 7.69 17.5 12.9 4.07 2.20 14.7
## 6 CAJ 18.9 20.0 11.3 8.47 10.5 4.54 3.01 9.61
## 7 CUS 10.3 20.1 7.98 17.1 11.5 5.88 6.23 6.96
## 8 HUAV 14.0 8.07 3.02 2.14 7.36 2.00 1.47 12.6
## 9 HUAC 23.7 3.10 9.70 4.08 15.9 13.0 4.79 13.4
## 10 ICA 16.4 8.02 20.2 13.5 10.8 8.05 3.56 4.84
## # ... with 14 more rows, and 1 more variable: otrvab12 <dbl>
Antes de empezar a operar indicamos que los nombres de las filas (rownames) son los que se encuentran en la columna con el nombre name y, posteriormente, quitamos dicha columna de nuestro dataset dejando únicamente los valores sobre los que vamos a trabajar.
rownames(ddendvab01)<- ddendvab01$Name
rownames(ddendvab01)
## [1] "AMA" "ANC" "APU" "ARE" "AYA" "CAJ" "CUS" "HUAV" "HUAC" "ICA"
## [11] "JUN" "LLIB" "LAM" "LIM" "LORE" "MDD" "MOQ" "PAS" "PIU" "PUN"
## [21] "SMA" "TAC" "TUM" "UCA"
ddendvab01$Name <- NULL
ddendvab01
## # A tibble: 24 x 9
## agrvab01 minvab01 manvab01 convab01 comvab01 tycvab01 ryhvab01 sguvab01
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 40.7 0.290 11.0 1.91 10.0 8.48 2.88 10.8
## 2 10.9 27.6 15.7 4.39 6.78 7.26 2.11 5.62
## 3 27.4 0.905 10.2 9.10 13.8 3.36 4.24 18.2
## 4 15.3 5.96 18.8 5.80 16.9 8.67 2.97 4.14
## 5 27.4 2.51 12.2 5.05 16.2 4.46 2.38 16.1
## 6 19.9 31.3 10.8 4.80 9.25 3.51 2.34 6.61
## 7 13.4 10.3 13.0 7.65 15.7 7.17 6.79 8.39
## 8 17.0 7.98 3.04 1.04 5.97 1.46 1.10 7.72
## 9 29.2 7.04 10.0 1.62 15.0 10.8 3.96 10.4
## 10 19.4 4.77 19.5 3.74 14.7 9.23 4.32 5.93
## # ... with 14 more rows, and 1 more variable: otrvab01 <dbl>
rownames(ddendvab12)<-ddendvab12$Name
rownames(ddendvab12)
## [1] "AMA" "ANC" "APU" "ARE" "AYA" "CAJ" "CUS" "HUAV" "HUAC" "ICA"
## [11] "JUN" "LLIB" "LAM" "LIM" "LORE" "MDD" "MOQ" "PAS" "PIU" "PUN"
## [21] "SMA" "TAC" "TUM" "UCA"
ddendvab12$Name <- NULL
ddendvab12
## # A tibble: 24 x 9
## agrvab12 minvab12 manvab12 convab12 comvab12 tycvab12 ryhvab12 sguvab12
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 33.2 0.316 8.41 13.3 8.72 8.43 2.72 12.8
## 2 7.30 26.2 12.2 7.49 7.60 8.74 2.55 6.85
## 3 24.0 0.542 8.12 17.1 11.9 3.12 4.20 20.7
## 4 12.4 8.64 17.3 13.9 14.5 8.51 2.87 3.99
## 5 18.8 10.2 7.69 17.5 12.9 4.07 2.20 14.7
## 6 18.9 20.0 11.3 8.47 10.5 4.54 3.01 9.61
## 7 10.3 20.1 7.98 17.1 11.5 5.88 6.23 6.96
## 8 14.0 8.07 3.02 2.14 7.36 2.00 1.47 12.6
## 9 23.7 3.10 9.70 4.08 15.9 13.0 4.79 13.4
## 10 16.4 8.02 20.2 13.5 10.8 8.05 3.56 4.84
## # ... with 14 more rows, and 1 more variable: otrvab12 <dbl>
Nótese que en nuestro caso particular no necesitamos estandarizar los datos, aunque dependiendo de las características de las observaciones a analizar cabría la posibilidad de que fuera necesario normalizarlos antes de realizar el análisis de conglomerados.
Medidas de distancia de los conglomerados: Distancia Euclídea
Una de las medidas más utilizadas para determinar el grado de similitud o disimilitud entre observaciones es la distancia euclídea (o distancia euclidiana), distancia que suele ser la que R nos muestra por defecto. No obstante téngase en cuenta que existen otro tipo de medidas alternativas para medir la distancia de las similitudes (o diferencias) entre observaciones como puede ser la distancia Manhattan, Canberra, binaria o la distancia en función del coeficiente de correlación de Pearson o de Kendall. La distancia euclídea en un espacio bidimensional, cuya formulación deriva del Teorema de Pitágoras, sería la distancia “ordinaria” entre dos puntos en un plano cartesiano o la longitud del segmento de recta que une dichos puntos. La formulación básica para un espacio de dos dimensiones puede ser fácilmente ajustada, como se observa en el link, para estimar la distancia euclídea entre diversos puntos en un espacio n-dimensional.
Del paquete {stats} podemos utilizar la función dist() para obtener la matriz de distancias. Como hemos indicado, la metodología que viene por defecto es la distancia euclídea, aunque podemos indicar otros métodos con el comando method= " ". De forma alternativa podemos utilizar la función get_dist() del paquete {factoextra}, que básicamente nos devuelve el mismo resultado. No obstante, este paquete incluye la función fviz_dist() que nos permite visualizar en un heat map dicha matriz de distancias, donde, por ejemplo, podemos indicar que nos muestre en color rojo las distancias mayores y el azul los valores más pequeños (más similitud). Veamos cómo sería su aplicación para el año 2001 y 2012:
2001:
vab01.dist <- dist(ddendvab01, method="euclidean") # del paquete {stats}
vab01.dist
## 1 2 3 4 5 6 7
## 2 41.621436
## 3 18.047724 36.185017
## 4 30.021817 24.691644 23.839064
## 5 16.554823 34.020496 6.208849 20.644736
## 6 38.047913 14.332659 34.005720 30.288998 32.085124
## 7 30.851679 20.917730 20.952008 10.474156 19.184760 24.754864
## 8 49.379983 43.214779 47.100719 39.618122 45.992290 50.113661 41.207654
## 9 14.563109 31.020545 14.663112 20.693440 10.938199 28.056333 19.119588
## 10 24.848530 26.108158 20.273682 6.549371 16.734286 29.903857 11.924584
## 11 29.334238 18.465444 23.634085 8.500016 20.830363 24.508864 9.068033
## 12 22.893482 24.703846 20.186675 9.910558 17.275019 27.946010 14.159531
## 13 32.690369 33.539146 25.417764 12.757188 22.224754 37.256568 16.005144
## 14 42.448918 32.213563 34.084953 16.365218 32.109701 41.657454 20.255644
## 15 27.189348 20.493740 19.207146 12.011300 16.362440 21.851088 6.107261
## 16 46.450165 15.954397 41.084850 35.150484 39.212873 12.379022 28.442434
## 17 47.218150 19.156303 42.258384 28.258812 39.696971 27.257923 28.964831
## 18 66.013294 34.819854 61.760574 57.013411 60.325105 29.321506 50.853216
## 19 32.195628 24.790691 24.294134 5.051201 21.270858 30.443947 10.386381
## 20 25.675252 20.727531 18.858357 11.005873 16.059123 24.051961 8.339680
## 21 15.439033 33.778222 9.924107 17.194065 8.041998 33.528965 17.732080
## 22 39.722017 14.264120 32.032396 19.593611 30.039355 21.113580 13.973553
## 23 28.742797 33.251174 21.188740 17.402234 19.877540 37.069366 16.717167
## 24 22.030579 30.353435 15.950262 11.094928 12.141822 31.568806 12.726203
## 8 9 10 11 12 13 14
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9 47.048697
## 10 42.048680 16.144614
## 11 36.095063 19.217288 10.342334
## 12 40.163578 16.505921 6.449034 10.387561
## 13 42.156697 22.843906 15.634843 17.558267 20.305233
## 14 34.813952 33.994612 21.006789 19.330544 24.120915 17.941590
## 15 40.619487 14.991482 11.834205 8.961090 13.176571 16.932385 23.839085
## 16 50.431473 34.817442 35.966427 28.789788 35.350279 40.157842 42.807043
## 17 52.457086 38.836908 28.994715 26.874964 27.862574 39.459878 35.569798
## 18 67.954982 56.019331 57.964166 50.900427 56.444247 62.463870 64.637755
## 19 43.075359 22.311453 8.033659 11.312785 12.203479 14.361582 17.071826
## 20 38.277337 14.581673 10.302703 5.896250 11.005102 17.345279 22.282908
## 21 43.218611 11.504922 12.981533 18.367636 12.901536 20.004977 28.837183
## 22 40.847136 27.069512 22.530284 14.083049 23.551998 23.739723 24.908054
## 23 38.018821 20.104451 17.831510 17.013759 20.702621 13.985636 20.510373
## 24 43.346306 12.674225 7.833849 14.373009 11.660680 12.989976 23.630000
## 15 16 17 18 19 20 21
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16 26.501404
## 17 29.805982 32.249749
## 18 49.036852 23.603647 46.123421
## 19 12.948940 35.288888 26.240050 56.892871
## 20 6.363470 28.741118 29.904652 51.258910 13.007432
## 21 15.929019 40.678226 38.987677 62.303962 18.872831 14.899666
## 22 14.997788 19.701881 29.010656 41.589042 20.374433 15.514851 29.461432
## 23 17.482562 39.391362 42.544815 62.279761 19.881574 14.575890 17.606908
## 24 11.334939 37.332937 35.250792 59.674767 12.356784 11.842025 9.025217
## 22 23
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17
## 18
## 19
## 20
## 21
## 22
## 23 23.104300
## 24 24.607014 15.527966
fviz_dist(vab01.dist, gradient = list(low = "blue", mid = "white", high = "red"))
2012:
vab12.dist <- dist(ddendvab12, method="euclidean")
vab12.dist
## 1 2 3 4 5 6 7
## 2 38.725104
## 3 14.334401 37.535336
## 4 26.857734 21.551730 25.920878
## 5 19.066865 26.573035 12.884694 17.992101
## 6 25.536046 16.281142 25.105195 17.852965 15.054203
## 7 31.486403 15.626975 28.023304 16.821915 15.999396 13.440683
## 8 44.774473 36.918034 45.097799 38.697638 41.680021 39.746629 41.763707
## 9 16.124127 32.073449 18.734152 21.374924 18.877377 21.189728 27.491624
## 10 23.492220 23.938052 23.864184 7.219435 17.622811 17.113385 19.047795
## 11 25.700331 18.587843 25.881540 9.926721 18.072184 16.213197 17.152572
## 12 22.428204 23.388767 25.269587 11.276278 19.951904 15.868357 21.943771
## 13 32.747540 31.540200 30.595265 17.426478 26.003181 28.862556 27.510768
## 14 39.632725 31.037112 38.021719 20.564793 33.628855 33.438212 32.175848
## 15 23.533469 26.423031 20.532698 12.996390 16.931608 19.884982 21.608641
## 16 38.911172 12.204969 36.948438 27.274949 26.757485 16.631138 17.876028
## 17 36.977947 17.503881 33.822161 16.720449 23.970663 20.473819 16.273393
## 18 51.361382 21.660365 49.858966 39.905884 38.363543 27.545255 27.400714
## 19 26.541951 24.839544 25.416345 6.653681 19.893671 19.983088 21.420017
## 20 20.586878 24.131724 20.582768 12.462531 16.056465 17.868064 20.887060
## 21 10.847204 34.411009 15.123829 20.482051 17.935366 22.212056 28.633616
## 22 32.545156 17.768325 30.910533 14.278362 22.373274 20.296460 17.551315
## 23 27.752252 30.896048 26.267661 21.018436 23.724162 28.395836 27.371578
## 24 21.448732 29.517013 21.235467 15.016512 19.092320 21.516910 24.745267
## 8 9 10 11 12 13 14
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9 41.703660
## 10 41.947093 20.173292
## 11 31.776615 18.163288 13.946674
## 12 38.582729 18.824252 7.223533 13.673173
## 13 39.091376 22.098589 22.699841 16.719344 24.603350
## 14 32.856604 29.922962 25.633717 19.312619 26.019944 14.864424
## 15 35.973120 13.412901 15.285133 11.100172 16.088870 13.384605 19.191752
## 16 38.823920 30.557894 29.532973 22.207632 28.549808 32.929429 35.356501
## 17 43.118309 34.324728 17.443193 21.440476 20.576887 31.961624 31.349928
## 18 50.268823 46.376409 41.524276 37.225689 40.887085 48.320982 50.706028
## 19 38.319160 18.608840 9.559636 11.173756 11.434262 14.382754 17.610644
## 20 33.632862 12.255512 14.056621 7.283433 13.565022 16.542188 21.018405
## 21 40.090399 11.276158 17.657693 19.870088 15.802203 25.415284 31.016718
## 22 34.226916 22.529212 19.612236 8.588378 20.751362 15.581064 18.202000
## 23 34.667514 18.668526 24.495597 15.313445 25.497121 15.233205 20.320676
## 24 36.630817 11.256488 16.455548 13.055795 16.067915 13.884774 20.611739
## 15 16 17 18 19 20 21
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16 27.210728
## 17 26.504216 27.020757
## 18 43.614447 18.783651 33.440442
## 19 9.389435 29.060926 21.613348 43.298766
## 20 7.333431 26.020549 25.377114 41.913059 11.128392
## 21 15.333563 35.131506 32.671148 49.364225 18.142915 14.298540
## 22 14.395399 20.262738 23.283441 36.001702 15.358820 13.257151 26.876449
## 23 14.078221 31.373448 33.477315 48.258162 19.711153 12.670341 23.374268
## 24 5.617363 29.912718 30.034845 46.094571 10.836893 8.764581 12.644114
## 22 23
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9
## 10
## 11
## 12
## 13
## 14
## 15
## 16
## 17
## 18
## 19
## 20
## 21
## 22
## 23 14.912244
## 24 17.489030 15.500177
fviz_dist(vab12.dist, gradient = list(low = "blue", mid = "white", high = "red"))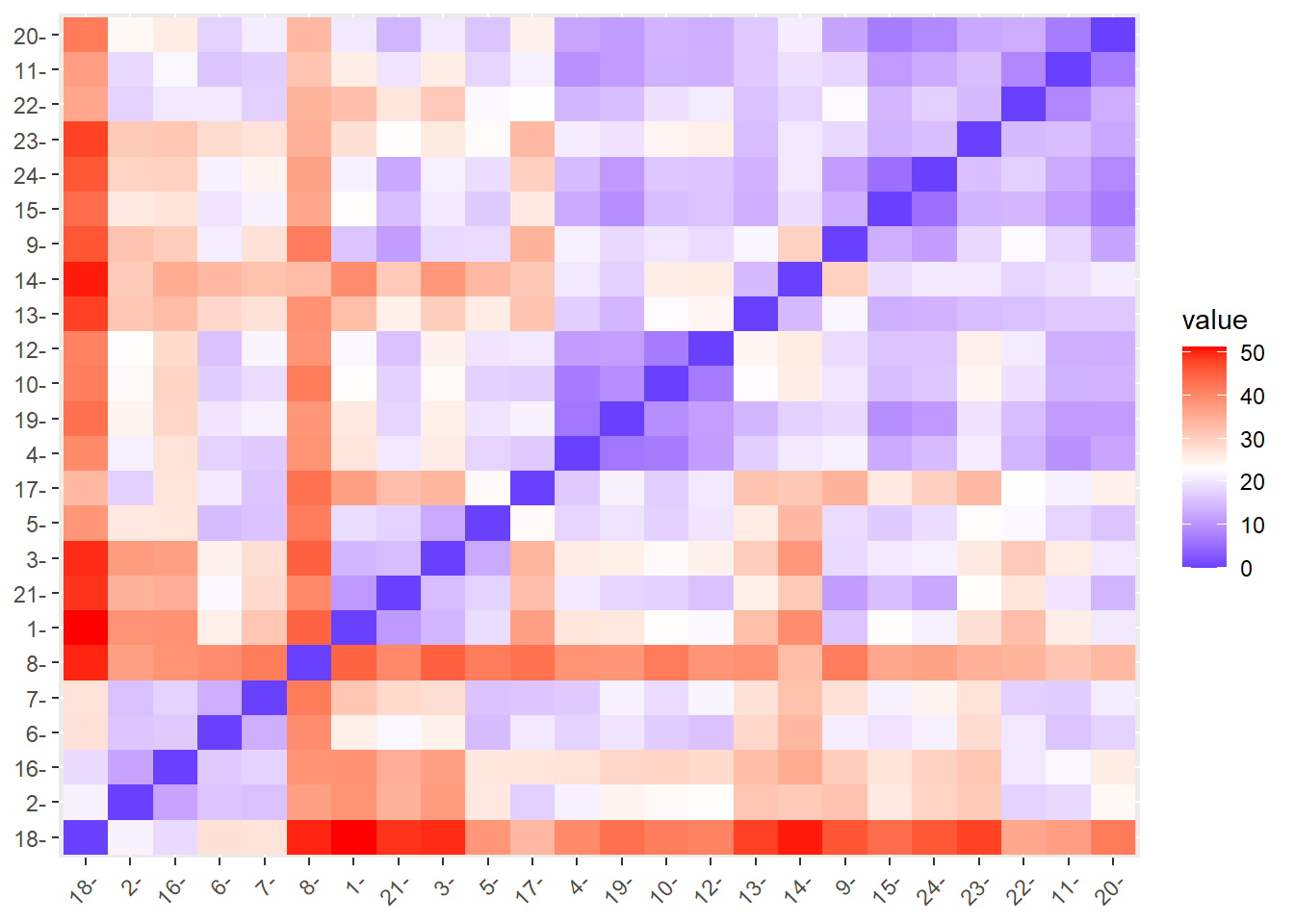
Método de agrupamiento:
Una vez tenemos estimadas las distancias, según el método escogido, un segundo elemento a considerar es cómo medir las diferencias entre los grupos de observaciones o conglomerados. De nuevo, existen diversas propuestas para llevar a cabo este proceso y, dependiendo del criterio escogido las agrupaciones obtenidas, y el dendrograma resultante, mostrará diferencias significativas. Por tanto, no podemos hablar de una solución óptima, sino que la metodología escogida dependerá del carácter de los datos, del investigador y de su criterio. Los métodos más utilizados son los siguientes:
- Distancia mínima (máxima similitud) o single linkage: La distancia según este criterio vendría dada por la mínima distancia entre los distintos componentes.
- Distancia máxima (mínima similitud) o complete linkage: La distancia según este criterio vendría dada por la máxima distancia entre los distintos componentes.
- Distancia promedio o average linkage: La distancia según este criterio vendría dada por el promedio de las distancias de los componentes de un conglomerado con respecto al promedio de las distancias del otro grupo.
- En base los centroides o centroid linkage: La distancia según este criterio vendría dada por la mayor semejanza entre los centroides de los clusters.
- Método Ward (mínima varianza): La distancia según este criterio vendría dada por el menor incremento en el valor total de la suma de los cuadrados de las diferencias existentes, dentro de cada conglomerado, de cada observación con respecto al centroide del cluster.
Para evitar ser excesivamente repetitivos en los siguientes apartados vamos a mostrar cómo realizar el proceso siguiendo el procedimiento de agrupación según la distancia promedio (average linkage) y según el método Ward. Podremos de esta forma comprobar las diferencias en los resultados obtenido dependiendo del criterio escogido.
Average linkage:
2001
Para llevar a cabo la agrupación de conglomerados jerárquicos utilizamos la función hclust() del paquete {stats}.
HCvab01<- hclust(vab01.dist, method="average")
HCvab01
##
## Call:
## hclust(d = vab01.dist, method = "average")
##
## Cluster method : average
## Distance : euclidean
## Number of objects: 24
Una vez hemos realizado la agrupación podemos representar dichos conglomerados en un dendrograma. Para ello tenemos diversas posibilidades utilizando la función plot() del paquete {graphics}, obteniendo dendrogramas que muestran ligeras diferencias, o con otros paquetes de R como {factoextra}:
Opción 1.
plot(HCvab01)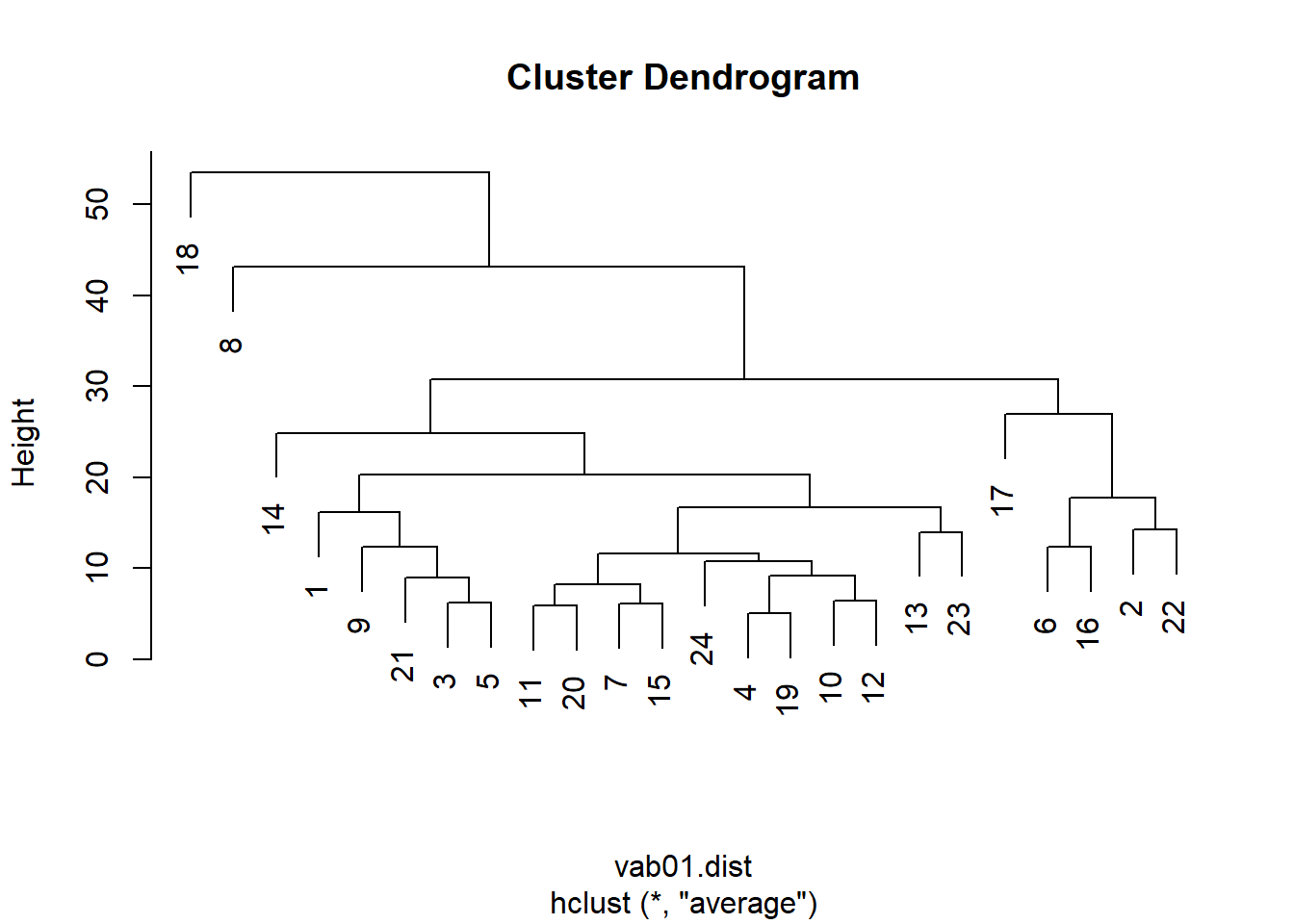
Opción 2.
plot(HCvab01, hang= -1, cex=0.6)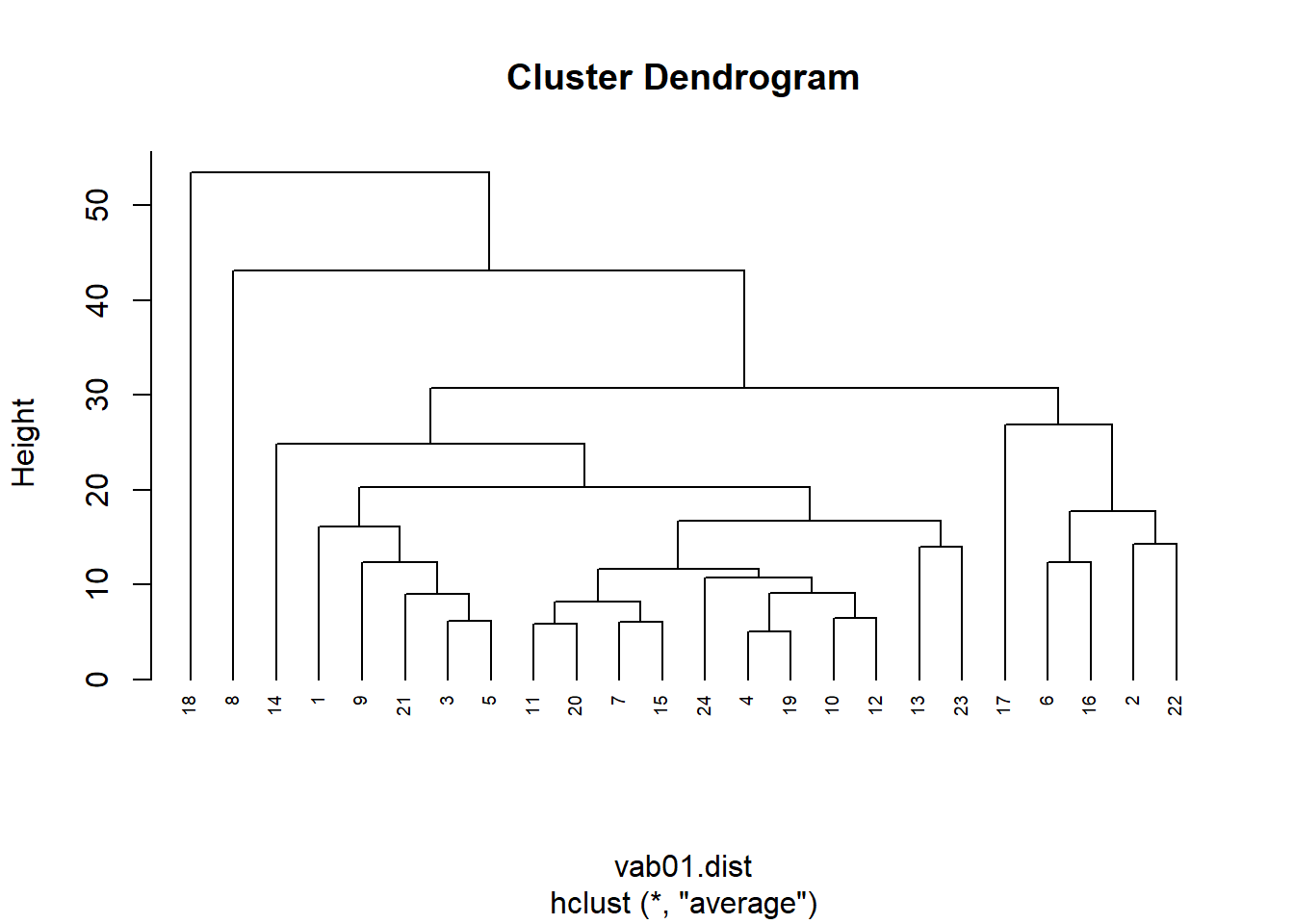
Opción 3.
DNDvab01<- as.dendrogram(HCvab01)
DNDvab01
## 'dendrogram' with 2 branches and 24 members total, at height 53.44587
plot(DNDvab01,
main= "Dendrograma VAB de las regiones peruanas, 2001",
sub= "Método Average") 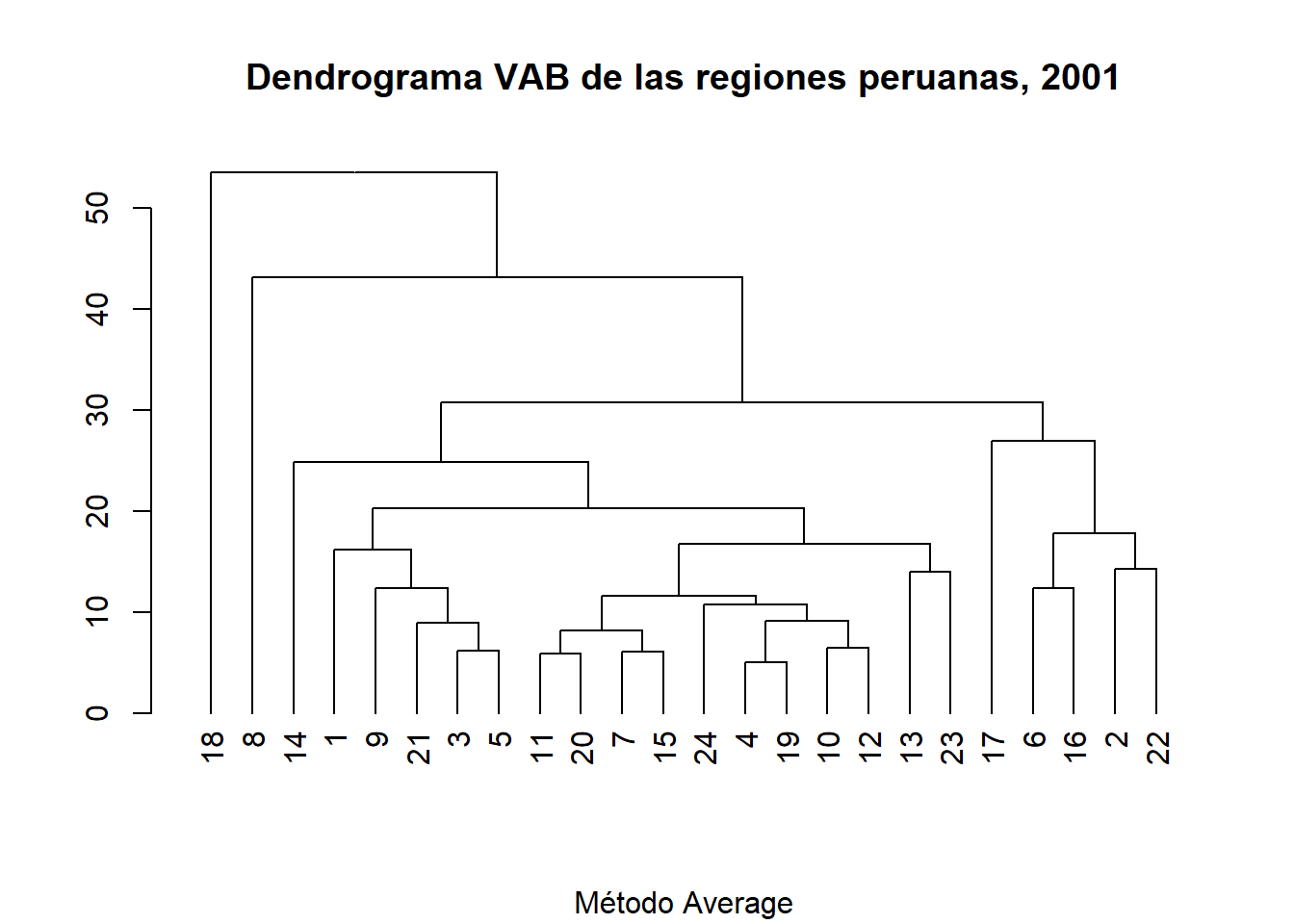
Opción 4.
DNDvab01_2<-fviz_dend(DNDvab01, cex=0.5)
DNDvab01_2 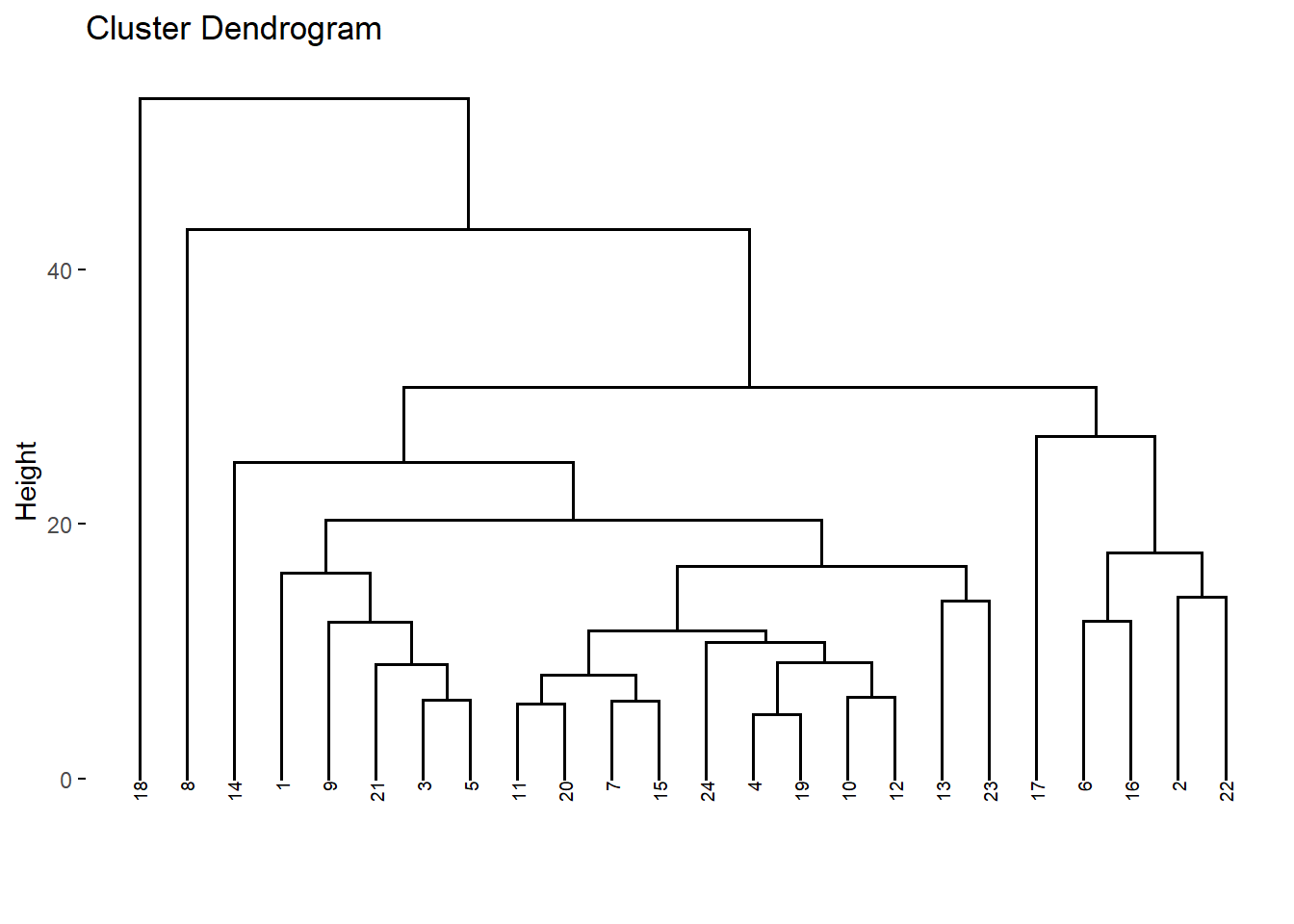
Opción 5.
fviz_dend(DNDvab01, cex=0.5, horiz=TRUE) 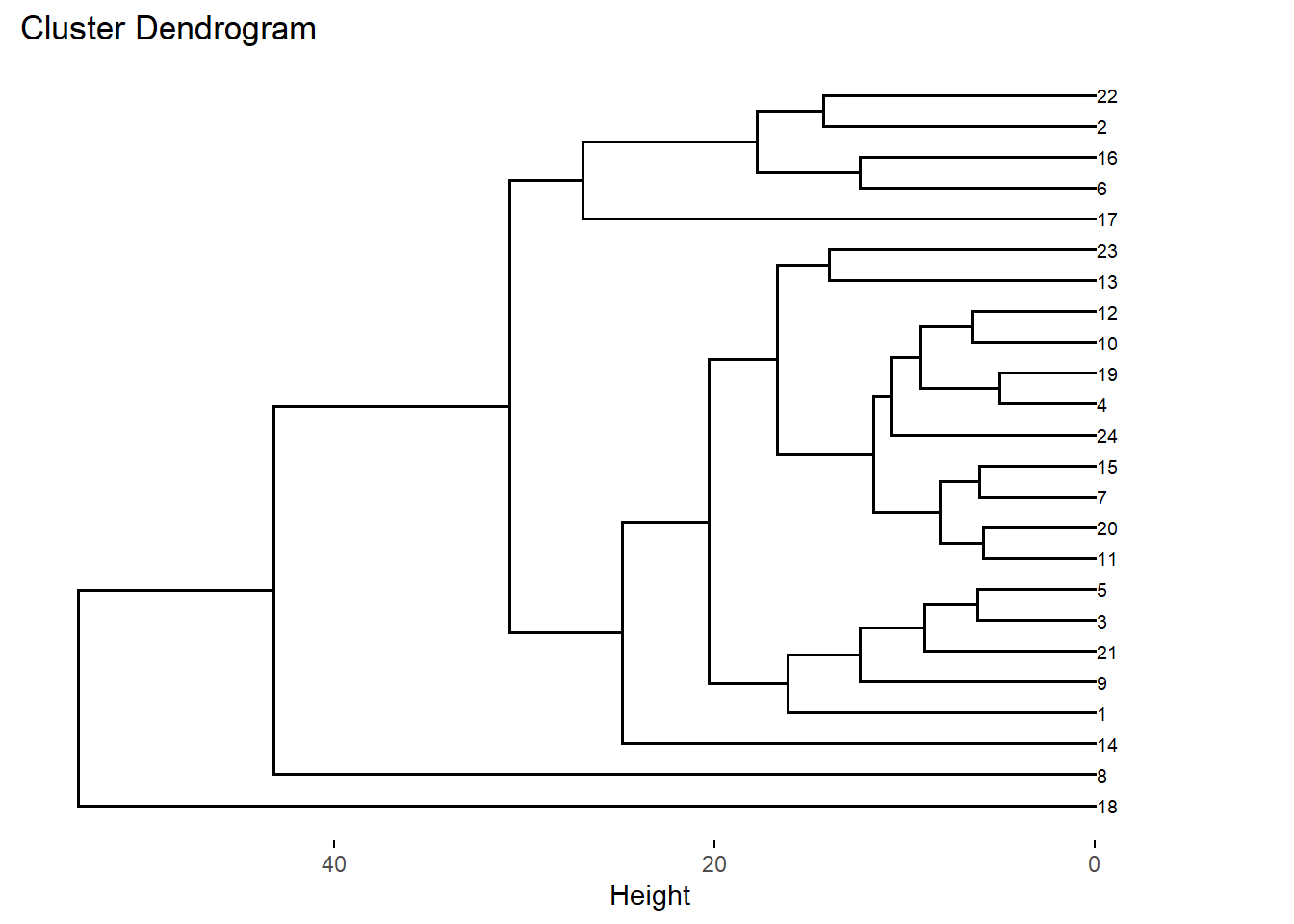
2012
Para el año 2012 el Análisis de Conglomerados Jerárquico utilizando el método de distancia promedio (average linkage) y su correspondiente dendrograma sería el siguiente:
HCvab12<- hclust(vab12.dist, method="average")
DNDvab12<- as.dendrogram(HCvab12)
DNDvab12
## 'dendrogram' with 2 branches and 24 members total, at height 39.14731
plot(DNDvab12,
main= "Dendrograma VAB de las regiones peruanas, 2012",
sub= "Método Average") 
Método de Ward:
Para realizar un dendrograma utilizando otro método de agrupamiento únicamente debemos seleccionar el criterio escogido. la función hclust() permite escoger entre: “ward.D”, “ward.D2”, “single”, “complete”, “average”, “mcquitty”, “median” o “centroid”. Para realizar el análisis aplicando, por ejemplo, el método Ward indicaremos method= "ward.D2" en la funciónhclust()` (véase: Murtagh, F., & Legendre, P. 2014. Ward’s hierarchical agglomerative clustering method: which algorithms implement Ward’s criterion?. Journal of Classification, 31/3, 274-295)
2001
HCvab01b<-hclust(vab01.dist, method="ward.D2")
DNDvab01b<- as.dendrogram(HCvab01b)
DNDvab01b
## 'dendrogram' with 2 branches and 24 members total, at height 91.3892
plot(DNDvab01b,
main= "Dendrograma VAB de las regiones peruanas, 2001",
sub= "Método Ward") 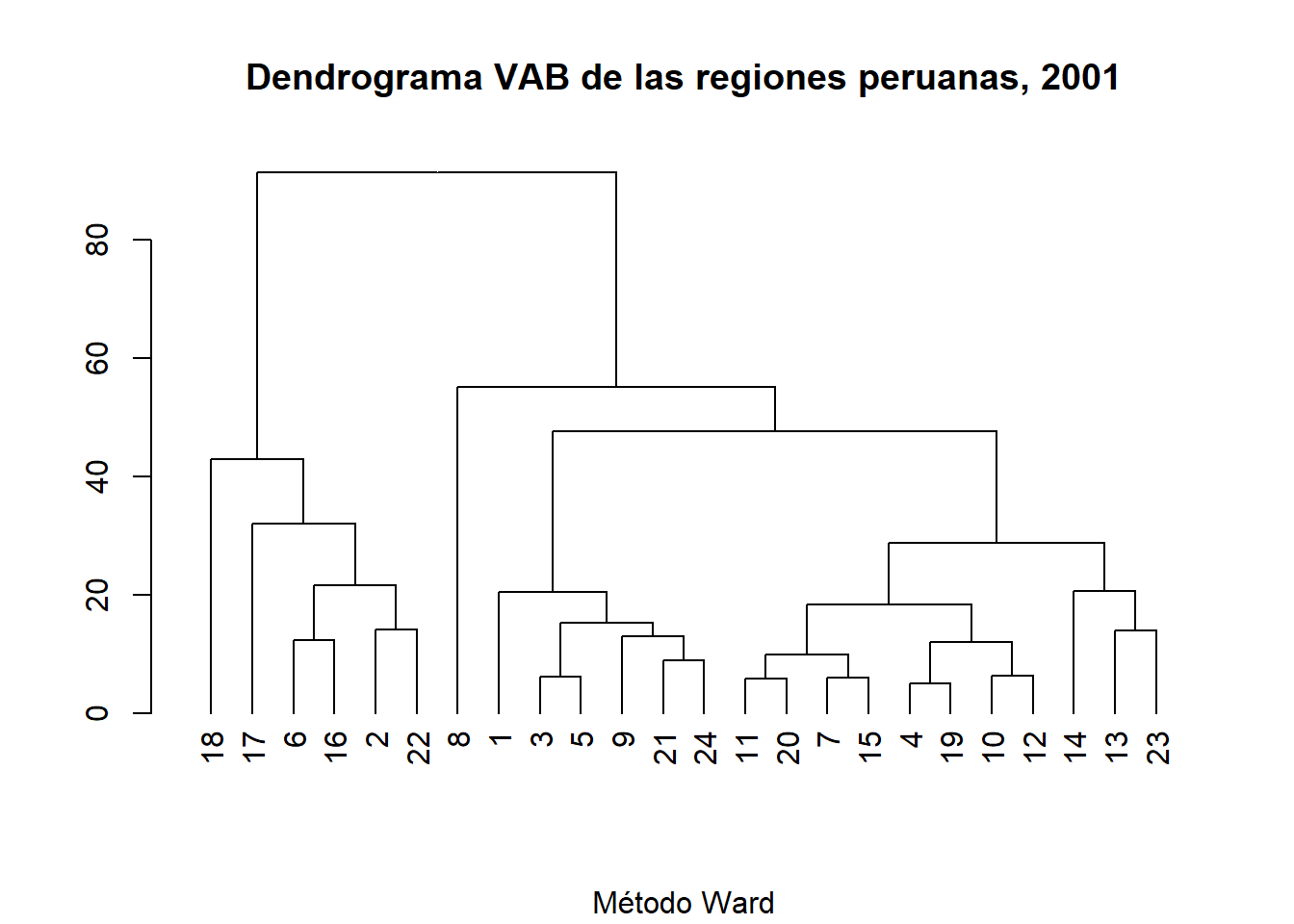
2012
HCvab12b<-hclust(vab12.dist, method="ward.D2")
DNDvab12b<- as.dendrogram(HCvab12b)
DNDvab12b
## 'dendrogram' with 2 branches and 24 members total, at height 67.22437
plot(DNDvab12b,
main= "Dendrograma VAB de las regiones peruanas, 2012",
sub= "Método Ward") 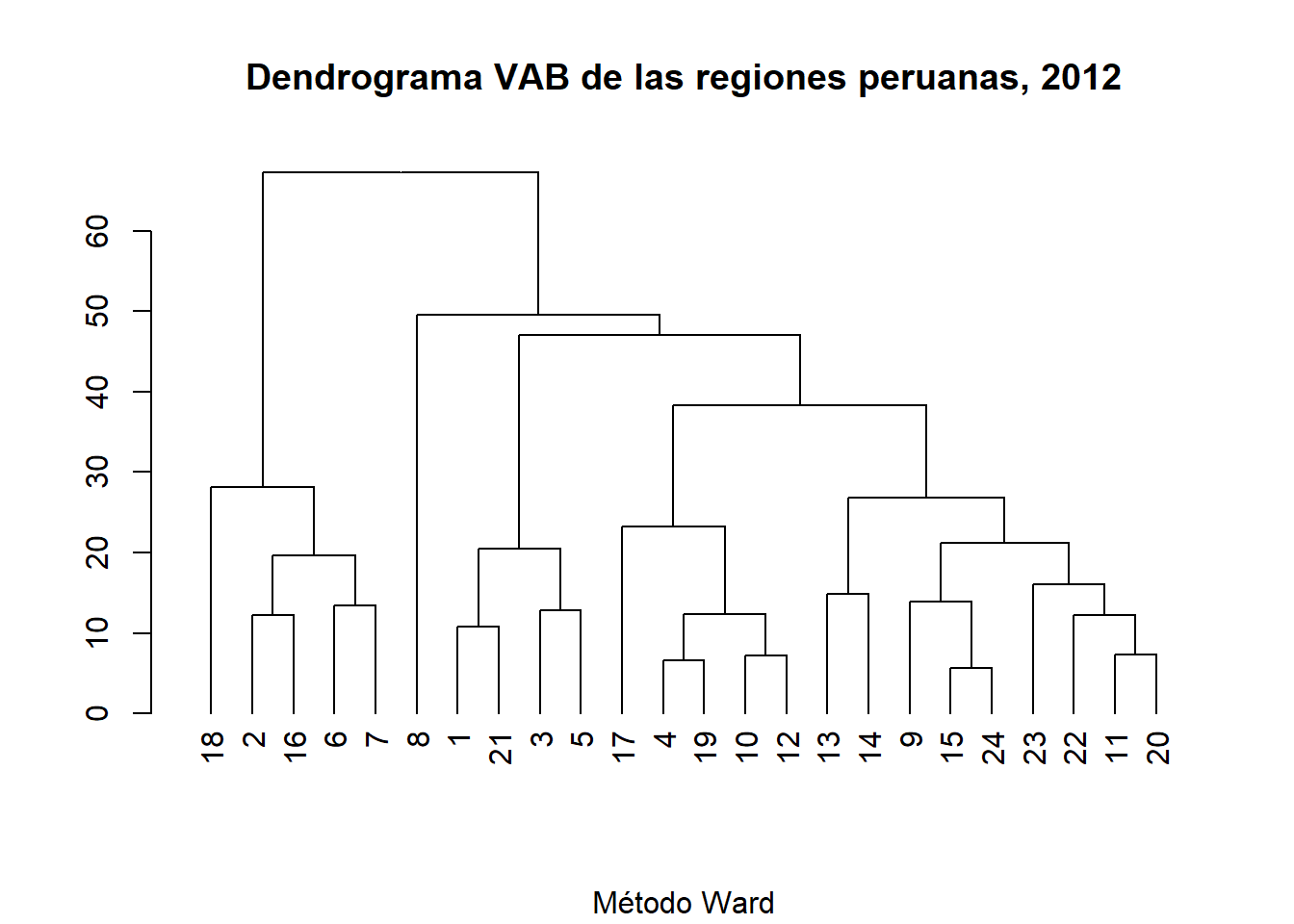
Comparación entre dendrogramas
Con el paquete {dendextend} podemos visualizar y comparar dendrogramas de conglomerados jerárquicos. La comparación visual se realiza utilizando la función tanglegram(), que sitúa los dendrogramas que queremos comparar uno enfrente del otro y conecta sus observaciones mediante líneas. En nuestro ejercicio, de nuevo por motivos de simplicidad, vamos a utilizar únicamente los dendrogramas de 2001 y 2012 estimados con el criterio de agrupamiento de promedios.
VAB 2001 vs VAB 2012
En primer lugar creamos una lista con los dendrogramas DNDvab01 y DNDvab12 que denominaremos dend_listvab.
#creamos una lista con los dos dendrograms VAB 01 Y 12 (Average)
dend_listvab<- dendlist(DNDvab01,DNDvab12)
dend_listvab
## [[1]]
## 'dendrogram' with 2 branches and 24 members total, at height 53.44587
##
## [[2]]
## 'dendrogram' with 2 branches and 24 members total, at height 39.14731
##
## attr(,"class")
## [1] "dendlist"
A la hora de comparar los dendrogramas podemos escoger entre distintas posibles clasificaciones utilizando la función untangle(). Las opciones a escoger son las siguientes: “labels”, “ladderize”, “random”, “step1side”, “step2side”, “DendSer”. Veamos gráficamente la diferencia entre algunas de ellas:
method = “labels”
dendlist(dend_listvab) %>%
untangle(method = "labels") %>%
tanglegram(sub= "Method = labels",
main_left= "VAB 2001",
main_right = "VAB 2012",
cex_sub=1)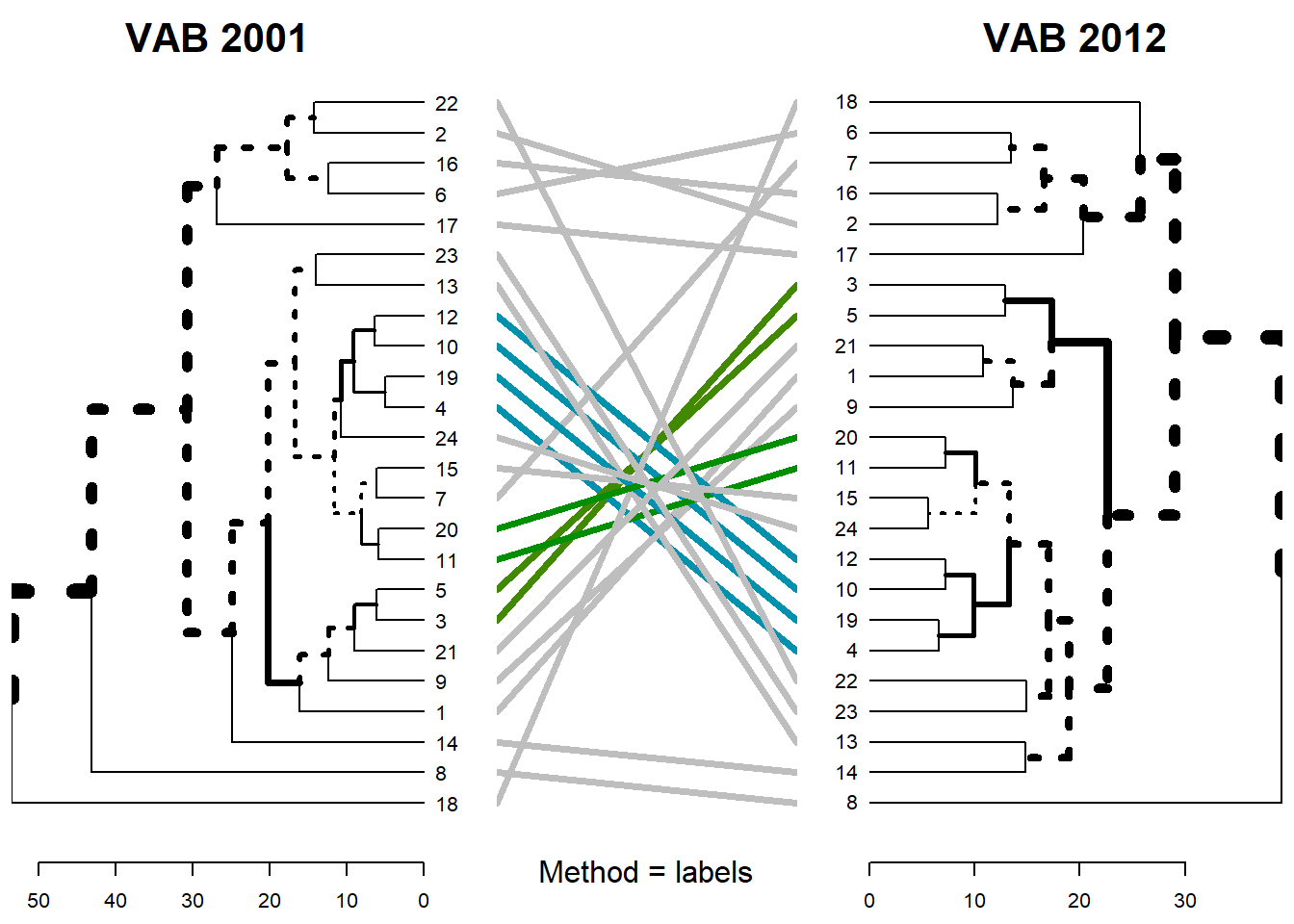
method = “step1side”
dendlist(dend_listvab) %>%
untangle(method ="step1side") %>%
tanglegram(sub= "Method = step1side",
main_left= "VAB 2001",
main_right = "VAB 2012",
cex_sub=1)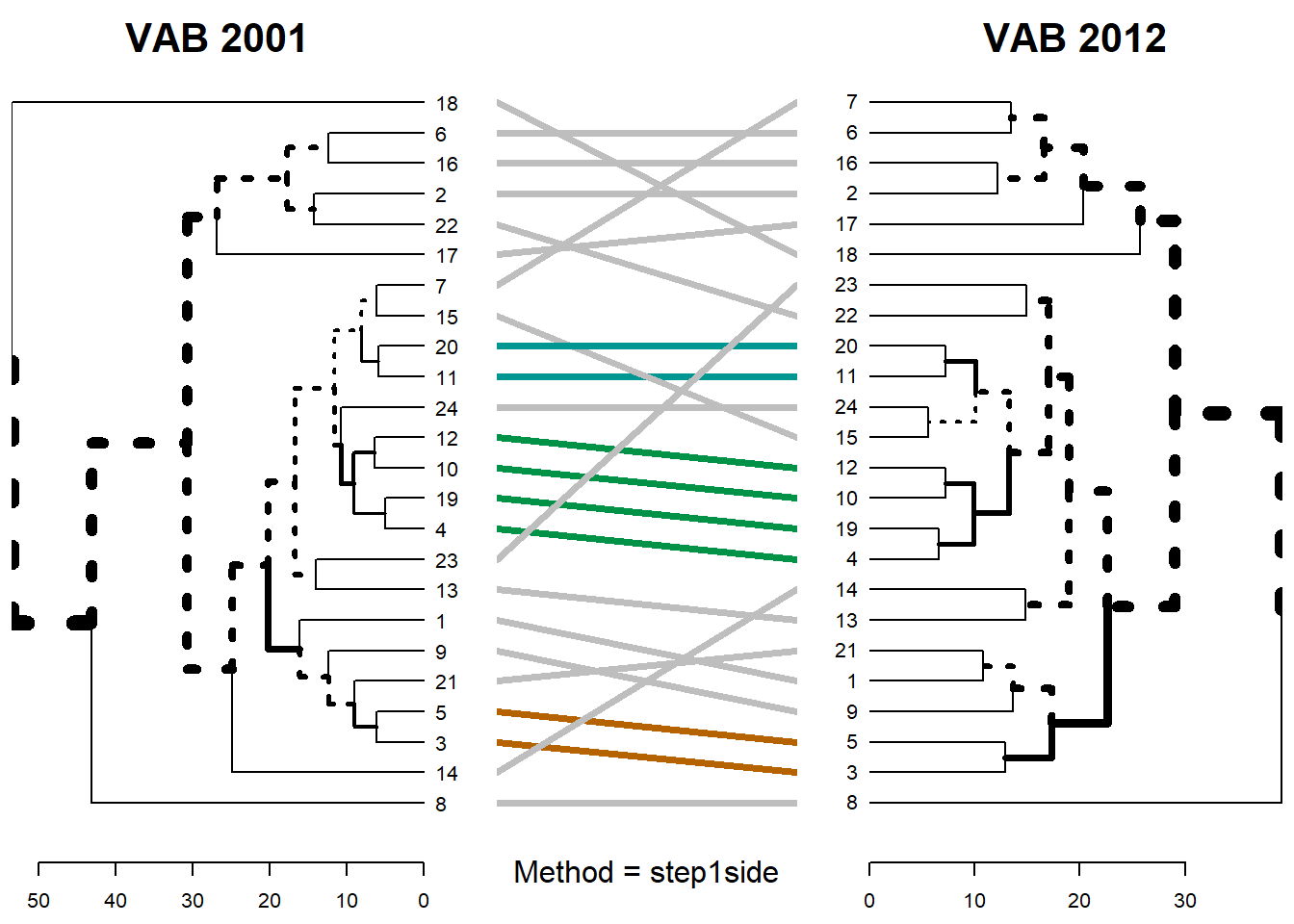
method = “ladderize”
dendlist(dend_listvab) %>%
untangle(method ="ladderize") %>%
tanglegram(sub= "Method = ladderize",
main_left= "VAB 2001",
main_right = "VAB 2012",
cex_sub=1)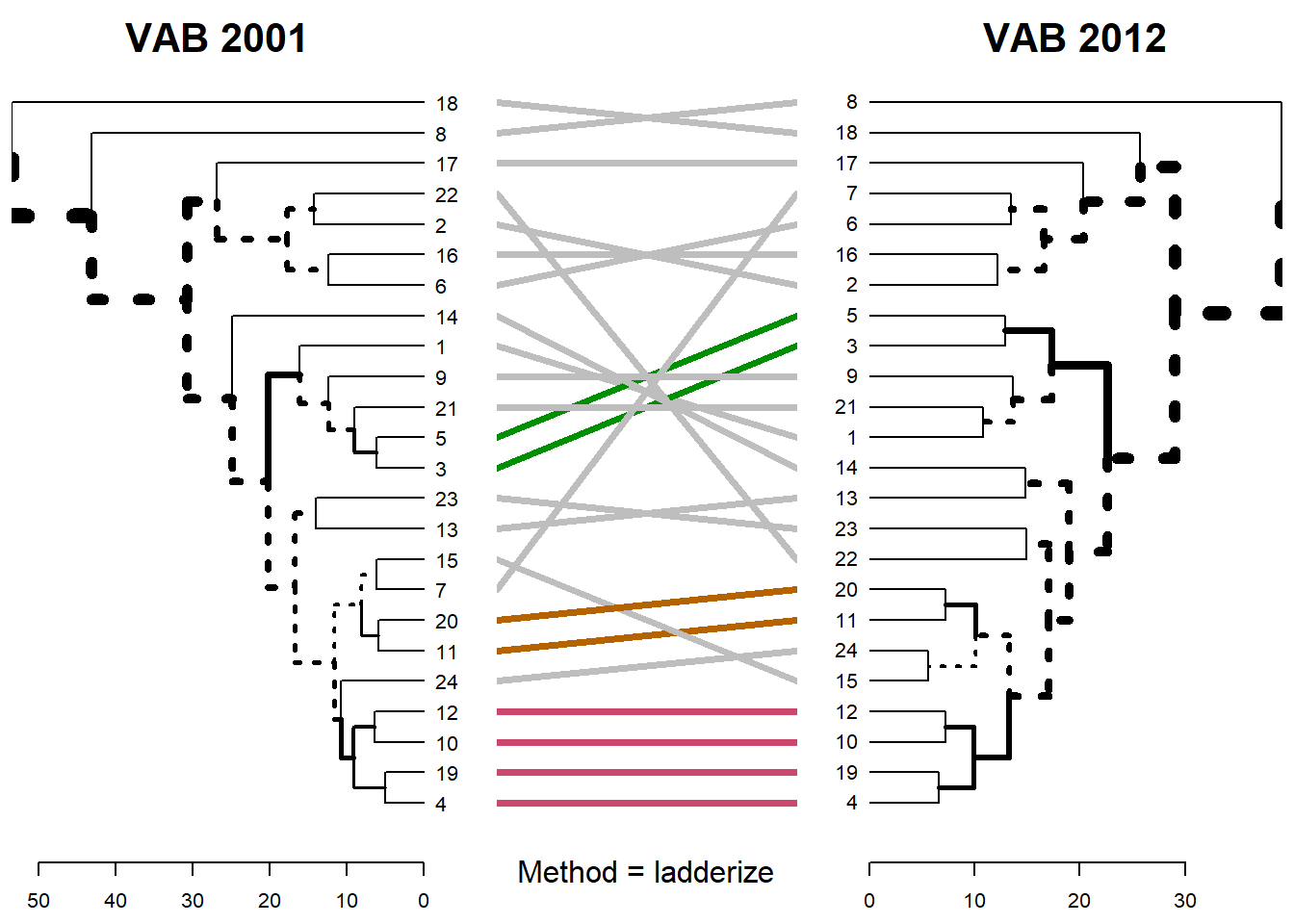
customizado
Existen diversas opciones para customizar el tanglegram que se pueden consultar en la documentación del paquete {tanglegram}. Adicionalmente, con la función entanglement() podemos indicar la fortaleza del entrelazamiento o enredo (entanglement) de los dos dendragramas. El entanglement corresponde a una medida entre 1 (entrelazamiento/enredo fuerte o completo) y 0 (no entrelazamiento/enredo). Por consiguiente, un valor más cercano a 0 será indicativo de que entre los dos dendrogramas existe una mayor correspondencia que si el resultado fuera mayor.
tanglegram(DNDvab01,DNDvab12,
sort=T,
main_left= "VAB 2001",
main_right = "VAB 2012",
common_subtrees_color_lines = FALSE,
common_subtrees_color_branches = TRUE,
sub = paste("entanglement =", round(entanglement(dend_listvab), 2)),
cex_sub=1,
fast=TRUE)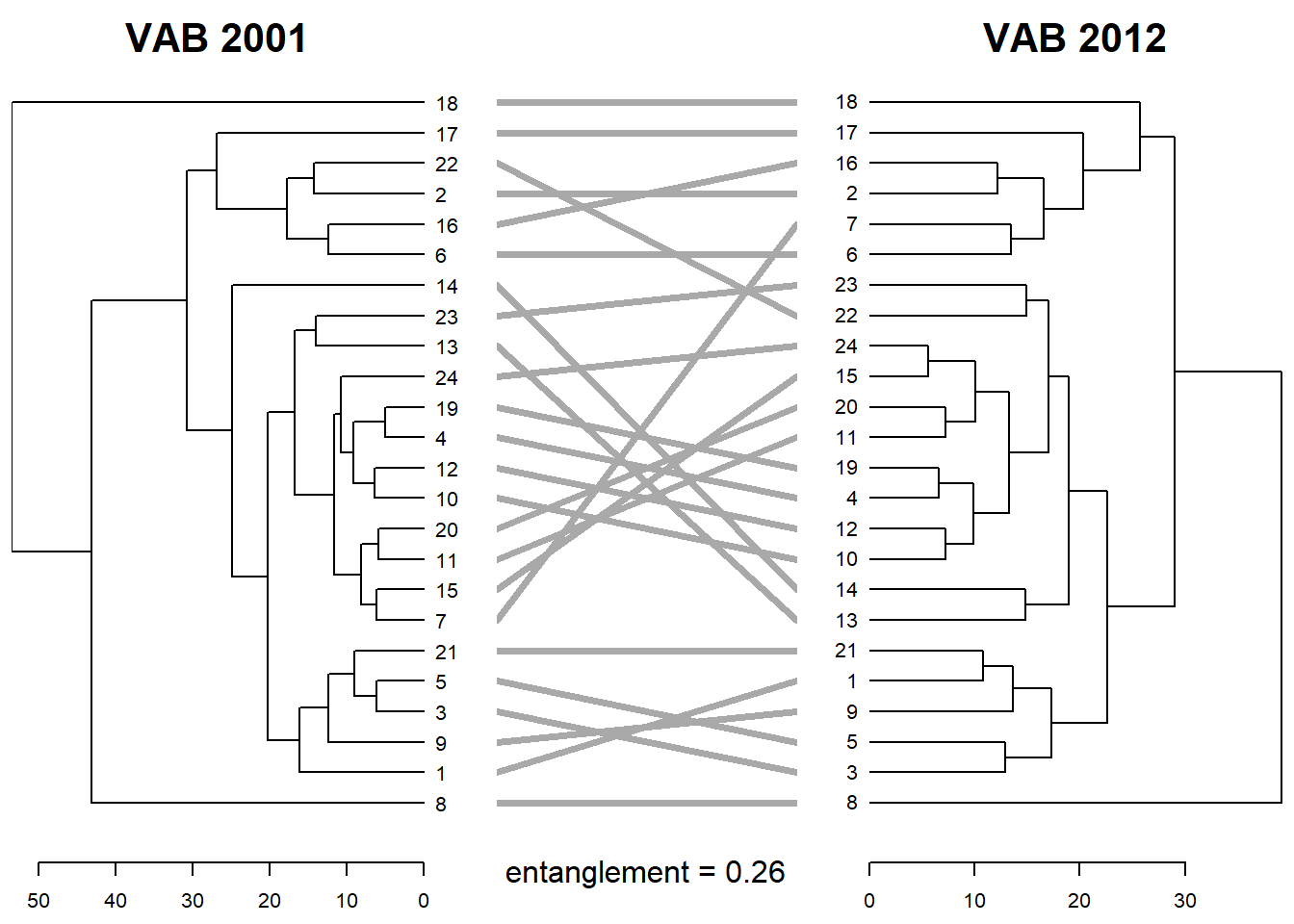
Average vs. Ward
De forma similar podemos comparar el dendrograma realizado siguiendo el criterio de clasificación según la distancia promedio y dendrograma realizado según el criterio Ward de mínima varianza. El procedimiento sería similar al realizado en el punto previo.
#creamos una lista con los dos dendrograms (Average y Ward) para el año 2001
dend_listvabb<- dendlist(DNDvab01,DNDvab01b)
dend_listvabb
## [[1]]
## 'dendrogram' with 2 branches and 24 members total, at height 53.44587
##
## [[2]]
## 'dendrogram' with 2 branches and 24 members total, at height 91.3892
##
## attr(,"class")
## [1] "dendlist"
tanglegram(DNDvab01,DNDvab01b,
sort=T,
main_left= "Average",
main_right = "Ward",
highlight_distinct_edges = T,
common_subtrees_color_lines = FALSE,
common_subtrees_color_branches = TRUE,
sub = paste("entanglement =", round(entanglement(dend_listvabb), 2)),
cex_sub=1,
fast=TRUE)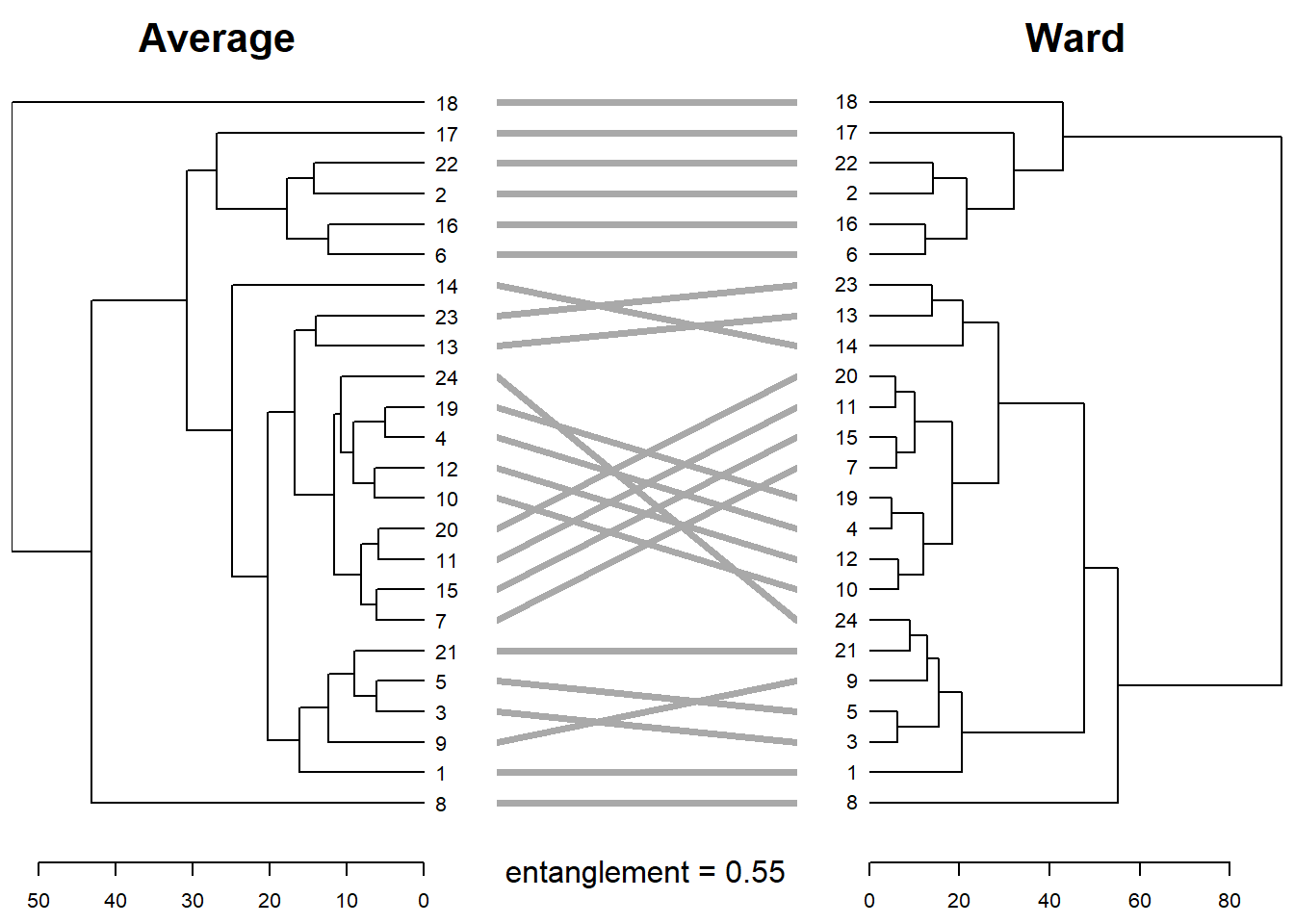
Correlación matrix entre dendogramas
Para obtener las matrices de correlación de los dendrogramas podemos hacer uso de la función cor.dendlist() del paquete {dendextend}. Esta función ofrece la posibilidad de escoger diversos coeficientes de correlación: “cophenetic” (viene establecido por defecto), “baker”, “common_nodes” o “FM_index”.
Correlación cofenética (Cophenetic)
Como hemos enunciado, para obtener la matriz de correlación cofenética podemos utilizar la función cor.dendlist(). Las matrices de correlación para los conglomerados de 2001 vs. 2012 (average) y para los modelos Average vs. Ward en 2001 serían, por consiguiente, las siguientes:
cor.dendlist(dend_listvab, method = "cophenetic") #average 2001 vs average 2012
## [,1] [,2]
## [1,] 1.0000000 0.6854301
## [2,] 0.6854301 1.0000000
cor.dendlist(dend_listvabb, method= "cophenetic") #average vs ward en 2001
## [,1] [,2]
## [1,] 1.0000000 0.6865269
## [2,] 0.6865269 1.0000000
Los coeficiente de correlación se podrían obtener con la función cor_cophenetic():
cor_cophenetic(DNDvab01, DNDvab12)
## [1] 0.6854301
cor_cophenetic(DNDvab01, DNDvab01b)
## [1] 0.6865269
Correlación Baker
Para estimar las matrices de correlación de Baker y sus correspondientes coeficientes de correlación seguiríamos un procedimiento similar.
cor.dendlist(dend_listvab, method = "baker")
## [,1] [,2]
## [1,] 1.0000000 0.7024245
## [2,] 0.7024245 1.0000000
cor.dendlist(dend_listvabb, method = "baker")
## [,1] [,2]
## [1,] 1.0000000 0.8126997
## [2,] 0.8126997 1.0000000
En este caso los coeficientes de correlación se obtendrían con la función cor_bakers_gamma():
cor_bakers_gamma(DNDvab01, DNDvab12)
## [1] 0.7024245
cor_bakers_gamma(DNDvab01, DNDvab01b)
## [1] 0.8126997
Grupos de clusters o conglomerados
El objetivo fundamental del análisis de conglomerados jerárquico consiste en establecer grupos de conglomerados con características similares de acuerdo a algún patrón determinado. Para representar gráficamente dichos conglomerados podemos utilizar la función fviz_dend() del paquete {factoextra}, el cual nos permite utilizar el lenguaje tradicional del paquete {ggplot2}. En nuestro caso particular utilizaremos un theme realizado por traffordDataLab, theme_lab(), que ya hemos utilizado en post previos y que encontramos muy agradable a la vista. Este theme lo cargamos con el siguiente comando:
source("https://github.com/traffordDataLab/assets/raw/master/theme/ggplot2/theme_lab.R")
Año 2001
Supongamos que para el año 2001 queremos clasificar el grupo de regiones peruanas en seis clusters con características similares (en este caso utilizamos el criterio de los promedios que viene por defecto). Para ello indicaremos k=6, correspondiente al número de conglomerados, e indicamos el color que queremos utilizar para diferenciarlos gráficamente en nuestro dendrograma.
fviz_dend(DNDvab01, k = 6,
cex = 0.7,
k_colors = c("grey40", "grey40", "grey40", "grey40","grey40", "grey40"),
color_labels_by_k = TRUE,
rect = TRUE,
rect_border = c("grey30", "grey70","darkgoldenrod1"," darkorange1","firebrick2", "darkmagenta"),
rect_fill = TRUE)+
labs(title = "Dendrograma VAB regional Perú, 2001",
subtitle = "(K = 6)",
caption = NULL,
x = NULL,
y = NULL,
fill = NULL) +
xlab(NULL)+
ylab(NULL)+
theme_lab()+
theme(panel.grid.major.x = element_blank(),
legend.position = "right")
## Warning in if (color == "cluster") color <- "default": la condición tiene
## longitud > 1 y sólo el primer elemento será usado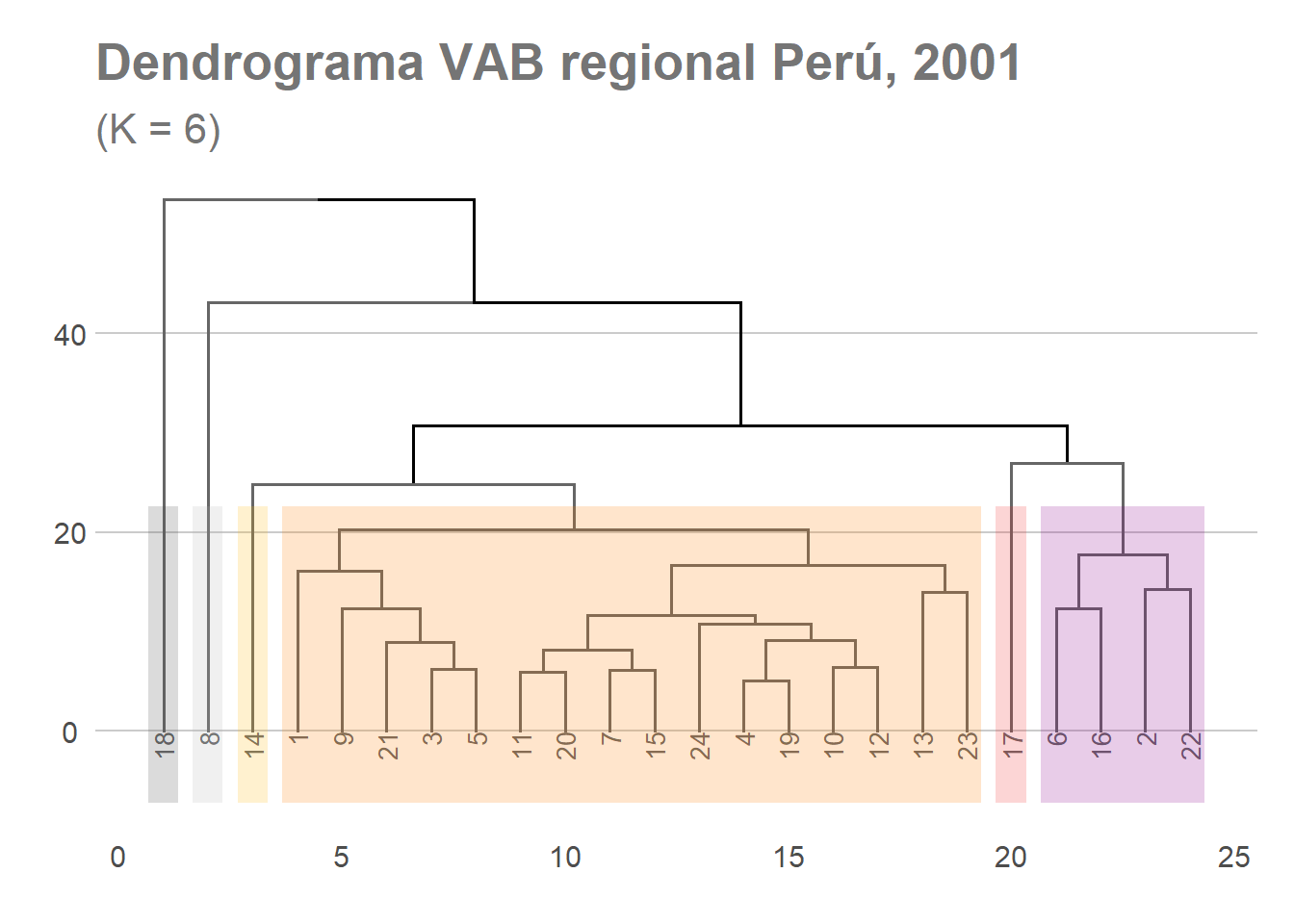
Año 2012
Pongamos que para el año 2012 queremos identificar cuatro grandes grupos de conglomerados. Para ello modificamos ligeramente el código anterior y obtenemos el siguiente dendrogama:
fviz_dend(DNDvab12, k = 4,
cex = 0.7,
k_colors = c("grey40", "grey40","grey40", "grey40"),
color_labels_by_k = TRUE,
rect = TRUE, # Add rectangle around groups
rect_border = c(" darkorange1","darkgoldenrod1","firebrick2", "darkmagenta"),
rect_fill = TRUE)+
labs(title = "Dendrograma VAB regional Perú, 2012",
subtitle = "(K = 4)",
caption = NULL,
x = NULL,
y = NULL,
fill = NULL) +
xlab(NULL)+
ylab(NULL)+
theme_lab()+
theme(panel.grid.major.x = element_blank(), legend.position = "right")
## Warning in if (color == "cluster") color <- "default": la condición tiene
## longitud > 1 y sólo el primer elemento será usado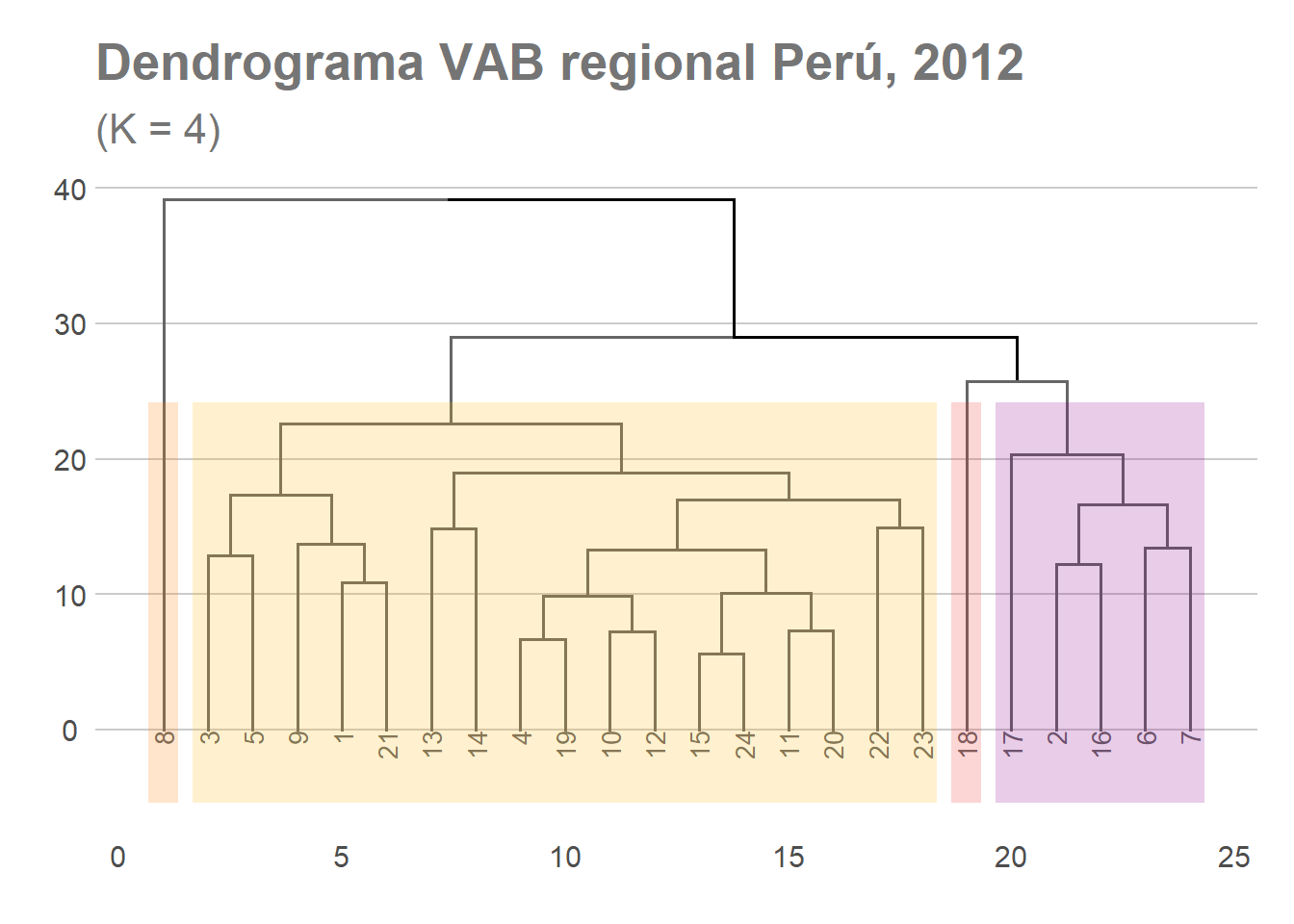
Además de las arriba expuestas, con el paquete fviz_dend() existen otras opciones que pueden resultarnos de interés a la hora de realizar dendrogramas. Veamos algunos ejemplos:
Opción 1.
fviz_dend(DNDvab01,
k = 6,
cex = 0.5,
k_colors = "Set2",
color_labels_by_k = TRUE,
ggtheme = theme_lab())
Opción 2.
fviz_dend(DNDvab01,
cex = 0.7,
k = 6,
k_colors = "jco")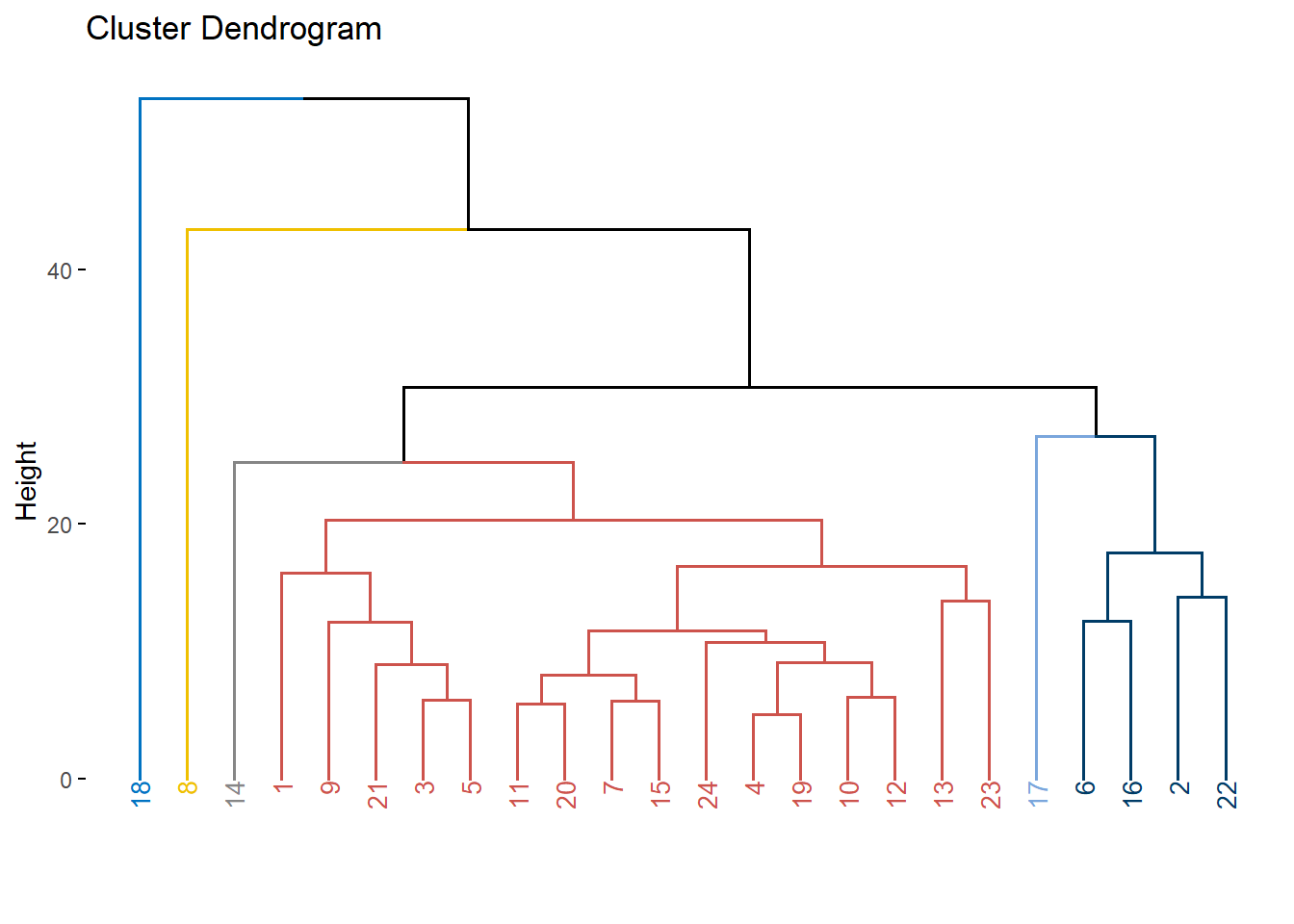
Opción 3.
fviz_dend(DNDvab01,
k = 6,
cex = 0.7,
horiz = TRUE,
k_colors = "jco",
rect = TRUE,
rect_border = "jco",
rect_fill = TRUE)
Opción 4.
fviz_dend(DNDvab01,
cex = 0.8,
k = 6,
k_colors = "jco",
type = "circular")
Opción 5.
fviz_dend(DNDvab01,
k = 6,
k_colors = "jco",
type = "phylogenic",
repel = TRUE)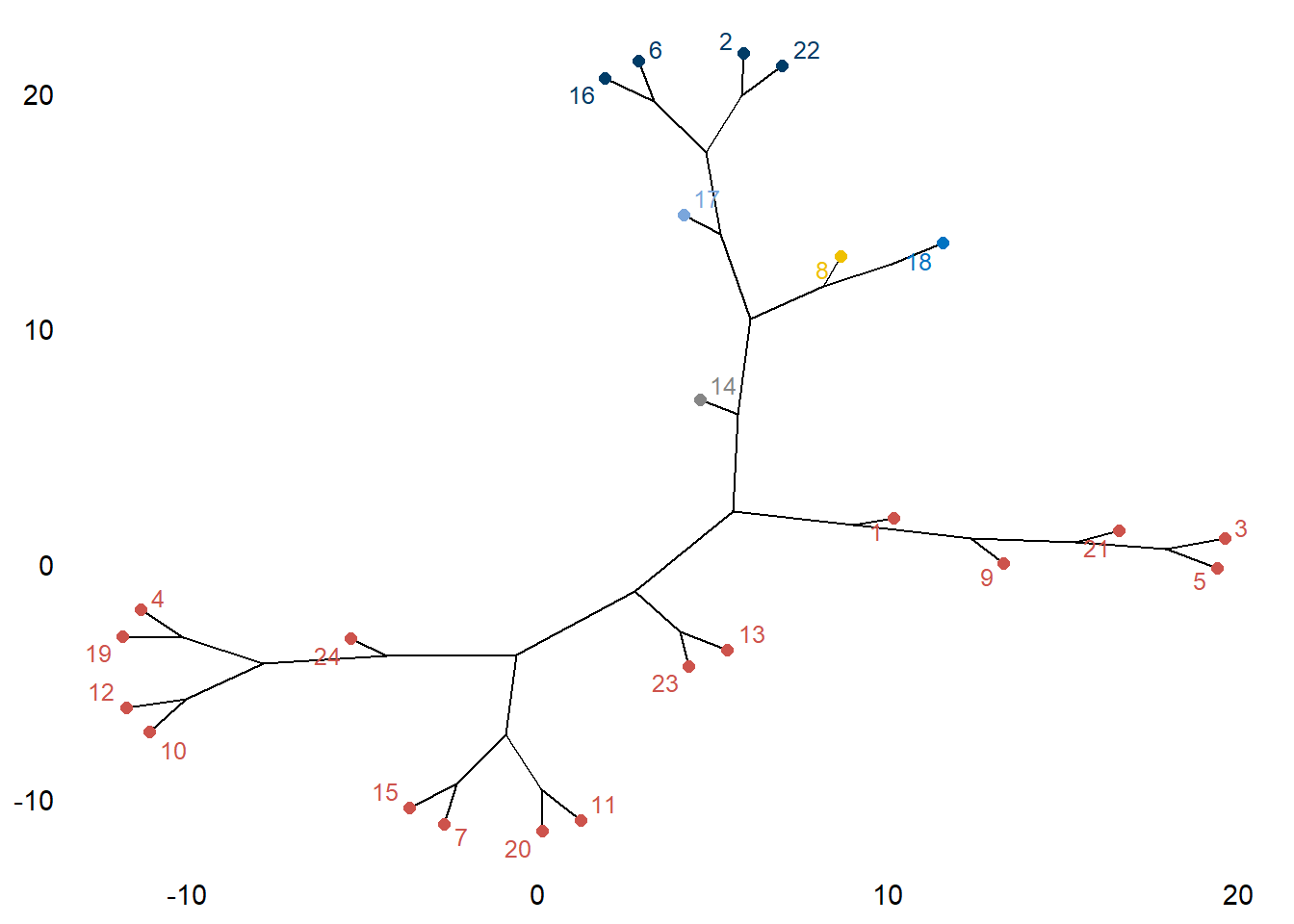
Tablas con información de los conglomerados
Además de representar las agrupaciones de los conglomerados en dendrogramas, resulta de notable interés obtener las características particulares de cada uno de los conglomerados identificados. Presentar esa información en una tabla resulta sencillo siguiendo los pasos realizados a lo largo de este post.
2001
En primer lugar, como vimos, obtenemos la distancia euclídea, tal y como expusimos al inicio del post. Recordemos que la distancia euclídea es la que viene determinada por defecto al usar la función dist(). En primer lugar estimamos las distancias para el año 2001.
dvab01<-dist(ddendvab01)
En segundo lugar realizamos las agrupaciones de los conglomerados siguiendo el criterio de la distancia promedio (average), aunque podríamos haber escogido otro criterio de agrupación, tal y como vimos previamente.
fit.averagevab01<- hclust(dvab01, method="average")
Supongamos que queremos agrupar las regiones peruanas en 6 conglomerados o clusters. En este sentido vemos que el resultado obtenido agrupa en un primer grupo 16 regiones del país (que se corresponde al dendrograma realizado anteriormente), un segundo conglomerado se conforma de 4 regiones y cuatro conglomerados muestran características diferenciadas que se configuran como únicos elementos de sus respectivos conglomerados.
clusters_vab01_ave<- cutree(fit.averagevab01, k=6)
table(clusters_vab01_ave)
## clusters_vab01_ave
## 1 2 3 4 5 6
## 16 4 1 1 1 1
Por último, para ver en una tabla qué características promedio (average) presentan cada uno de los conglomerados, atendiendo a los respectivos sectores productivos, podemos indicar la siguiente orden. En la tabla resultante se observa nítidamente que el gran peso de alguna actividad productiva (Minería en Pasco u Otros Servicios en Huancavelica por ejemplo) explica que algunas regiones configuren un propio conglomerado.
tabla_vab01 <- aggregate(as.data.frame(ddendvab01), by=list(cluster=clusters_vab01_ave), median)
tabla_vab01
## cluster agrvab01 minvab01 manvab01 convab01 comvab01 tycvab01 ryhvab01
## 1 1 18.766445 5.364279 12.686731 5.138297 15.349224 8.095979 3.830943
## 2 2 11.547166 29.434078 9.647819 4.594413 10.153483 6.944116 2.899475
## 3 3 16.959685 7.979819 3.040180 1.041264 5.973317 1.458224 1.099505
## 4 4 4.106135 1.187870 17.889427 5.358595 17.912026 9.718131 5.385479
## 5 5 8.687624 24.435621 33.538543 3.594327 5.463634 3.090353 1.084357
## 6 6 10.946828 57.624432 2.606171 4.447345 6.987572 2.310937 1.175887
## sguvab01 otrvab01
## 1 8.497590 17.996137
## 2 6.458804 16.854246
## 3 7.723001 54.725006
## 4 6.771478 31.670859
## 5 3.529563 16.575977
## 6 4.957223 8.943607
2012
Para el año 2012 el procedimiento sería similar, y únicamente debemos modificar la información referente al año en cuestión.
dvab12<-dist(ddendvab12)
fit.averagevab12<- hclust(dvab12, method="average")
clusters_vab12_ave<- cutree(fit.averagevab12, k=6)
table(clusters_vab12_ave)
## clusters_vab12_ave
## 1 2 3 4 5 6
## 5 4 12 1 1 1
Durante el periodo 2001-2012 parece haberse producido cierto proceso de homogeneización de las estructuras productivas sectoriales de las regiones peruanas. No obstante, tres regiones (Huancavelica, Pasco y Moquegua) registran todavía ciertas características singulares que hace que cada una de dichas regiones configuren, por si solas, un conglomerado. En 2012, por consiguiente, sigue habiendo una notable concentración productiva en algunas de las regiones que componen el país.
tabla_vab12 <- aggregate(as.data.frame(ddendvab12), by=list(cluster=clusters_vab12_ave), median)
tabla_vab12
## cluster agrvab12 minvab12 manvab12 convab12 comvab12 tycvab12 ryhvab12
## 1 1 24.039228 0.5422025 8.412862 13.280094 12.728979 6.004397 4.199933
## 2 2 9.832173 23.1041226 9.619124 7.979920 11.027871 7.006100 4.619254
## 3 3 13.285487 5.2918758 12.140457 8.705849 16.115912 9.994401 3.661230
## 4 4 14.014498 8.0671135 3.023851 2.136559 7.355028 2.000039 1.472483
## 5 5 6.370037 18.9604103 21.225697 18.904682 6.203693 3.821470 1.339633
## 6 6 9.240013 44.2215013 3.585953 6.727540 8.739006 3.159506 1.664869
## sguvab12 otrvab12
## 1 13.421023 12.20891
## 2 8.285583 15.85636
## 3 6.625088 18.97540
## 4 12.567019 49.36341
## 5 5.717623 17.45675
## 6 7.097872 15.56374