Noción de cambio estructural

El concepto de cambio estructural ha sido tradicionalmente un elemento frecuentemente aludido en economía, especialmente en economía del desarrollo. No obstante dicho concepto suele tratarse en la literatura de forma ambigua en tanto en cuanto suele hacer referencia a aspectos muy dispares y a transformaciones de naturaleza diversa y/o multidimensional que registran las sociedades a lo largo de sus procesos de desarrollo. Sin embargo, una de las acepciones más utilizadas en la literatura especializada es la que considera el cambio estructural de una economía como el proceso de transformación de sus estructuras productivas. Esta aproximación es sin duda heredera de las contribuciones de algunos de los llamados pioneros del desarrollo, los cuales defendían que un proceso de desarrollo económico genuino debía caracterizarse por la progresiva transición desde estructuras productivas con gran peso en actividades primarias, principalmente agricultura, hacia otras donde dominase la actividad industrial y actividades de servicios. Por ende, aquellas economías que fuesen capaces de diversificar sus estructuras productivas y reducir el peso de la actividad agrícola, dirigiendo sus recursos hacia otros sectores, serían aquellas que presentarían mayores posibilidades de crecer de forma sostenida y, progresivamente, reducir la pobreza y mejorar la calidad de vida de su población.

No obstante existen voces discordantes entre los expertos acerca de la inevitabilidad de un proceso de esas características en toda experiencia de desarrollo exitosa. De hecho, diversos autores replantean la existencia de configuraciones productivas ganadoras y perdedoras per se, encontrándose en la literatura discrepancias sobre las características específicas que debería presentar un proceso de cambio estructural que pudiera considerare inequívocamente virtuoso y que asegurase asentar las bases de un proceso de desarrollo genuino y sostenible en el tiempo. El papel que juega la actividad industrial sigue siendo motivo de especial interés por parte de muchos economistas como Peneder (2003), Rodrik (2013, 2014, 2016) o Torres y López (2017). Por el contrario, autores como Loayza y Raddatz (2010) o De Janvry y Sadolet (2009) enfatizan el papel de sectores intensivos en trabajo en el proceso de cambio estructural, por ejemplo la agricultura o la construcción, especialmente por impacto sobre el empleo y, con ello, su capacidad de contribuir a la reducción de la pobreza. Por su parte, investigadores como Kapsos (2006) o Fox y Gal (2008) destacan el papel de las actividades de servicios y enfatizan su papel en las economías desarrolladas.

Sea como fuere, la existencia de discrepancias en el papel que juegan los sectores en el proceso de cambio estructural no significa que sus transformaciones a lo largo del tiempo no jueguen un papel fundamental en el desempeño económico de las economía. Dichas transformaciones desempeñarán un papel esencial en el crecimiento económico y, además, a nivel territorial (subnacional) tendrán un impacto significativo sobre la convergencia económica entre las distintas regiones. De hecho, la convergencia territorial en los niveles de productividad y de renta per cápita estará estrechamente relacionada con los cambios en las configuraciones sectoriales del producto pero también con los procesos de movilidad intersectorial de trabajadores. En este sentido autores como McMillan et al (2014) aseguran que un proceso de movilidad intersectorial del empleo que fuese favorable al crecimiento económico (growth enhancing) sería aquel en el que la dirección de dicho traspaso estuviera positivamente correlacionada con la productividad promedio de los sectores individualizados. Por el contrario, un proceso de traspaso de trabajadores que fuese perjudicial para el crecimiento del producto per cápita sería aquel en el que dicha correlación fuese negativa (growth reducing), donde el empleo estaría movilizándose hacia sectores de menor productividad promedio. En esta línea ciertas voces aseguran que la creciente terciarización de las economías desarrolladas, y también de gran parte de economías emergentes, y las dinámicas de desindustrialización serían reflejo de dinámicas de cambio estructural growth reducing que tendrían lugar en las últimas décadas .

El objetivo de este post es modesto y no pretende rebatir o cuestionar ninguno de los planteamientos teóricos presentes en la literatura sobre las características idóneas que debería presentar un proceso de cambio estructural. Simplemente, en el contexto planteado en los párrafos previos y con el pretexto de examinar los procesos de transformación de la estructura sectorial del empleo en las distintas Comunidades Autónomas Españolas en los últimos años, buscando con ello investigar la posible existencia de procesos de cambio estructural growth enhancing o growth reducing, en este post se pretende principalmente mostrar cómo podríamos aproximarnos al análisis de dichas dinámicas utilizando algunas funciones de R y exponer una posible forma de visualizar la evolución de dichos procesos de transformación estructural del empleo a lo largo del tiempo.

Base de datos BDMORES

Para llevar a cabo nuestro objetivo utilizaremos, a precios corrientes, información obtenida de la base de datos BDMORES (Base de datos regionales de España actualizada en junio de 2017) que incluye magnitudes económicas doblemente clasificadas por región y rama de actividad desde 1980 hasta 2011. Previamente se ha seleccionado la información relativa al valor añadido bruto a precios constantes de 2008 (en miles de euros) y de la población ocupada (miles de personas).

En primer lugar, para cargar los datasets seleccionados (formato .xlsx) almacenados en nuestro ordenador cargamos el paquete {readxl}. Por un lado tenemos un data frame con los valores del valor agregado bruto por CCAA y rama de actividad y por otro lado otro dataframe con información de la población ocupada. Podemos ver las primeras líneas de cada dataset utilizando la función head().

library(readxl)

ce_vab <- read_excel("datasets/cambioestructural.xlsx", 
    sheet = "vab")

head(ce_vab)
## # A tibble: 6 x 38
##   Region CCAA  Sector Nombre Actividad Ramas `1980` `1981` `1982` `1983` `1984`
##   <chr>  <chr> <chr>  <chr>  <chr>     <chr>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
## 1 AND    Anda~ Agric~ AGR    Agro      Agri~ 2.78e6 2.67e6 2.51e6 2.51e6 2.83e6
## 2 ARA    Arag~ Agric~ AGR    Agro      Agri~ 9.41e5 5.58e5 6.58e5 7.03e5 9.41e5
## 3 AST    Astu~ Agric~ AGR    Agro      Agri~ 3.97e5 4.08e5 4.15e5 4.13e5 3.92e5
## 4 BAL    Bale~ Agric~ AGR    Agro      Agri~ 2.20e5 1.85e5 1.75e5 1.83e5 1.80e5
## 5 CAN    Cana~ Agric~ AGR    Agro      Agri~ 6.47e5 6.69e5 5.94e5 5.99e5 6.56e5
## 6 CANT   Cant~ Agric~ AGR    Agro      Agri~ 2.68e5 2.86e5 2.60e5 2.76e5 2.79e5
## # ... with 27 more variables: `1985` <dbl>, `1986` <dbl>, `1987` <dbl>,
## #   `1988` <dbl>, `1989` <dbl>, `1990` <dbl>, `1991` <dbl>, `1992` <dbl>,
## #   `1993` <dbl>, `1994` <dbl>, `1995` <dbl>, `1996` <dbl>, `1997` <dbl>,
## #   `1998` <dbl>, `1999` <dbl>, `2000` <dbl>, `2001` <dbl>, `2002` <dbl>,
## #   `2003` <dbl>, `2004` <dbl>, `2005` <dbl>, `2006` <dbl>, `2007` <dbl>,
## #   `2008` <dbl>, `2009` <dbl>, `2010` <dbl>, `2011` <dbl>


ce_peao <- read_excel("datasets/cambioestructural.xlsx", 
    sheet = "peao")

head(ce_peao)
## # A tibble: 6 x 38
##   Region CCAA  Sector Nombre Actividad Ramas `1980` `1981` `1982` `1983` `1984`
##   <chr>  <chr> <chr>  <chr>  <chr>     <chr>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
## 1 AND    Anda~ Agric~ AGR    Agro      Agri~  347.   318.   305.   292.   255  
## 2 ARA    Arag~ Agric~ AGR    Agro      Agri~   87.7   84.1   83.7   80.6   77.9
## 3 AST    Astu~ Agric~ AGR    Agro      Agri~  103.    92.2   74.9   75.2   78.3
## 4 BAL    Bale~ Agric~ AGR    Agro      Agri~   24.7   21.4   20.3   21.5   21  
## 5 CAN    Cana~ Agric~ AGR    Agro      Agri~   86.9   81.1   83.9   79.9   79.1
## 6 CANT   Cant~ Agric~ AGR    Agro      Agri~   40.2   38.4   34.8   34.8   32.8
## # ... with 27 more variables: `1985` <dbl>, `1986` <dbl>, `1987` <dbl>,
## #   `1988` <dbl>, `1989` <dbl>, `1990` <dbl>, `1991` <dbl>, `1992` <dbl>,
## #   `1993` <dbl>, `1994` <dbl>, `1995` <dbl>, `1996` <dbl>, `1997` <dbl>,
## #   `1998` <dbl>, `1999` <dbl>, `2000` <dbl>, `2001` <dbl>, `2002` <dbl>,
## #   `2003` <dbl>, `2004` <dbl>, `2005` <dbl>, `2006` <dbl>, `2007` <dbl>,
## #   `2008` <dbl>, `2009` <dbl>, `2010` <dbl>, `2011` <dbl>

Vemos que ambos datasets tienen un formato largo, es decir, en cada columna a partir de la columna 7 se muestra un año que va desde 1980 hasta 2011. Para trabajar de una forma sencilla estos dataframes conviene recopilar la información en dos columnas, una que indique el año y otra que indique el valor de la variable de interés (vab o población ocupada) por cada observación. Para ello podemos utilizar la función gather() del paquete {tidyverse}. Además, seleccionaremos las columnas que nos interese conservar con la función select().

library(tidyverse)


# para el valor agregado bruto (ce_vab)

ce_vab_gather <- ce_vab %>%
  gather(key= "year", value="vab", 7:38) %>%
  select(Region, CCAA, Nombre, Actividad, Ramas, year, vab)

head(ce_vab_gather)
## # A tibble: 6 x 7
##   Region CCAA     Nombre Actividad Ramas                            year     vab
##   <chr>  <chr>    <chr>  <chr>     <chr>                            <chr>  <dbl>
## 1 AND    Andaluc~ AGR    Agro      Agricultura, ganadería, silvicu~ 1980  2.78e6
## 2 ARA    Aragón   AGR    Agro      Agricultura, ganadería, silvicu~ 1980  9.41e5
## 3 AST    Asturias AGR    Agro      Agricultura, ganadería, silvicu~ 1980  3.97e5
## 4 BAL    Baleares AGR    Agro      Agricultura, ganadería, silvicu~ 1980  2.20e5
## 5 CAN    Canarias AGR    Agro      Agricultura, ganadería, silvicu~ 1980  6.47e5
## 6 CANT   Cantabr~ AGR    Agro      Agricultura, ganadería, silvicu~ 1980  2.68e5


# para la población ocupada (ce_peao)

ce_peao_gather <- ce_peao %>%
  gather(key= "year", value="peao", 7:38) %>%
  select(Region, CCAA, Nombre, Actividad, Ramas, year, peao)

head(ce_peao_gather)
## # A tibble: 6 x 7
##   Region CCAA     Nombre Actividad Ramas                             year   peao
##   <chr>  <chr>    <chr>  <chr>     <chr>                             <chr> <dbl>
## 1 AND    Andaluc~ AGR    Agro      Agricultura, ganadería, silvicul~ 1980  347. 
## 2 ARA    Aragón   AGR    Agro      Agricultura, ganadería, silvicul~ 1980   87.7
## 3 AST    Asturias AGR    Agro      Agricultura, ganadería, silvicul~ 1980  103. 
## 4 BAL    Baleares AGR    Agro      Agricultura, ganadería, silvicul~ 1980   24.7
## 5 CAN    Canarias AGR    Agro      Agricultura, ganadería, silvicul~ 1980   86.9
## 6 CANT   Cantabr~ AGR    Agro      Agricultura, ganadería, silvicul~ 1980   40.2

Una vez hemos dado un formato adecuado a los dos dataframes nos interesa unirlos en un solo dataset, conservando una columna con el valor del vab y otra con la población ocupada para cada una de las observaciones expuestas. Existen diversas formas para unir datasets (profundizaré en este aspecto en un futuro post), pero en esta ocasión utilizaremos la función cbind() conservando las columnas comunes para ambos data frames. Una vez unidos ambos datasets crearemos una nueva columna con la función mutate() para establecer la productividad aparente del trabajo, resultado de dividir el valor agregado bruto entre la población ocupada, columna que llamaremos product.

cambio_estr <- cbind(ce_vab_gather, ce_peao_gather[,7])

cambio_estructural <- cambio_estr %>%
  mutate(product = vab/peao) 

# vemos las primeras columnas del nuevo dataset

head(cambio_estructural)
##   Region      CCAA Nombre Actividad
## 1    AND Andalucía    AGR      Agro
## 2    ARA    Aragón    AGR      Agro
## 3    AST  Asturias    AGR      Agro
## 4    BAL  Baleares    AGR      Agro
## 5    CAN  Canarias    AGR      Agro
## 6   CANT Cantabria    AGR      Agro
##                                          Ramas year     vab  peao   product
## 1 Agricultura, ganadería, silvicultura y pesca 1980 2776590 347.4  7992.487
## 2 Agricultura, ganadería, silvicultura y pesca 1980  941490  87.7 10735.348
## 3 Agricultura, ganadería, silvicultura y pesca 1980  397052 102.9  3858.620
## 4 Agricultura, ganadería, silvicultura y pesca 1980  220089  24.7  8910.486
## 5 Agricultura, ganadería, silvicultura y pesca 1980  646876  86.9  7443.913
## 6 Agricultura, ganadería, silvicultura y pesca 1980  268312  40.2  6674.428

Conviene conocer bien los datos sobre los que trabajamos. Por ello nos interesa examinar con un poco más de profundidad las variables y las observaciones que recoge el dataset sobre el que vamos a trabajar. La función unique() resulta de gran utilidad al examinar las observaciones de los datasets.

unique(cambio_estructural$CCAA)
##  [1] "Andalucía"          "Aragón"             "Asturias"          
##  [4] "Baleares"           "Canarias"           "Cantabria"         
##  [7] "Castilla y León"    "Castilla la Mancha" "Cataluña"          
## [10] "Valencia"           "Extremadura"        "Galicia"           
## [13] "Madrid"             "Murcia"             "Navarra"           
## [16] "País Vasco"         "Rioja"
unique(cambio_estructural$Region)
##  [1] "AND"  "ARA"  "AST"  "BAL"  "CAN"  "CANT" "CYL"  "CLM"  "CAT"  "VAL" 
## [11] "EXT"  "GAL"  "MAD"  "MUR"  "NAV"  "PV"   "RIO"

# La base de datos incluye información sobre 17 CCAA y, por tanto, no incluye las ciudades autónomas de Ceuta y Melilla. CCAA y Region muestran información similar.

unique(cambio_estructural$Actividad)
## [1] "Agro"         "Industria"    "Construcción" "Servicios"
unique(cambio_estructural$Ramas)
##  [1] "Agricultura, ganadería, silvicultura y pesca"                                                                                                          
##  [2] "Industria de la alimentación, fabricación de bebidas e industria del tabaco"                                                                           
##  [3] "Industria textil, confección de prendas de vestir e industria del cuero y del calzado"                                                                 
##  [4] "Industria de la madera y del corcho, industria del papel y artes gráficas"                                                                             
##  [5] "Coquerías y refino de petróleo; industria química; fabricación de productos farmacéuticos"                                                             
##  [6] "Fabricación de productos de caucho y plásticos y de otros productos minerales no metálicos"                                                            
##  [7] "Fabricación de productos informáticos, electrónicos y ópticos; fabricación de material y equipo eléctrico; fabricación de maquinaria y equipo n.c.o.p."
##  [8] "Fabricación de material de transporte"                                                                                                                 
##  [9] "Fabricación de muebles; otras industrias manufactureras y reparación e instalación de maquinaria y equipo"                                             
## [10] "Resto industria"                                                                                                                                       
## [11] "Construcción"                                                                                                                                          
## [12] "Comercio y hostelería"                                                                                                                                 
## [13] "Transporte y comunicaciones"                                                                                                                           
## [14] "Intermediación financiera"                                                                                                                             
## [15] "Otros servicios"
unique(cambio_estructural$Nombre)
##  [1] "AGR"       "IND_ALIM"  "IND_TEXT"  "IND_MAD"   "IND_COQ"   "IND_PLAS" 
##  [7] "IND_INF"   "IND_TRANS" "IND_MUE"   "IND_REST"  "CON"       "COM"      
## [13] "TYC"       "IN_FIN"    "OS"

# La variable Actividad incluye los grandes sectores de la actividad económica: Agricultura, Industria, Construcción y Servicios. La variable Rama incluye 15 subramas de la actividad económica (y la variable Nombre sus abreviaturas). Nótese que en "Resto industria" se incluye también la "Metalurgia y fabricación de productos metálicos, excepto maquinaria y equipo" y en "Otros Servicios" se incluye también el "Alquiler de inmuebles residenciales".

unique(cambio_estructural$year)
##  [1] "1980" "1981" "1982" "1983" "1984" "1985" "1986" "1987" "1988" "1989"
## [11] "1990" "1991" "1992" "1993" "1994" "1995" "1996" "1997" "1998" "1999"
## [21] "2000" "2001" "2002" "2003" "2004" "2005" "2006" "2007" "2008" "2009"
## [31] "2010" "2011"

# El dataset recoge información para el periodo 1980:2011 como indicamos previamente

Estructura sectorial del empleo según productividad promedio de las CCAA en 1980

En primer lugar vamos a ver cómo era la estructura ocupacional del empleo en 1980 por Comunidad Autónoma según la productividad promedio de cada sector productivo. El objetivo que perseguimos es realizar un gráfico donde podamos establecer para cada una de las CCAA la relación entre la productividad relativa de cada una de las 15 ramas de la economía que incluye el dataset y la participación del empleo que cada una de dichas ramas representa sobre la población ocupada total de cada una de las regiones en 1980. Para ello realizaremos una serie de modificaciones sobre el dataset original cambio_estructural.

ce_1980 <- cambio_estructural %>%
  filter(year == 1980) %>%   
  group_by(Region) %>%       
  arrange(Region) %>%        
  mutate( suma_vab = sum(vab)) %>%      
  mutate( suma_peao = sum(peao)) %>%    
  mutate( prod_ccaa = suma_vab / suma_peao ) %>% 
  mutate( prod_relat = log(product/ prod_ccaa)) %>% 
  mutate( peao_relat = 100*(peao / suma_peao)) %>% 
  select(Region, CCAA, Nombre, Actividad, vab, prod_relat, peao_relat)
  
# Las operaciones realizadas son:
# 1. Identificamos el dataset original.
# 2. Filtramos el dataset seleccionando el año 1980.
# 3. Agrupamos el dataset por CCAA.
# 4. Ordenamos el dataset por CCAA (alfabéticamente).
# 5. Creamos una columna (suma_vab) que sume el VAB total por CCAA. 
# 6. Creamos una columna (suma_peao) que sume el peao total por CCAA.
# 7. Creamos una columna (prod_ccaa) que indique la productividad de cada CCAA. 
# 8. Creamos una columna (prod_relat) que muestre la productividad relativa de cada rama con respecto a la productividad total de cada CCAA (en logaritmos).
# 9. Creamos una columna (peao_relat) que indique la participación sectorial del empleo de cada rama con respecto al total del empleo de cada CCAA (%).
# 10. Seleccionamos las columnas que nos interesan.


head(ce_1980)
## # A tibble: 6 x 7
## # Groups:   Region [1]
##   Region CCAA      Nombre   Actividad     vab prod_relat peao_relat
##   <chr>  <chr>     <chr>    <chr>       <dbl>      <dbl>      <dbl>
## 1 AND    Andalucía AGR      Agro      2776590    -1.42       19.2  
## 2 AND    Andalucía IND_ALIM Industria 2418657    -0.130       4.61 
## 3 AND    Andalucía IND_TEXT Industria  591322    -0.701       2.00 
## 4 AND    Andalucía IND_MAD  Industria  561817    -0.0674      1.01 
## 5 AND    Andalucía IND_COQ  Industria 1172748     1.10        0.653
## 6 AND    Andalucía IND_PLAS Industria 1526154     0.456       1.62

Para diferenciar gráficamente las distintas CCAA utilizaremos la función facet_wrap(). Por su parte identificaremos cuatro colores distintos según la actividad económica. En color verde se señalará el sector agricultura, en marrón la industria, en color gris la construcción y en naranja el sector servicios. El eje de abscisas representará la participación sectorial del empleo de cada una de las ramas mientras que el eje de ordenadas indica la productividad relativa de cada rama con respecto a la productividad total de la economía. Por consiguiente, aquellos subsectores que se sitúen por encima de la línea negra horizontal serán sectores que tienen una productividad promedio superior al de la economía en su conjunto y aquellos por debajo serán sectores de menor productividad promedio en el año analizado. Por su parte, el tamaño de cada una de las burbujas representará el VAB de dicho sector en miles de euros, mostrando con ello la importancia de cada uno de estos sectores sobre el VAB total de las CCAA y de la economía nacional en su conjunto.

library(ggrepel)
source("https://github.com/traffordDataLab/assets/raw/master/theme/ggplot2/theme_lab.R")


ce_1980 %>%
  ggplot(aes(x = peao_relat, y = prod_relat)) +
  geom_point(aes(fill= Actividad, 
                 size = vab/1000), 
             shape= 21, 
             colour= "white", 
             alpha= 0.8) +
  facet_wrap(~ CCAA, ncol = 2) +
  scale_size_continuous(range= c(1,25)) +
  scale_fill_manual(values = c("green", "grey40","brown","#FF7A14")) +
  geom_text_repel(aes(label= Nombre, size= 15)) +
  theme_lab() +
  theme(panel.grid.major.x = element_blank(), 
        legend.position = "up", 
        legend.title = element_blank(),
        plot.title = element_text(size = 18, hjust = 0.5),
        plot.subtitle = element_text(size = 14, hjust = 0.5),
        axis.text.x = element_text(size = 8),
        axis.text.y = element_text(size = 8),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10)) +
  geom_hline(yintercept = 0, col= "black", linetype = 1) +
  geom_vline(xintercept = 0, col= "black", linetype = 1) +
  labs(title = "Productividad sectorial relativa\n Vs.\n Participación sectorial del empleo", 
       subtitle = "Por Comunidades Autónomas en 1980", 
       x = "Employment share in 1980",  
       y = "log (sectoral y/ total y)",
       caption = "Fuente: BDMORES")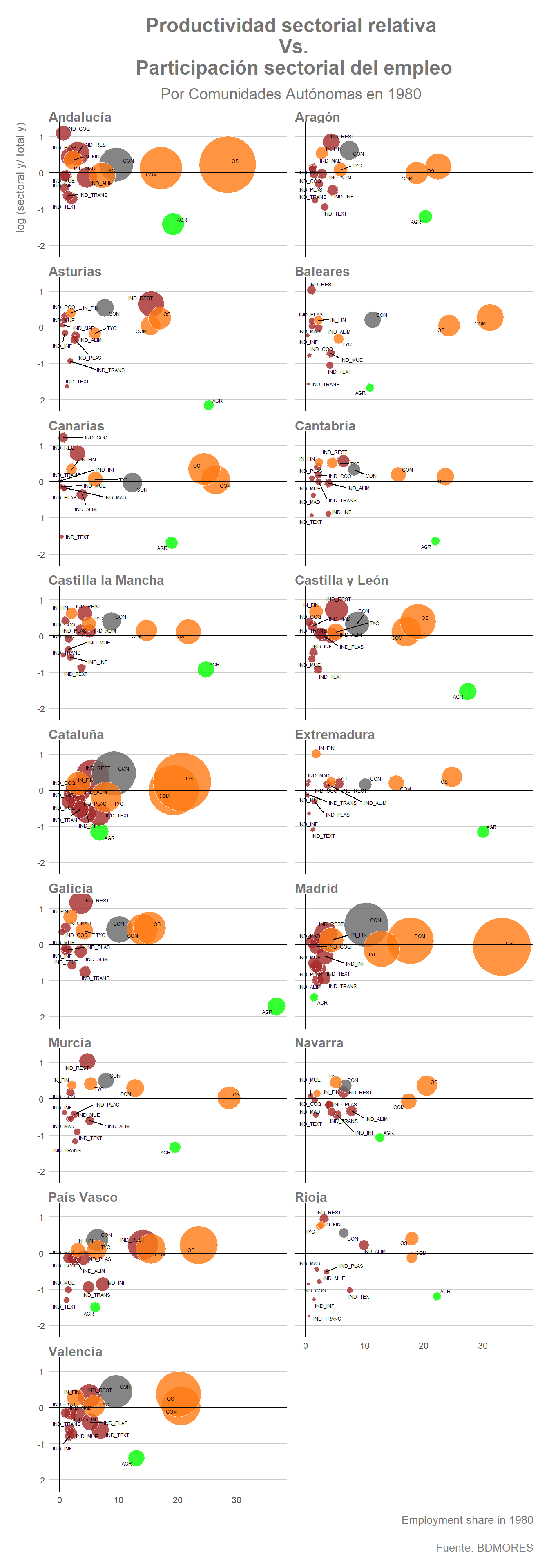

# Una vez tenemos el código para uno de los años podemos fácilmente modificarlo para examinar cualquier otro año del periodo.  

Resulta patente la importancia que ya en 1980 tenía el sector servicios en el empleo, especialmente los sectores “Otros Servicios” y el sector “Comercio” en gran parte de las economías regionales españolas, especialmente en Andalucía, Madrid, País Vasco o Valencia. Además, por lo general, a excepción de Madrid, estos sectores presentaban una productividad promedio superior al promedio de dichas economías. No obstante, las actividades que por lo general presentaban una mayor productividad promedio eran actividades del sector industrial, a pesar de que dichas actividades representaban una menor participación del empleo en todas las CCAA. Por su parte, como cabía esperar, el sector “Agricultura” es el sector que presenta menores niveles de productividad promedio en todas las regiones con respecto al resto de sectores. Además, como se observa en los gráficos, en algunas regiones este sector representaba una participación considerable del empleo total en 1980, especialmente en regiones como Andalucía, Aragón, Asturias, Cantabria, Extremadura, Castilla y León, Galicia o La Rioja. La actividad industrial, por el contrario, registra una menor participación del empleo y su productividad promedio depende en gran medida de la subrama a considerar, habiendo actividades industriales de alta productividad relativa y otras de menor productividad promedio, generalmente la industria textil o del transporte. A grandes rasgos, sin ánimo de ser exhaustivos, se podría decir que en la mayor parte de CCAA autónomas en España en 1980 la estructura ocupacional estaba dominada por actividades de servicios y por la actividad agrícola.

Gráfico animado

Para observar en un único gráfico cómo ha sido la evolución de la productividad relativa de cada rama de la estructura económica con respecto a la productividad de cada región conjuntamente con los cambios en la participación sectorial del empleo en cada uno de estos sectores podemos realizar un gráfico animado utilizando el paquete {gganimate} conjuntamente con {ggplot2}. Para ello modificaremos el dataframe original (cambio_estructural), agrupando las observaciones por año y por Comunidad Autónoma.

todas_ccaa <- cambio_estructural %>%
  group_by(year, CCAA) %>%
  arrange(year, CCAA) %>%
  mutate( suma_vab = sum(vab)) %>%
  mutate( suma_peao = sum(peao)) %>%
  mutate( prod_ccaa = suma_vab / suma_peao ) %>%
  mutate( prod_relat = log(product/ prod_ccaa)) %>%
  mutate( peao_relat = 100*(peao / suma_peao)) %>%
  select(year, CCAA, Nombre, Actividad, vab, prod_relat, peao_relat)


# las 20 primeras filas del nuevo dataset son:

head(todas_ccaa, n = 20)
## # A tibble: 20 x 7
## # Groups:   year, CCAA [2]
##    year  CCAA      Nombre    Actividad         vab prod_relat peao_relat
##    <chr> <chr>     <chr>     <chr>           <dbl>      <dbl>      <dbl>
##  1 1980  Andalucía AGR       Agro          2776590    -1.42       19.2  
##  2 1980  Andalucía IND_ALIM  Industria     2418657    -0.130       4.61 
##  3 1980  Andalucía IND_TEXT  Industria      591322    -0.701       2.00 
##  4 1980  Andalucía IND_MAD   Industria      561817    -0.0674      1.01 
##  5 1980  Andalucía IND_COQ   Industria     1172748     1.10        0.653
##  6 1980  Andalucía IND_PLAS  Industria     1526154     0.456       1.62 
##  7 1980  Andalucía IND_INF   Industria      331774    -0.407       0.835
##  8 1980  Andalucía IND_TRANS Industria      449915    -0.631       1.42 
##  9 1980  Andalucía IND_MUE   Industria      496089    -0.0816      0.902
## 10 1980  Andalucía IND_REST  Industria     3146472     0.546       3.05 
## 11 1980  Andalucía CON       Construcción  7226562     0.236       9.56 
## 12 1980  Andalucía COM       Servicios    11605641     0.124      17.2  
## 13 1980  Andalucía TYC       Servicios     4010545    -0.0665      7.18 
## 14 1980  Andalucía IN_FIN    Servicios     1959274     0.357       2.30 
## 15 1980  Andalucía OS        Servicios    21430188     0.231      28.5  
## 16 1980  Aragón    AGR       Agro           941490    -1.20       20.3  
## 17 1980  Aragón    IND_ALIM  Industria      412068    -0.0306      2.75 
## 18 1980  Aragón    IND_TEXT  Industria      195078    -0.941       3.23 
## 19 1980  Aragón    IND_MAD   Industria      221043     0.155       1.22 
## 20 1980  Aragón    IND_COQ   Industria      208260    -0.0447      1.41

# las 20 últimas filas son:

tail(todas_ccaa, n = 20)
## # A tibble: 20 x 7
## # Groups:   year, CCAA [2]
##    year  CCAA     Nombre    Actividad         vab prod_relat peao_relat
##    <chr> <chr>    <chr>     <chr>           <dbl>      <dbl>      <dbl>
##  1 2011  Rioja    CON       Construcción   724266     0.146       8.41 
##  2 2011  Rioja    COM       Servicios     1195240    -0.210      19.8  
##  3 2011  Rioja    TYC       Servicios      372856     0.245       3.92 
##  4 2011  Rioja    IN_FIN    Servicios      312681     0.941       1.64 
##  5 2011  Rioja    OS        Servicios     2304941    -0.151      36.0  
##  6 2011  Valencia AGR       Agro          1849193    -0.400       2.95 
##  7 2011  Valencia IND_ALIM  Industria     2659836     0.261       2.19 
##  8 2011  Valencia IND_TEXT  Industria     1392188    -0.604       2.73 
##  9 2011  Valencia IND_MAD   Industria     1202060    -0.0264      1.32 
## 10 2011  Valencia IND_COQ   Industria     1431293     0.825       0.671
## 11 2011  Valencia IND_PLAS  Industria     2750229     0.227       2.35 
## 12 2011  Valencia IND_INF   Industria     1016650     0.0392      1.05 
## 13 2011  Valencia IND_TRANS Industria      884296     0.107       0.851
## 14 2011  Valencia IND_MUE   Industria     1150060    -0.136       1.41 
## 15 2011  Valencia IND_REST  Industria     3775421     0.462       2.55 
## 16 2011  Valencia CON       Construcción 11449001     0.432       7.95 
## 17 2011  Valencia COM       Servicios    18804581    -0.248      25.8  
## 18 2011  Valencia TYC       Servicios     6936581     0.213       6.00 
## 19 2011  Valencia IN_FIN    Servicios     4508844     0.841       2.08 
## 20 2011  Valencia OS        Servicios    33594542    -0.109      40.1

Una vez hemos establecido el dataframe podemos realizar un gráfico animado donde se reflejen los cambios en las distintas variables que han tenido lugar entre 1980 y 2011. Para ello utilizaremos la función transition_states() de {gganimate} indicando de esta forma que queremos hacer la transición año por año.

library(gganimate)

todas_ccaa  %>%
  ggplot(aes(x = peao_relat, y = prod_relat)) +
  geom_point(aes(fill= Actividad, 
                 size = vab/1000), 
             shape= 21, 
             colour= "white", 
             alpha= 0.8) +
  scale_size_continuous(range= c(1,30)) +
  scale_fill_manual(values = c("green", "grey40","brown","#FF7A14")) +
  facet_wrap(~ CCAA,ncol= 2) +
  transition_states(year) +
  labs(title = "Productividad sectorial relativa\n VS.\n Participación sectorial del empleo",
       subtitle = "Year: {closest_state}",
       x = "Employment share",  
       y = "log (sectoral y/ total y)",
       caption = "Fuente: BDMORES") +
  shadow_wake(wake_length = 0.05, alpha = T) +
  theme_lab() +
  theme(panel.grid.major.x = element_blank(), 
        legend.position = "up",
        legend.title = element_blank(),
        plot.title = element_text(size = 18, hjust = 0.5),
        plot.subtitle = element_text(size = 16, hjust = 0.5),
        axis.text.x = element_text(size = 8),
        axis.text.y = element_text(size = 8),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10)) +
  geom_hline(yintercept = 0, col= "black", linetype = 1) +
  geom_vline(xintercept = 0, col= "black", linetype = 1)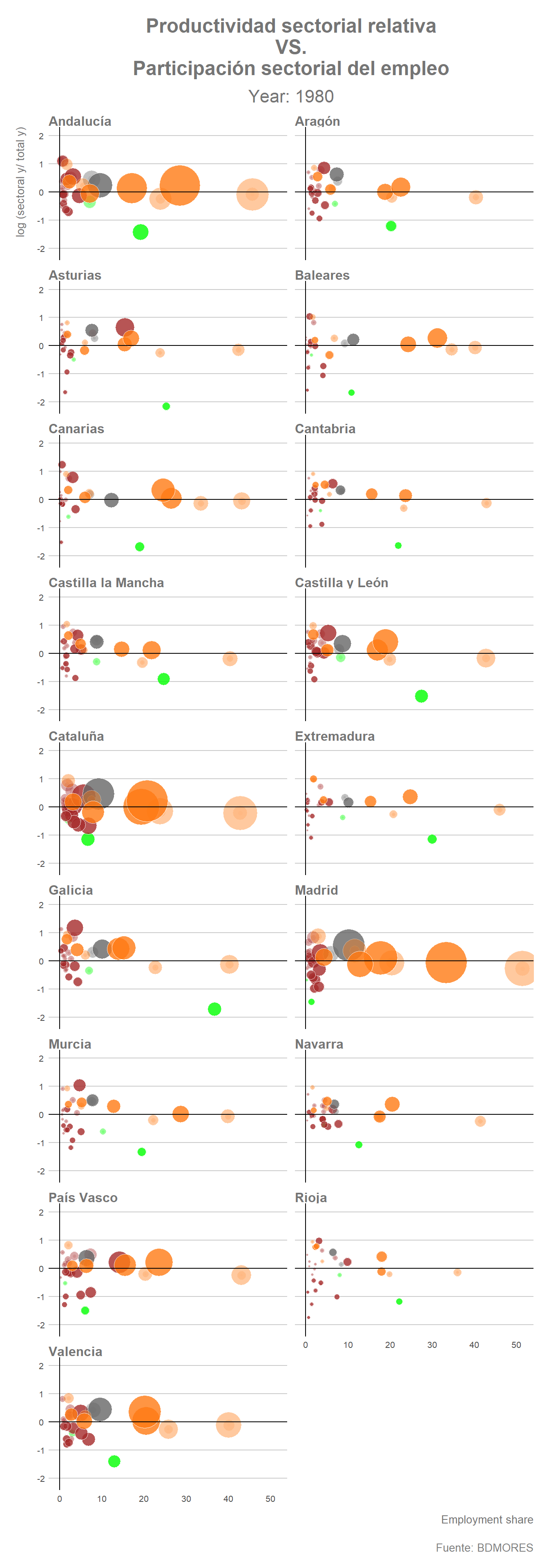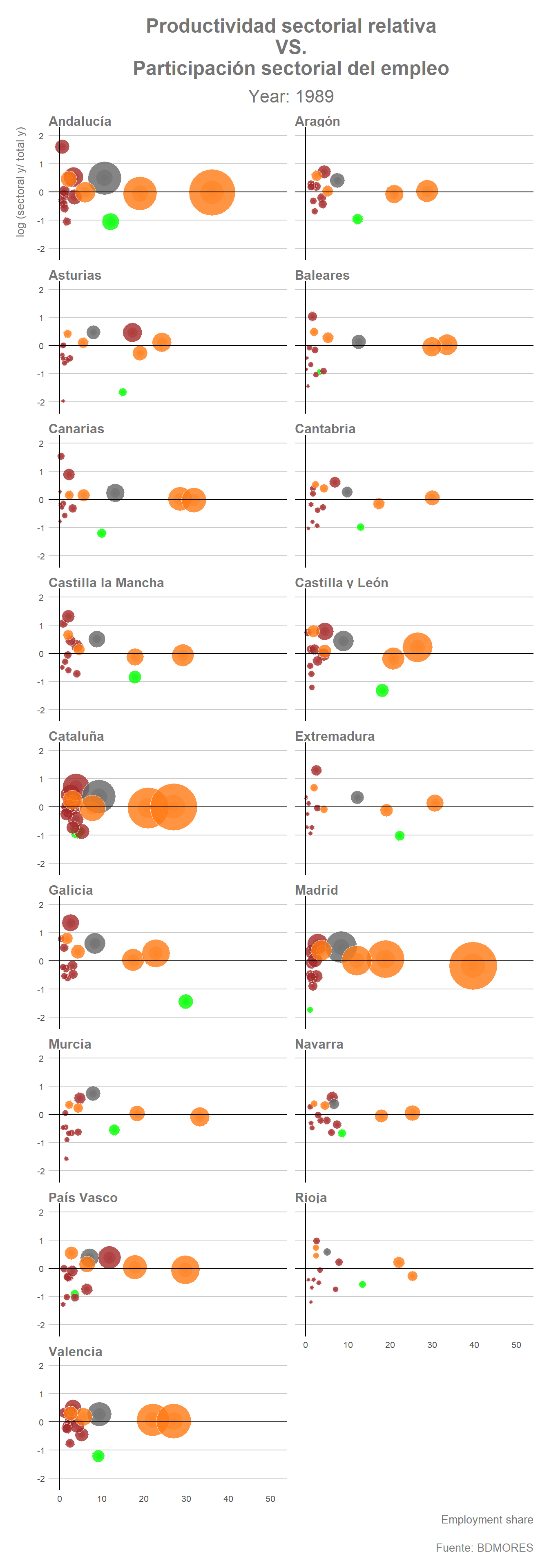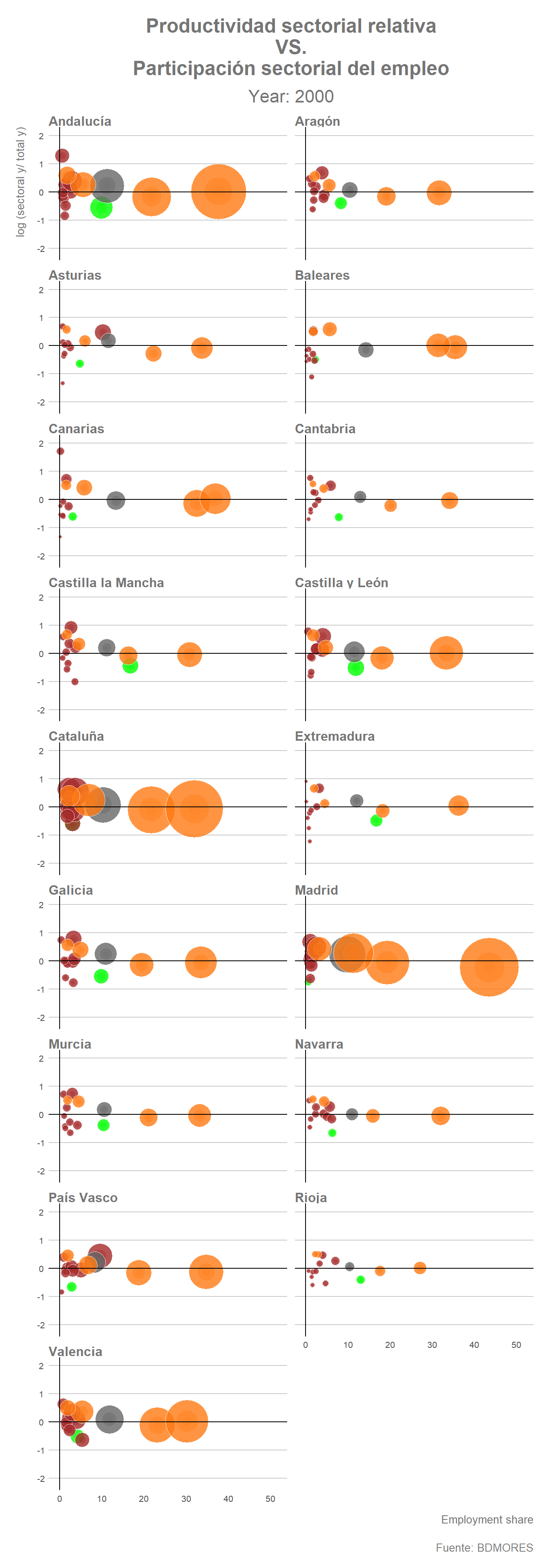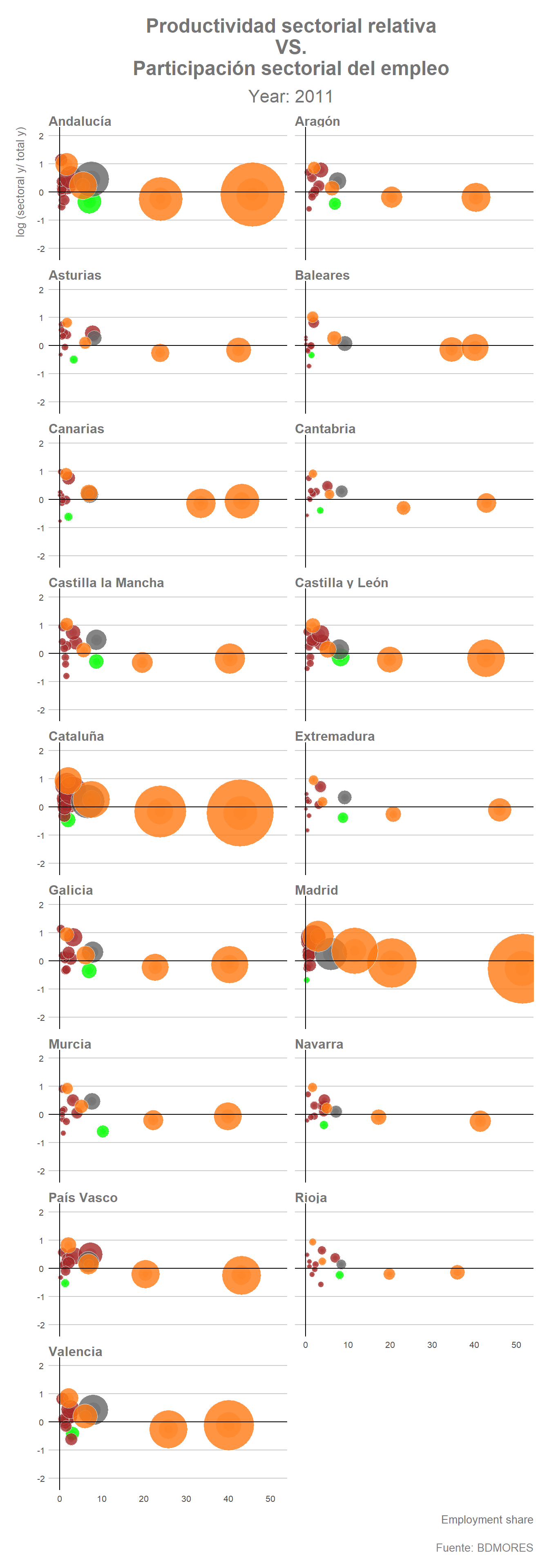 

El gráfico animado muestra claramente que el proceso de terciarización se ha profundizado progresivamente durante el periodo considerado (1980-2011) en prácticamente todas las regiones. Por el contrario, la evolución que refleja el gráfico indica claramente como con el paso de los años la participación del empleo en el sector “Agricultura” también ha tendido a reducirse en gran parte de las regiones españolas, especialmente aquellas que partían de una mayor proporción del empleo agrícola en sus estructuras ocupacionales en el año inicial del periodo. La evolución de la estructura del empleo de las regiones españolas entre 1980 y 2011 parece indicar que durante este periodo se ha profundizado, por tanto, en el proceso de terciarización y de desagrarización del empleo. La actividad industrial, por su parte, parece mantener una posición relativamente estable, con ciertas excepciones como por ejemplo el caso de Asturias donde ha tenido lugar una notable reducción de la participación del empleo industrial (especialmente de la industria metalúrgica) sobre el empleo total de dicha Comunidad Autónoma.

¿Cambio estructural growth enhancing o growth reducing?

Los gráficos realizados previamente nos permiten hacernos una idea de cómo era la estructura sectorial del empleo en 1980 y cómo ha ido evolucionando a lo largo del periodo considerado. No obstante, resulta necesario completar dicho análisis con alguna evidencia que nos permita considerar de una forma más adecuada si los procesos de movilidad laboral observados han sido favorables al crecimiento de las regiones o si, por el contrario, habrían sido perjudiciales para el mismo. Cómo señalamos en el apartado introductorio, según McMillan et al. (2014), un proceso de movilidad intersectorial de trabajadores que fuese favorable al crecimiento sería aquel en la cual dicho traspaso estuviera positivamente relacionada con la productividad relativa de los sectores seleccionados, redireccionándose el empleo hacia sectores de mayor productividad promedio. En dicha ocasión se podría considerar que dicho proceso ha sido growht enhancing. Por el contrario, si dicho proceso estuviera negativamente correlacionado, es decir, si el incremento de la participación del empleo hubiera tenido lugar en sectores de menor productividad promedio, dicha dinámica podría considerarse según estos autores como growth reducing. Gráficamente esta condición se representaría como la relación de la productividad relativa de los distintos sectores de cada economía (eje de abscisas) con respecto al cambio en la participación del empleo en cada uno de ellos (eje de ordenadas).

Para llevar a cabo esta representación gráfica modificaremos los datasets utilizados previamente (ce_vab y ce_peao) aunque de forma ligeramente diferente a como lo hemos hecho para los gráficos previos. Centraremos el análisis en el año inicial y final aunque un análisis en mayor profundidad debería considerar subperiodos de tiempo.

# seleccionamos únicamente los años 1980 y 2011 en ambos datasets (y renombramos las columnas)

ce_vab$vab_1980 <- ce_vab$`1980`
ce_vab$vab_2011 <- ce_vab$`2011`

ce_vab_2 <- ce_vab  %>%
  select(CCAA, Nombre, Actividad, vab_1980, vab_2011)

ce_peao$peao_1980 <- ce_peao$`1980`
ce_peao$peao_2011 <- ce_peao$`2011`

ce_peao_2 <- ce_peao  %>%
  select(CCAA, Nombre, Actividad, peao_1980, peao_2011)


# Unimos ambos datasets en uno: 

cambio_estr_2 <- cbind(ce_vab_2, ce_peao_2[,4:5])

# Las primeras filas del dataset son:

head(cambio_estr_2)
##        CCAA Nombre Actividad vab_1980 vab_2011 peao_1980 peao_2011
## 1 Andalucía    AGR      Agro  2776590  6766581     347.4     208.9
## 2    Aragón    AGR      Agro   941490  1427819      87.7      41.5
## 3  Asturias    AGR      Agro   397052   413867     102.9      13.4
## 4  Baleares    AGR      Agro   220089   225131      24.7       6.3
## 5  Canarias    AGR      Agro   646876   412177      86.9      15.9
## 6 Cantabria    AGR      Agro   268312   269603      40.2       7.9

Una vez unidos los dataframes modificamos el dataset final para obtener para cada región y subsector la productividad relativa de cada sector sobre la economía regional en su conjunto en el año final y el cambio en la participación relativa del empleo entre 1980 y 2011.

ce_1980_2011 <- cambio_estr_2 %>%
  arrange(CCAA) %>%
  mutate(prod_sectorial_1980 = vab_1980/peao_1980, prod_sectorial_2011 = vab_2011/peao_2011) %>%
  group_by(CCAA) %>%
  mutate(suma_vab_1980 = sum(vab_1980), suma_peao_1980 = sum(peao_1980), suma_vab_2011 = sum(vab_2011), suma_peao_2011 = sum(peao_2011)) %>%
  mutate(prod_ccaa_1980 = suma_vab_1980/suma_peao_1980, prod_ccaa_2011 = suma_vab_2011/suma_peao_2011) %>%
  mutate(prod_relat_1980 = log(prod_sectorial_1980/prod_ccaa_1980), prod_relat_2011= log(prod_sectorial_2011/prod_ccaa_2011)) %>%
  mutate(peao_relat_1980 = 100*(peao_1980/suma_peao_1980), peao_relat_2011 = 100*(peao_2011/suma_peao_2011)) %>%
  mutate(cambio_peao = peao_relat_2011 - peao_relat_1980)

Por último graficamos la información estimada en el paso anterior. En esta ocasión el tamaño de las burbujas representa el número de trabajadores en cada sector en el año final del periodo. En base a ello indicamos para cada Comunidad Autónoma la dirección e inclinación de la correlación simple (línea continua) y ponderada por número de población ocupada (línea discontinua). Por tanto, como indicábamos previamente, una relación positiva de la línea de regresión sería indicio de un proceso de cambio estructural growth enhancing y una relación negativa indicaría un proceso de tipo growth reducing.

ce_1980_2011 %>%
  ggplot(aes(x= cambio_peao, y= prod_relat_2011)) +
  geom_point(aes(fill= Actividad, 
                 size = peao_1980/10), 
             shape= 21, colour= "white", 
             alpha= 0.8, 
             stroke= 1.05) +
  geom_smooth(method = "lm", se= FALSE, 
              colour = "black", 
              size = 0.5) +
  geom_smooth(method = "lm", se= FALSE, 
              colour = "black", 
              aes(weight= peao_1980), 
              linetype = 2, 
              size = 0.5) +
  scale_size_continuous(range = c(0,25)) +
  scale_fill_manual(values= c("green", "grey40","brown","#FF7A14")) +
  geom_text_repel(aes(label = Nombre, size = 0.3)) +
  theme_lab() +
  theme(panel.grid.major.x = element_blank(), 
        legend.position = "up", 
        legend.title = element_blank(),
        axis.text.x = element_text(size = 8),
        axis.text.y = element_text(size = 8),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))+
  labs(title = "¿Growth enhancing o growth reducing?", 
       subtitle = "", 
       x = "Change in employment share",  
       y = "log (sectoral y/ total y)",
       caption = "Fuente: BDMORES") +
  geom_hline(yintercept=0, col="darkgrey", linetype=2)+
  geom_vline(xintercept=0, col="darkgrey", linetype=2)+
  facet_wrap(~ CCAA, ncol = 2)
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'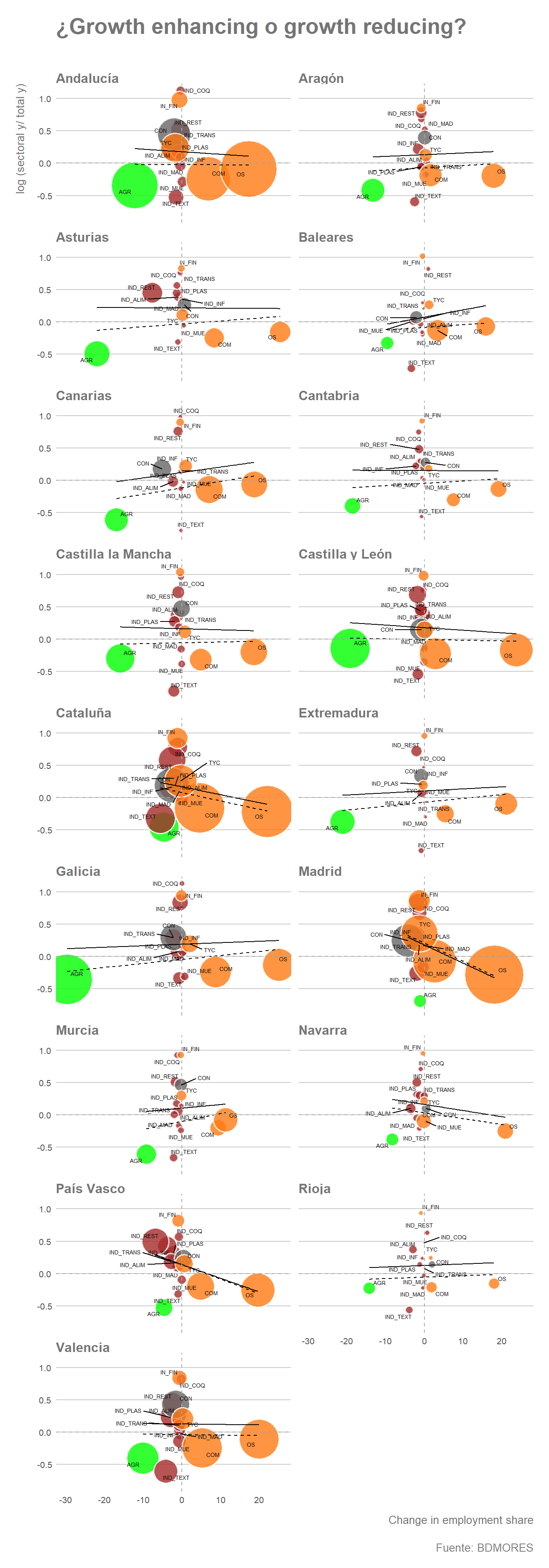

Como se vio en el apartado previo, la actividad comercial y otras actividades de servicios han incrementado su peso relativo de forma notable a lo largo de las últimas décadas en prácticamente todas las regiones del país, a pesar de que los niveles de productividad promedio de estos sectores (al menos al final del periodo) muestran un valor inferior al de la mayoría del resto de sectores. Sin embargo, la dirección de las rectas de regresión, que serían indicativos de la eficacia de los procesos de movilidad intersectorial de trabajadores, presentan características heterogéneas. Por lo general, en Comunidades Autónomas que registran un mayor nivel de renta por habitante con respecto al resto de CCAA, véase Madrid, Cataluña, País Vasco o Navarra, dichos procesos de movilidad laboral serían claramente growth reducing, independientemente de si tenemos en cuenta el tamaño relativo del sector (en número de ocupados) en la regresión o no. Por el contrario, regiones de menor nivel de VAB por habitante, que por lo general han reducido en mayor medida su población ocupada en la actividad agrícola, muestran una dinámica positiva, favorable al crecimiento en dichas regiones, a pesar de sufrir un proceso de desindustrialización similar a la del grupo anterior. Entre estas regiones destacan especialmente Extremadura, Murcia o Galicia. Por consiguiente, resulta patente que, en términos generales, las regiones de menor nivel de renta presentan una correlación favorable debido, fundamentalmente, a la mayor pérdida de peso relativo del empleo agrícola mientras que, por el contrario, las regiones de mayor VAB por habitante, entre ellas la región capitalina, registran movimientos intersectoriaes del empleo desfavorables a su crecimiento, en tanto que se dirigen mayoritariamente del sector manufacturero e industrial a sectores de servicios de menor productividad promedio. La creciente terciarización de las economías más ricas podría por tanto suponer un handicap importante para su crecimiento futuro.

La evolución observada habrá tenido, con toda seguridad, un impacto en las dinámicas de convergencia en renta per cápita de las regiones españolas. No obstante, los datos sugieren que dicho proceso habrá sido lo que algunos autores denominan convergencia depresiva o a la baja, resultado no tanto del buen desempeño de las regiones menos favorecidas sino por el peor comportamiento relativo de las regiones que partían de una posición privilegiada. No obstante, por motivo de espacio, las dinámicas de convergencia territorial entre las Comunidades Autónomas se analizarán en otro post.