Re
En esta serie se llevará a cabo un recorrido por las distribuciones de probabilidad más comunes. En esta primera entrada se profundizará en la distribución Bernoulli y en la distribución Binomial.
Paquetes
library(dplyr)
library(ggplot2)
library(ggthemes)
Introducción
Por lo general, el paquete {stats} de R (base R) que viene instalado por defecto incluye funciones para realizar operaciones asociadas a un gran número de distribuciones de probabilidad. La lista completa de las distribuciones incluidas en el paquete {stats} se obtiene indicando el siguiente comando: help("Distributions"), el cual nos devolverá la captura de pantalla que veremos a continuación. Se comprueba que el paquete {stats} incluye las distribuciones de probabilidad más comunes (binomial, chi-squared, exponential, F-distribution, normal distribution, etc.).
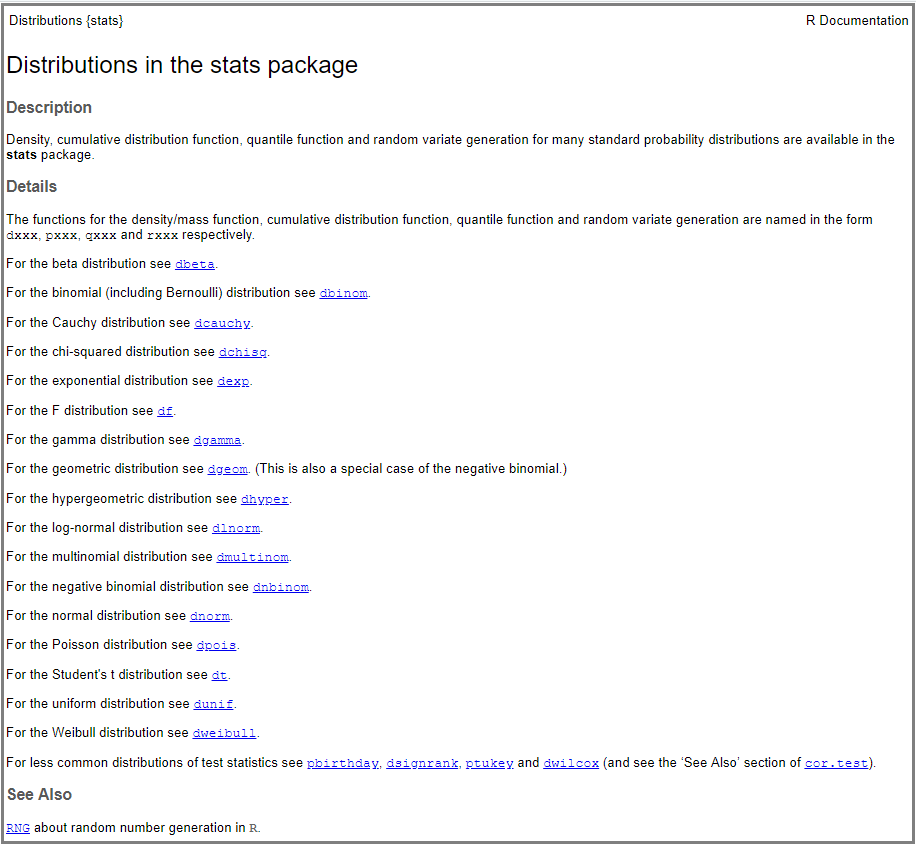
No obstante, téngase en cuenta que en CRAN podemos acceder a un gran número de paquetes donde se incluyen otras distribuciones más especializadas, u otros paquetes alternativos para trabajar con las distribuciones ya incluidas en {stats}. Una lista de dichos paquetes se puede consultar en el siguiente enlace.
En {stats} cada distribución de probabilidad tiene un nombre asignado y para cada una de ellas existen cuatro distintas funciones: función de densidad o de probabilidad (density), función de distribución (distribution function), función cuantílica (quantile function) y una función para la generación de números aleatorios (random variate generation), tal y como se explica en los detalles de la captura de pantalla mostrada previamente. Como se puede deducir de los respectivos nombres, la función density calcula la densidad (pdf) en un determinado valor, la función de distribución nos devuelve la distribución acumulada (cdf), la función cuantílica calcula el cuantil correspondiente a una determinada probabilidad y la última función genera un conjunto de valores aleatorios de una determinada distribución. Dichas funciones se indican anteponiendo los prefijos: d, p, q o r respectivamente al nombre asignado a cada distribución. Por ejemplo, para el caso de la distribución binomial, que trataremos en este post, las funciones serán: dbinom(), pbinom(), qbinom() y rbinom()
Señalar que entre las distribuciones incluidas en {stats} podemos diferenciar entre distribuciones discretas y distribuciones continuas, donde las primeras no asumen valores intermedios entre dos números enteros mientras que las segundas si lo hacen. Entre las primeras distribuciones discretas encontramos, por ejemplo, la distribución binomial (binom), la distribución Poisson (pois) o la geométrica (geom). Entre las continuas tenemos la distribución normal (norm), la t-Student (t) o la distribución chi-cuadrado (chisq) entre otras.
Distribución de Bernoulli
Para explicar la distribución de Bernoulli suele ser habitual utilizar el ejemplo clásico de la moneda. Supongamos que lanzamos una moneda al aire para escoger quién realiza determinada acción y, claro está, el resultado solo podrá ser cara o cruz. El resultado de un único intento, es decir, de una única vez que lanzamos la moneda para observar si la moneda muestra uno u otro resultado, sería un ejemplo clásico de distribución de Bernoulli. Es decir, un único intento con dos posibles resultados. Este ejemplo de lanzamiento de moneda lo podemos representar en R de la siguiente forma:
sample(c("Cara", "Cruz"), 1)
## [1] "Cara"
sample(c("Cara", "Cruz"), 1)
## [1] "Cruz"
sample(c("Cara", "Cruz"), 1)
## [1] "Cara"
En este caso la variable aleatoria toma dos posibles valores cuya probabilidad será p y 1 - p. En el caso de que la moneda no tuviera ningún elemento que favoreciese un resultado sobre el otro la probabilidad de que el resultado fuese cruz sería de 0,5 y la probabilidad de que fuese cara sería 1 - 0,5 = 0,5. Evidentemente, en el caso de que la moneda estuviera trucada y favoreciese un resultado (ej.cara) con respecto a la otra posibilidad la probabilidad de dicho resultado sería superior, pongamos 0,7, mientras que la probabilidad de que saliese cruz sería de 0,3.
Nota: Para saber un poco más sobre quién fue Daniel Bernoulli aquí está el link a su entrada en Wikipedia
Distribución Binomial
Ahora supongamos que repetimos la misma operación. Es decir, realizamos un número determinado de lanzamientos de la moneda para observar si el resultado obtenido un mayor número de veces es cara o cruz. Dicha sucesión de lanzamientos, que en sí ya se podría considerar como experimento, vendría reflejada por lo que se conoce como distribución binomial. Por ende, la distribución de probabilidad binomial describirá el resultado de n operaciones independientes que comparten la misma probabilidad y donde existen dos posibles resultados (cara o cruz, verdadero o falso, éxito o fracaso, etc.), tal y como sucede por ejemplo en el caso del lanzamiento de la moneda. Si partimos de lo expuesto previamente en la distribución de Bernoulli, si la probabilidad de uno de los posibles resultados, digamos cara, es p, entonces la probabilidad de obtener x caras en un experimento de n lanzamientos será:
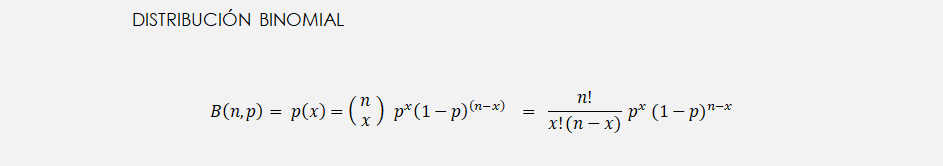
Nota: Para un recordatorio sobre el uso de factoriales puede consultar el siguiente enlace
Veamos algún ejemplo de posibles resultados obtenidos con la función rbinom(). Como se expuso previamente, dicha función nos devuelve un conjunto de valores aleatorios en función de los parámetros indicados. Un ejemplo de 20 posibles resultados obtenidos al lanzar una moneda cada vez (sería también posible obtener el resultado del lanzamiento de dos o más monedas cada vez) con una probabilidad de p = 0.5 de que el resultado sea cara se estima de la siguiente forma:
rbinom(20, 1, 0.5)
## [1] 1 1 1 1 1 1 0 1 0 1 0 1 1 1 1 1 1 1 0 0
Para determinar la probabilidad de obtener un determinado resultado podemos hacer uso de la fórmula presentada previamente. Por tanto, para obtener, por ejemplo, la probabilidad de que el resultado de nuestro experimento sean seis caras en 10 lanzamientos, siendo la probabilidad de p = 0.5, indicaríamos el siguiente código donde sustituimos nuestros valores en la ecuación presentada anteriormente:
n = 10
x = 6
p = 0.5
choose(n,x)*p^x*(1-p)^(n-x)
## [1] 0.2050781
Sin embargo, el paquete {stats} nos facilita llevar a cabo dicha operación con la función dbinom(). Por consiguiente, obtendremos el mismo resultado, basado en las premisas planteadas en el ejercicio anterior, utilizando dbinom() de la siguiente forma:
dbinom(x= 6, size = 10, prob = 0.5)
## [1] 0.2050781
Podemos representar gráficamente las probabilidades para cada uno de los resultados (ver siguiente gráfico). En color naranja observamos que la probabilidad de obtener seis veces cara, en 10 lanzamientos y p = 0.5 sería de 0.205. Dado la probabilidad y el número de lanzamientos escogidos, el resultado más probable de nuestro experimento sería obtener cinco veces cara (y por tanto cinco veces cruz).
data.frame(lanzam = 0:10, p = dbinom(x = 0:10, size = 10, prob = 0.5)) %>%
mutate(result = ifelse(lanzam == 6, "si", "no")) %>%
ggplot(aes(x = factor(lanzam), y = p, fill = result)) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 4,
vjust = 0) +
labs(title = "¿Cuál es la probabilidad de obtener seis veces `cara`?",
subtitle = "(p = 0,5)",
x = "Número de veces donde el resultado es `cara`",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))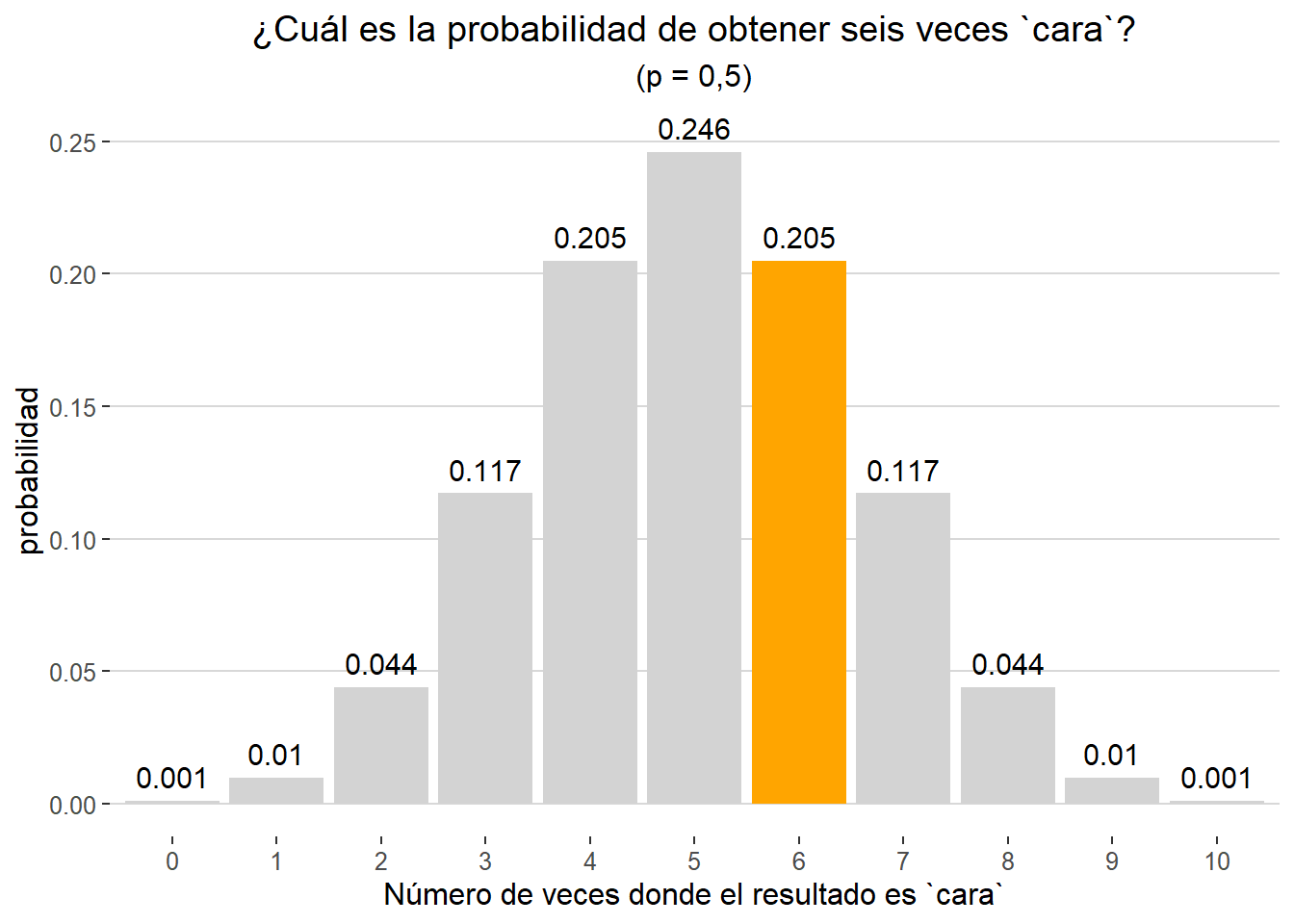
Para obtener cada una de las probabilidades de obtener seis o menos caras en diez intentos podríamos indicar:
dbinom(c(0, 1, 2, 3, 4, 5, 6), size = 10, prob = 0.5)
## [1] 0.0009765625 0.0097656250 0.0439453125 0.1171875000 0.2050781250
## [6] 0.2460937500 0.2050781250
O alternativamente podríamos obtener cada uno de los valores representados en el gráfico mediante una sencilla fórmula:
prob <- NULL
for(k in 0:10){
prob <- c(prob,dbinom(k,10,0.5))
prob
}
prob
## [1] 0.0009765625 0.0097656250 0.0439453125 0.1171875000 0.2050781250
## [6] 0.2460937500 0.2050781250 0.1171875000 0.0439453125 0.0097656250
## [11] 0.0009765625
Ahora supongamos que la moneda ha sido trucada para favorecer que el resultado final sea cara. En este caso la probabilidad de obtener dicho resultado será superior, pongamos p = 0.6. Consecuentemente, suponiendo que de nuevo realizamos 10 lanzamientos, la probabilidad de obtener seis caras será superior con respecto al ejemplo anterior. Veamos en qué medida dicha probabilidad incrementa:
dbinom(x= 6, size = 10, prob = 0.6)
## [1] 0.2508227
Las distintas probabilidades en esta nueva situación se pueden representar gráficamente tal y como hemos hecho previamente:
data.frame(lanzam = 0:10, p = dbinom(x = 0:10, size = 10, prob = 0.6)) %>%
mutate(result = ifelse(lanzam == 6, "si", "no")) %>%
ggplot(aes(x = factor(lanzam), y = p, fill = result)) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 4,
vjust = 0) +
labs(title = "¿Cuál es la probabilidad de obtener seis veces `cara`?",
subtitle = "(p = 0,6)",
x = "Número de veces donde el resultado es `cara`",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))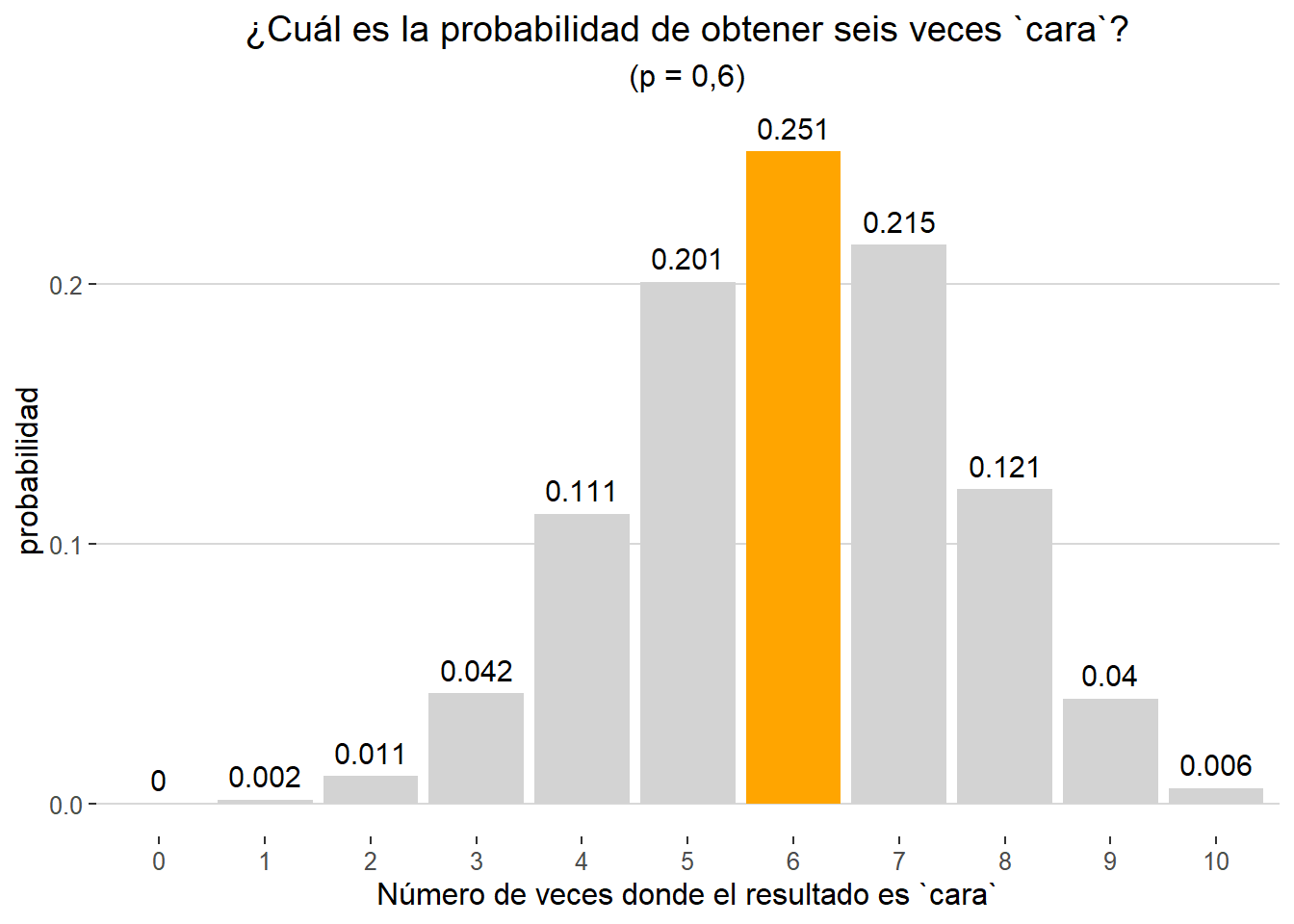
Ahora pongamos que nos interesa saber cuál es la probabilidad de obtener seis veces cara, pero en esta ocasión realizamos 12 lanzamientos en lugar de diez, y la probabilidad, por algún motivo, ha descendido a 0.4 (p = 0.4). Con estos nuevos parámetros comprobamos que la posibilidad de obtener el resultado mencionado se reduce a 0,1765
dbinom(x= 6, size = 12, prob = 0.4)
## [1] 0.1765791
Gráficamente comprobamos que, bajo las premisas establecidas, el resultado más probable es obtener 5 caras.
data.frame(lanzam = 0:12, p = dbinom(x = 0:12, size = 12, prob = 0.4)) %>%
mutate(result = ifelse(lanzam == 6, "si", "no")) %>%
ggplot(aes(x = factor(lanzam), y = p, fill = result)) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 4,
vjust = 0) +
labs(title = "¿Cuál es la probabilidad de obtener seis veces `cara`?",
subtitle = "(p = 0,4)",
x = "Número de veces donde el resultado es `cara`",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))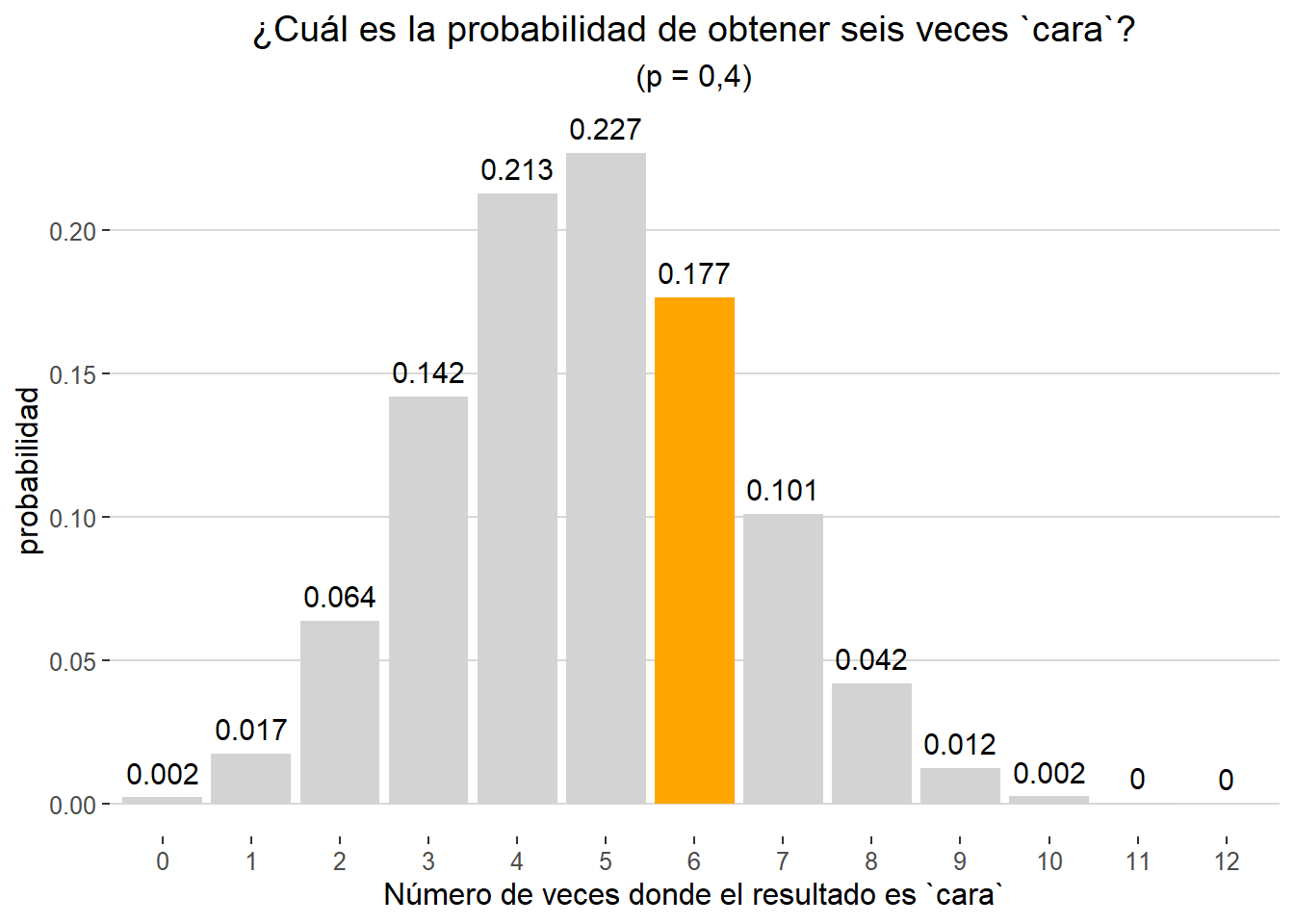
Hasta ahora hemos mostrado la aplicación de las funciones rbinom() y dbinom(). Otra de las cuatro funciones disponibles en {stats} es la función pbinom(), la función de distribución acumulada. Volvamos a nuestro primer ejemplo (10 lanzamientos y p = 0,5). Supongamos que nos interesa saber la probabilidad de obtener seis o menos veces cara. Para ello podríamos formular, por ejemplo, el siguiente código con el que sumamos la probabilidad de cada uno de los resultados de 0 a 6:
dbinom(0, size = 10, prob = 0.5) +
dbinom(1, size = 10, prob = 0.5) +
dbinom(2, size = 10, prob = 0.5) +
dbinom(3, size = 10, prob = 0.5) +
dbinom(4, size = 10, prob = 0.5) +
dbinom(5, size = 10, prob = 0.5) +
dbinom(6, size = 10, prob = 0.5)
## [1] 0.828125
No obstante, resulta más sencillo utilizar la función pnorm() para obtener de forma alternativa dicho resultado:
pbinom(q= 6, size= 10, prob= 0.5)
## [1] 0.828125
Gráficamente podemos representar el valor obtenido (valor acumulado) de la siguiente forma:
data.frame(lanzam = 0:10,
pmf = dbinom(x = 0:10, size = 10, prob = 0.5),
cdf = pbinom(q = 0:10, size = 10, prob = 0.5,
lower.tail = TRUE)) %>%
mutate(result = ifelse(lanzam <= 6, "si", "no")) %>%
ggplot(aes(x = factor(lanzam), y = cdf, fill = result)) +
geom_col() +
geom_text(aes(label = round(cdf,3), y = cdf + 0.005),
size = 4,
vjust = 0) +
labs(title = "¿Cuál es la probabilidad de obtener seis o menos veces (<=6) `cara`?",
subtitle = "(p = 0,5)",
x = "Número de veces donde el resultado es `cara`",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))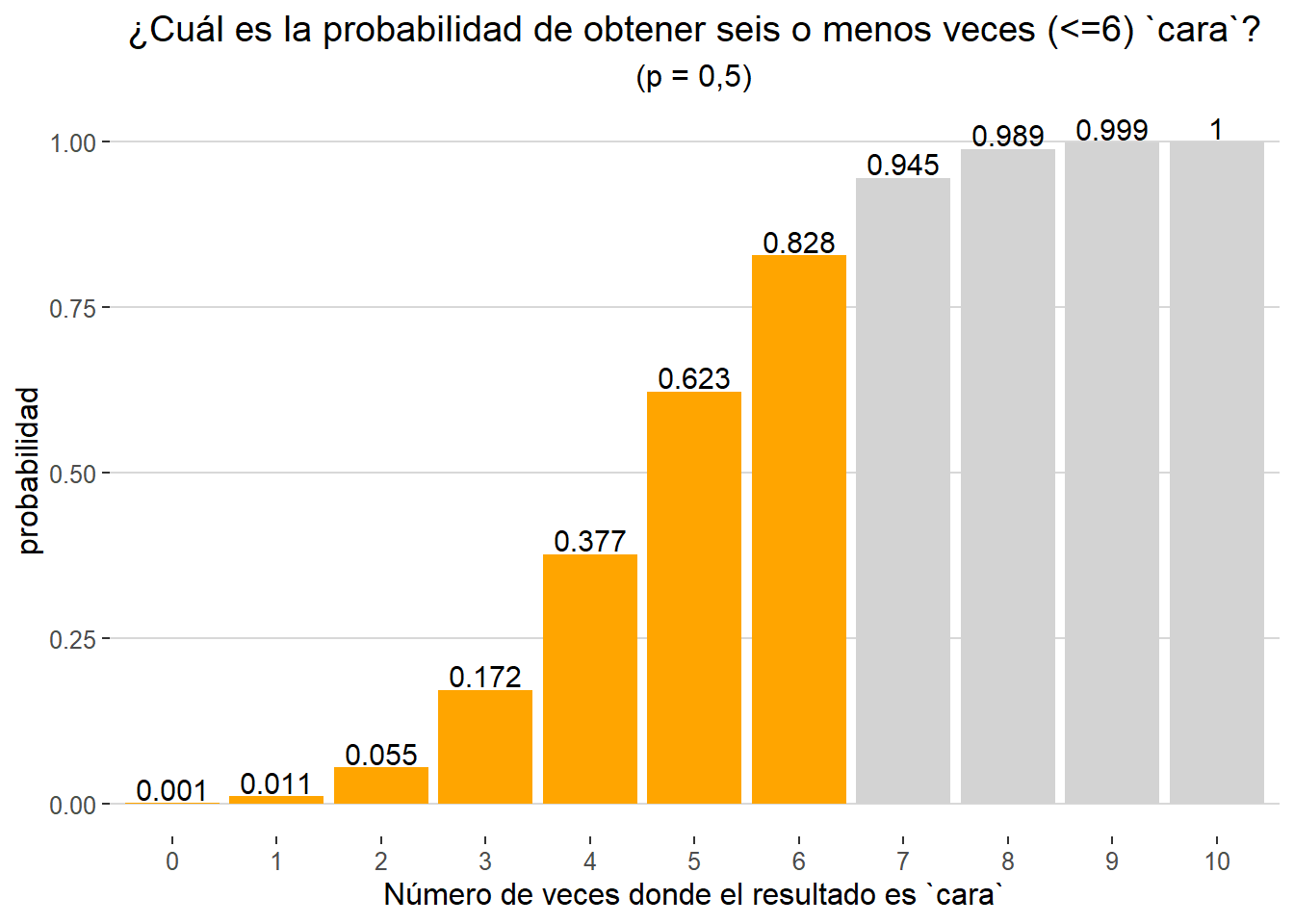
De forma análoga podemos estimar la probabilidad de obtener 6 o más veces cara con el comando lower.tail = TRUE.
pbinom(q=3, size= 10, p= 0.5, lower.tail= TRUE)
## [1] 0.171875
Gráficamente:
data.frame(lanzam = 0:10,
pmf = dbinom(x = 0:10, size = 10, prob = 0.5),
cdf = pbinom(q = -1:9, size = 10, prob = 0.5,
lower.tail = FALSE)) %>%
mutate(result = ifelse(lanzam >= 7, "si", "no")) %>%
ggplot(aes(x = factor(lanzam), y = cdf, fill = result)) +
geom_col() +
geom_text(aes(label = round(cdf,3), y = cdf + 0.005),
size = 4,
vjust = 0) +
labs(title = "¿Cuál es la probabilidad de obtener seis o más veces (>=6) `cara`?",
subtitle = "(p = 0,5)",
x = "Número de veces donde el resultado es `cara`",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))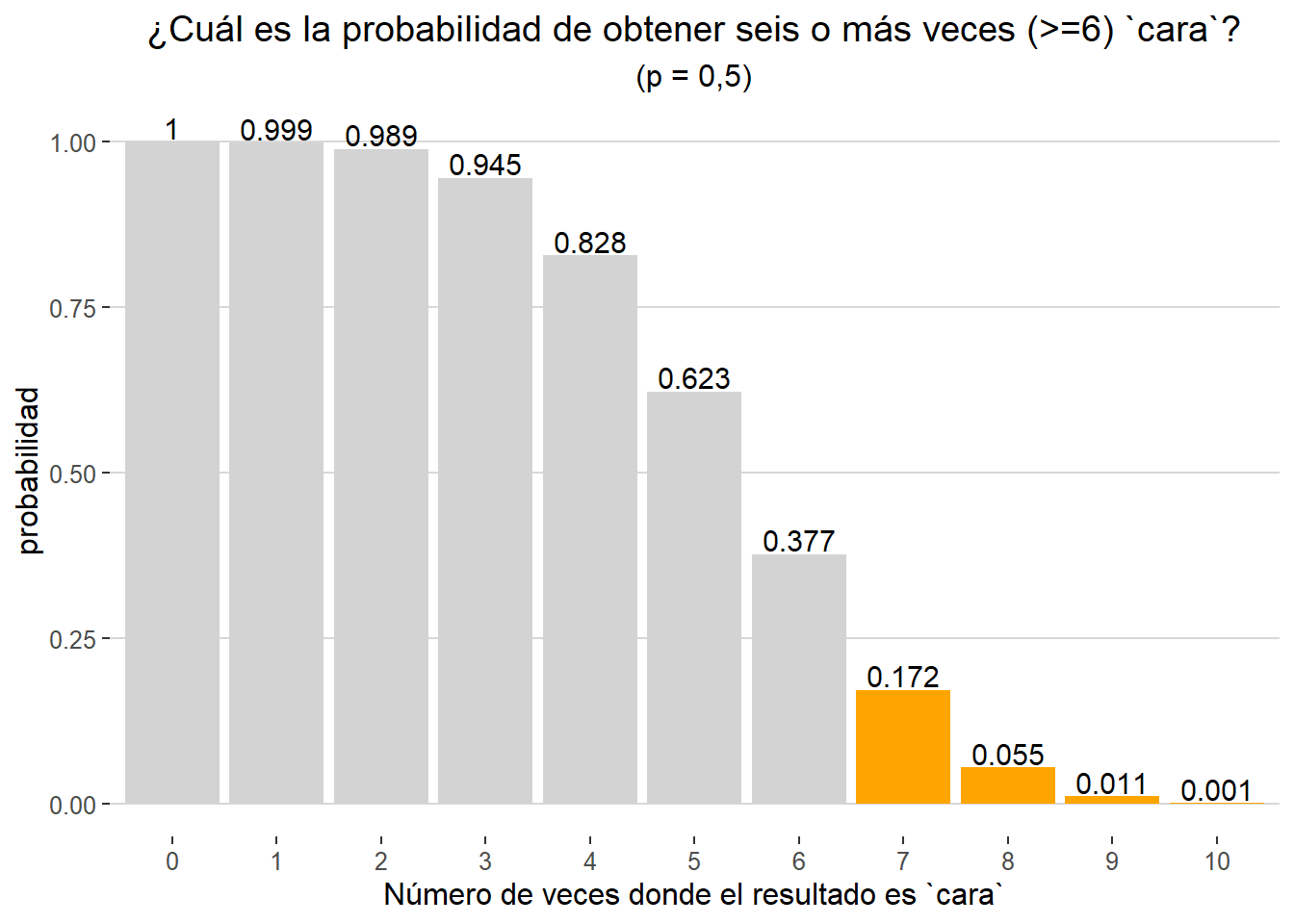
La última función que nos corresponde observar es qbinom(). Como se explicó al inicio del texto, esta función nos indica los cuantiles de la distribución. Por ejemplo, supongamos que queremos saber los cuantiles 10, 40, 60 y 80 de la distribución con la que llevamos trabajando a lo largo del post (size= 10, p=0.5)
qbinom(0.1, 10, 0.5)
## [1] 3
qbinom(0.4, 10, 0.5)
## [1] 5
qbinom(0.6, 10, 0.5)
## [1] 5
qbinom(0.8, 10, 0.5)
## [1] 6
Para obtener todos los cuantiles de la distribución podríamos formular el siguiente código:
qbinom(seq(0.1, 0.9, 0.1), 10, 0.5)
## [1] 3 4 4 5 5 5 6 6 7