Paquetes
library(dplyr)
library(ggplot2)
library(ggthemes)
library(reshape2)
library(ggpubr)
Introducción
Por lo general, el paquete {stats} de R (base R) que viene instalado por defecto incluye funciones para realizar operaciones asociadas a un gran número de distribuciones de probabilidad. La lista completa de las distribuciones incluidas en el paquete {stats} se obtiene indicando el siguiente comando: help("Distributions"), el cual nos devolverá la captura de pantalla que veremos a continuación. Se comprueba que el paquete {stats} incluye las distribuciones de probabilidad más comunes (binomial, chi-squared, exponential, F-distribution, normal distribution, etc.).
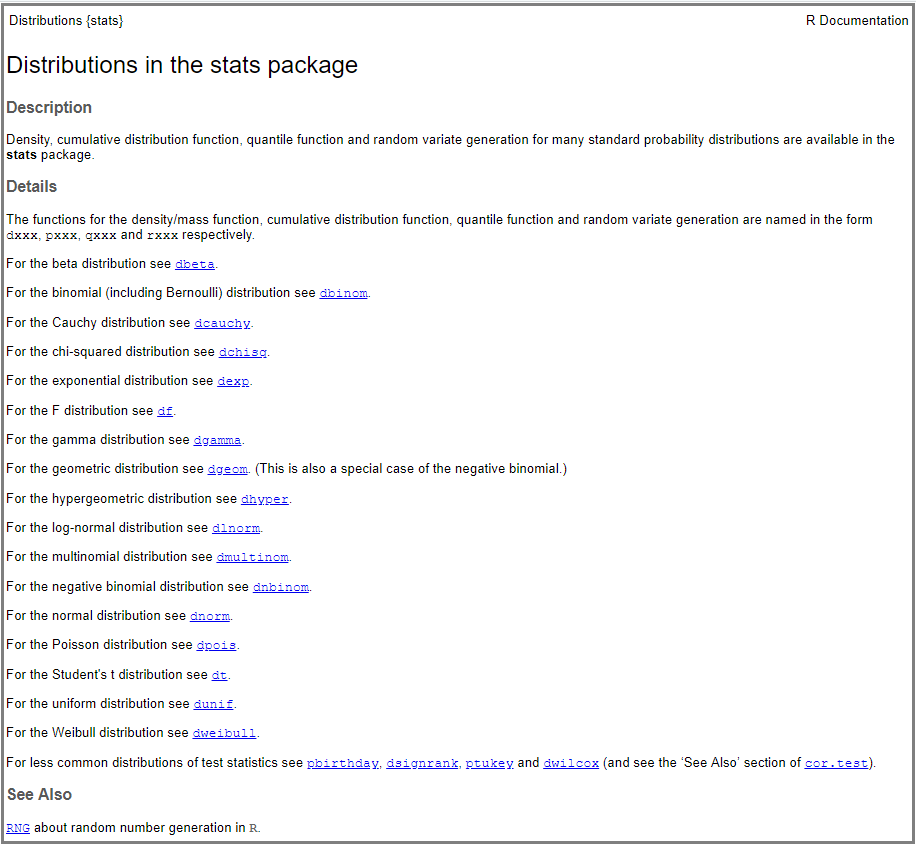
No obstante, téngase en cuenta que en CRAN podemos acceder a un gran número de paquetes donde se incluyen otras distribuciones más especializadas, u otros paquetes alternativos para trabajar con las distribuciones ya incluidas en {stats}. Una lista de dichos paquetes se puede consultar en el siguiente enlace.
En {stats} cada distribución de probabilidad tiene un nombre asignado y para cada una de ellas existen cuatro distintas funciones: función de densidad o de probabilidad (density), función de distribución (distribution function), función cuantílica (quantile function) y una función para la generación de números aleatorios (random variate generation), tal y como se explica en los detalles de la captura de pantalla mostrada previamente. Como se puede deducir de los respectivos nombres, la función density calcula la densidad (pdf) en un determinado valor, la función de distribución nos devuelve la distribución acumulada (cdf), la función cuantílica calcula el cuantil correspondiente a una determinada probabilidad y la última función genera un conjunto de valores aleatorios de una determinada distribución. Dichas funciones se indican anteponiendo los prefijos: d, p, q o r respectivamente al nombre asignado a cada distribución. Por ejemplo, para el caso de la distribución normal, que trataremos en este post, las funciones serán: dnorm(), pnorm(), qnorm() y rnorm()
Señalar que entre las distribuciones incluidas en {stats} podemos diferenciar entre distribuciones discretas y distribuciones continuas, donde las primeras no asumen valores intermedios entre dos números enteros mientras que las segundas si lo hacen. Entre las primeras distribuciones discretas encontramos, por ejemplo, la distribución binomial (binom), la distribución Poisson (pois) o la geométrica (geom). Entre las continuas tenemos la distribución normal (norm), la t-Student (t) o la distribución chi-cuadrado (chisq) entre otras.
Distribución Normal
La distribución normal es la distribución de probabilidad más común y utilizada y, por lo general, es la distribución que más tiende a ocurrir en fenómenos que ocurren en la naturaleza. De hecho, un ejemplo muy recurrido para explicar la distribución normal es el peso y la altura de las personas o los animales. La distribución normal se reconoce fácilmente por su forma de campana (bell shape) donde el centro de la curva representa la media. A esta curva se le denomina campana de Gauss, y como vemos en el gráfico siguiente es simétrica en ambos lados y asintótica (es decir, se acerca de continuo a la recta sin llegar a tocarla). Evidentemente, la mitad de los valores se situarán en la izquierda mientras que la otra mitad lo hará a la derecha.
La función de densidad de la distribución normal es la siguiente:

Por consiguiente, podríamos representar dicha función en R sustituyendo los valores en la fórmula. Para una distribución normal estándar de media poblacional 0 y desviación estándar 1 indicamos el siguiente código:
x <- seq(-4, 4, length = 100)
y <- 1/sqrt(2*pi)*exp(-x^2/2)
df <- data.frame(x,y)
ggplot(df, aes(x=x, y=y)) +
geom_line(color = "orange", size = 2) +
ylab("") +
labs(title = "Distribución Normal",
subtitle = "(sd=1)",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 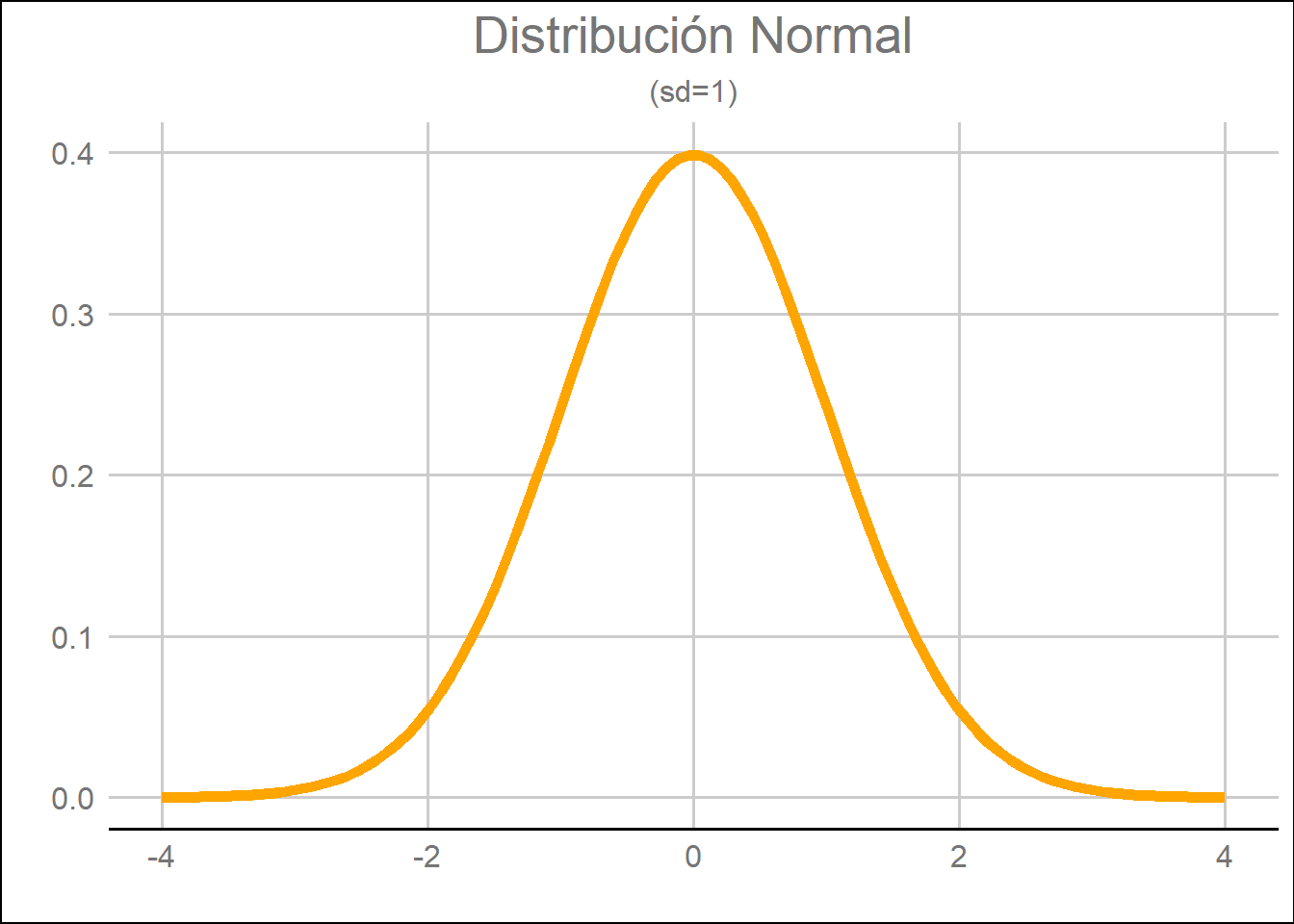
De acuerdo a la regla 68-95-99,7 , también llamada regla empírica, alrededor del 68% de los datos se encontrarán dentro de la primera desviación estándar, el 95% dentro de las dos primeras desviaciones estándar y el 99.7% dentro de las tres primeras. Es decir:
A <- ggplot(df, aes(x=x, y=y)) +
geom_line(color = "orange", size = 1) +
geom_area(aes(x= ifelse(x > -1 & x < 1, x, 0)), fill = "orange", alpha = 0.3) +
scale_y_continuous(limit=c(0, 0.4)) +
ylab("") +
labs(title = "68%",
subtitle = "",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))
B <- ggplot(df, aes(x=x, y=y)) +
geom_line(color = "orange", size = 1) +
geom_area(aes(x= ifelse(x > -2 & x < 2, x, 0)), fill = "orange", alpha = 0.3) +
scale_y_continuous(limit=c(0, 0.4)) +
ylab("") +
labs(title = "95%",
subtitle = "",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))
C <- ggplot(df, aes(x=x, y=y)) +
geom_line(color = "orange", size = 1) +
geom_area(aes(x= ifelse(x > -3 & x < 3, x, 0)), fill = "orange", alpha = 0.3) +
scale_y_continuous(limit=c(0, 0.4)) +
ylab("") +
labs(title = "99,7%",
subtitle = "",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))
ggarrange(A,B,C, ncol = 3, nrow = 1)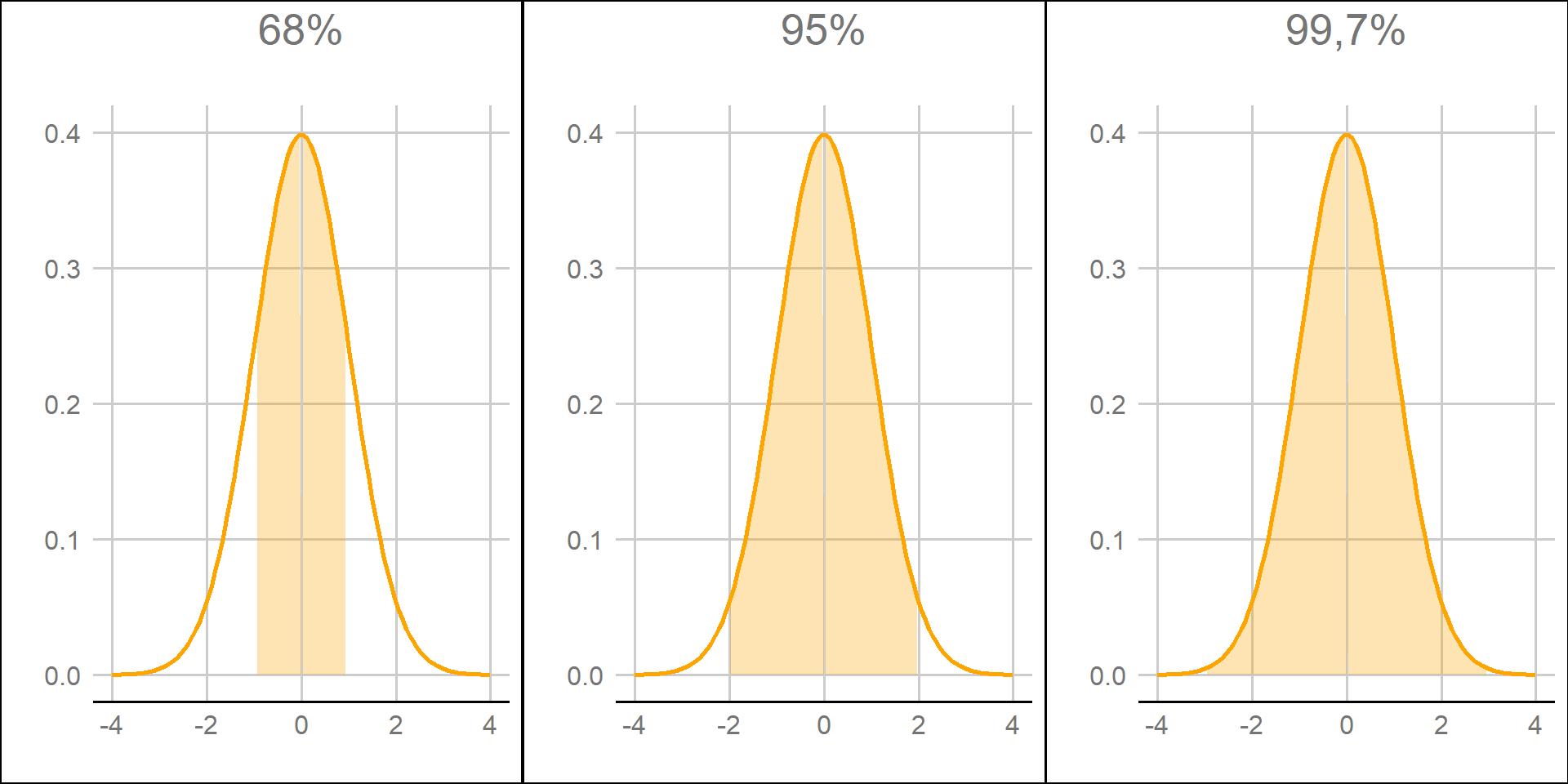
El paquete {stats} nos facilita el trabajo ofreciéndonos la posibilidad de utilizar la función dnorm() para representar la distribución de probabilidad. Consecuentemente, podemos representar gráficamente la misma distribución estándar normal (con media poblacional = 0 y desviación estándar = 1) de la siguiente forma:
data.frame(x=c(-3,3)) %>%
ggplot(aes(x = x)) +
stat_function(fun = dnorm, n = 100, args = list(mean = 0, sd = 1),
color = "orange",
size = 2) +
ylab("") +
labs(title = "Distribución Normal",
subtitle = "(sd = 1)",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 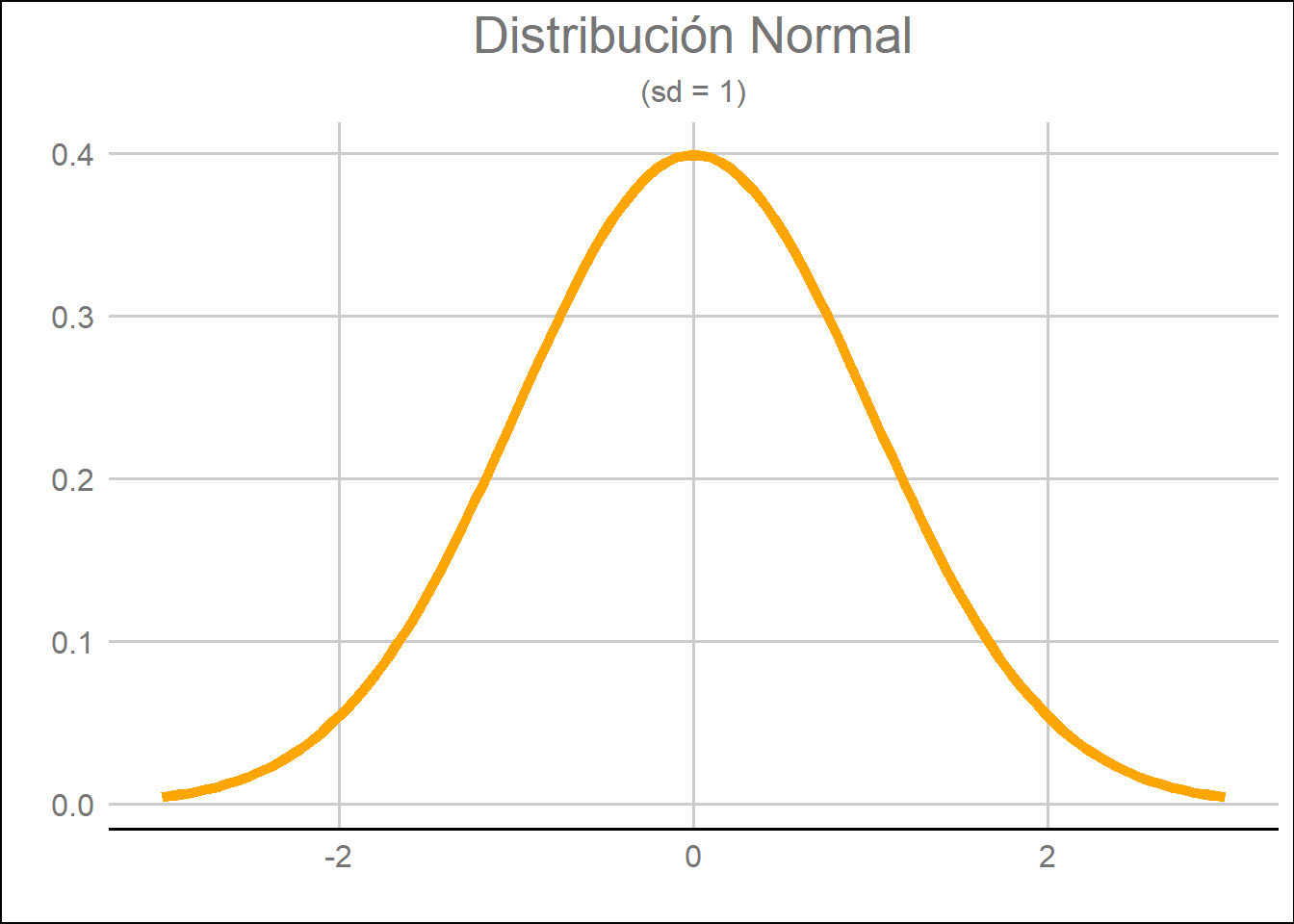
Comprobamos que la distribución normal depende fundamentalmente de dos parámetros: la media poblacional (llamada a veces esperanza) y la desviación estándar. Podemos observar gráficamente en cómo se traduce en la distribución las modificaciones realizadas en dichos parámetros:
Si modificamos la media poblacional:
data.frame(x=c(-4,4)) %>%
ggplot(aes(x = x)) +
stat_function(fun = dnorm, n = 100, args = list(mean = 0, sd = 1), color = "orange", size = 2) +
stat_function(fun = dnorm, n = 100, args = list(mean = 1, sd = 1), color = "lightblue", size = 1.5) +
stat_function(fun = dnorm, n = 100, args = list(mean = -1, sd = 1), color = "limegreen", size = 1.5) +
ylab("") +
scale_y_continuous(breaks = NULL) +
labs(title = "Distribución Normal",
subtitle = "(Media Poblacional: -1, 0, 1)",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 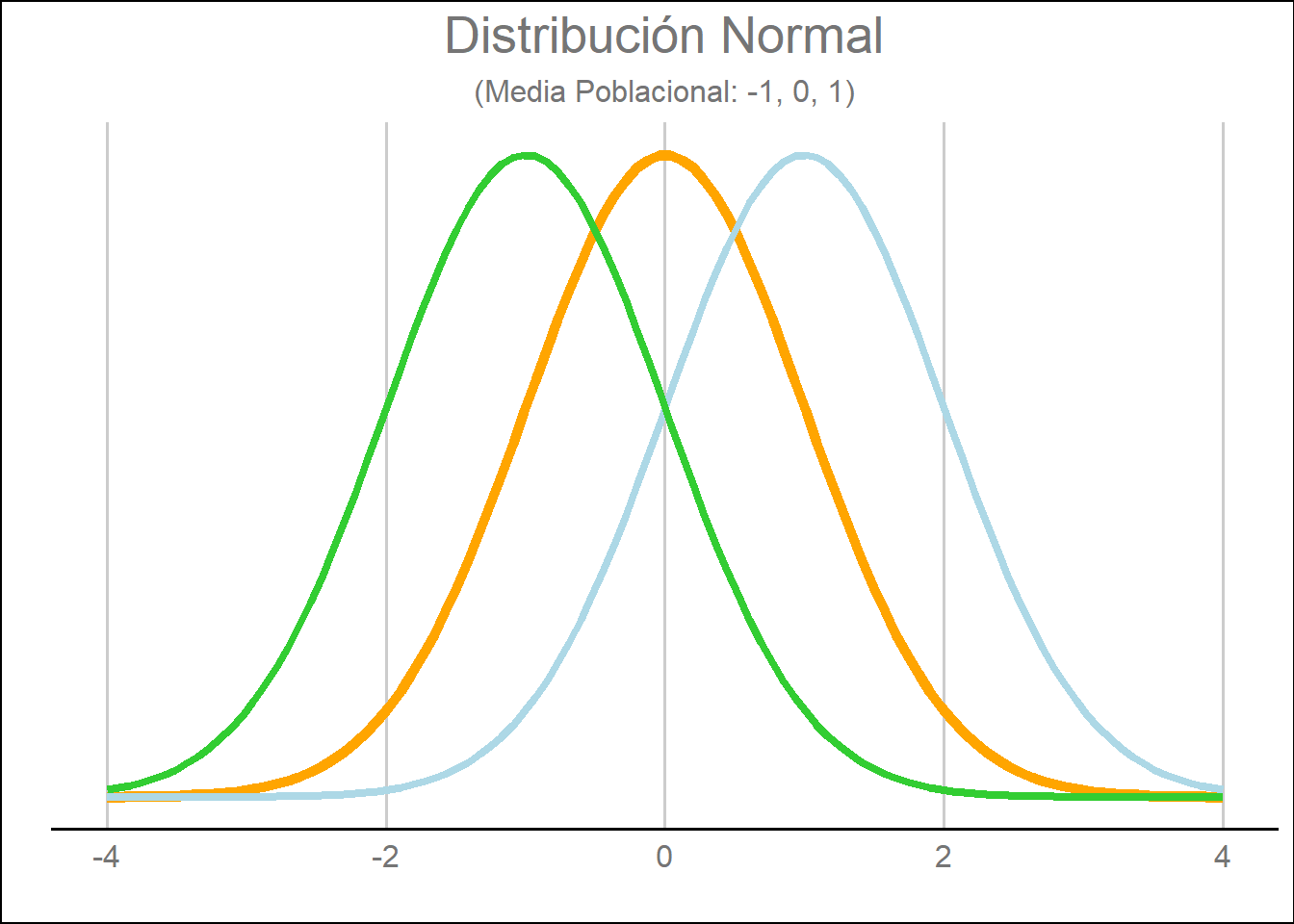
Si modificamos la desviación estándar:
data.frame(x=c(-4,4)) %>%
ggplot(aes(x = x)) +
stat_function(fun = dnorm, n = 100, args = list(mean = 0, sd = 1), color = "orange", size = 2) +
stat_function(fun = dnorm, n = 100, args = list(mean = 0, sd = 2), color = "lightblue", size = 1.5) +
stat_function(fun = dnorm, n = 100, args = list(mean = 0, sd = 0.5), color = "limegreen", size = 1.5) +
ylab("") +
labs(title = "Distribución Normal",
subtitle = "(sd = 0.5, 1, 2)",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 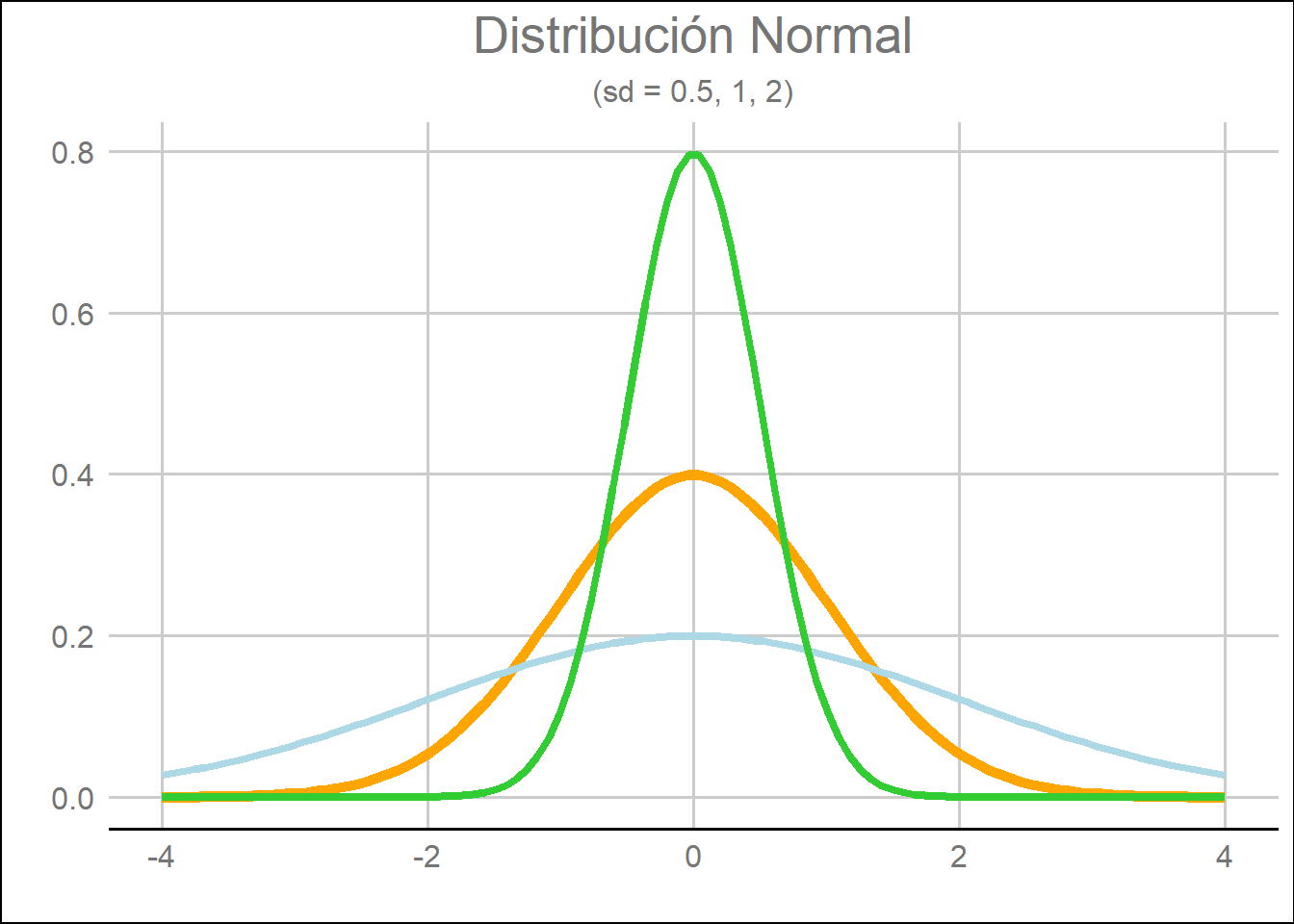
Podemos obtener la densidad en diferentes posiciones de la distribución con la función dnorm(). Si la media poblacional o la desviación estándar no se especifican, {stats} asume que los valores por defecto son 0 y 1 respectivamente.
dnorm(x = c(-1.5, 0, 1.5))
## [1] 0.1295176 0.3989423 0.1295176
dnorm(x = c(-1.5, 0, 1.5), mean = 0, sd = 2)
## [1] 0.1505687 0.1994711 0.1505687
dnorm(x = c(-1.5, 0, 1.5), mean = 0, sd = 0.5)
## [1] 0.008863697 0.797884561 0.008863697
Como ya expusimos en los post donde explicábamos la distribución binomial y la distribución de Poisson, {stats} nos ofrece una función para calcular la probabilidad acumulada que se construye sumando el prefijo p al nombre asignado a cada distribución. Por consiguiente, para obtener la distribución acumulada de una distribución normal utilizaremos la función pnorm(). Gráficamente la distribución acumulada de la distribución de probabilidad estándar será la siguiente:
data.frame(x=c(-3,3)) %>%
ggplot(aes(x = x)) +
stat_function(fun = pnorm, n = 100, args = list(mean = 0, sd = 1),
color = "orange",
size = 2) +
ylab("") +
labs(title = "Distribución Normal Acumulada",
subtitle = "(sd = 1)",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 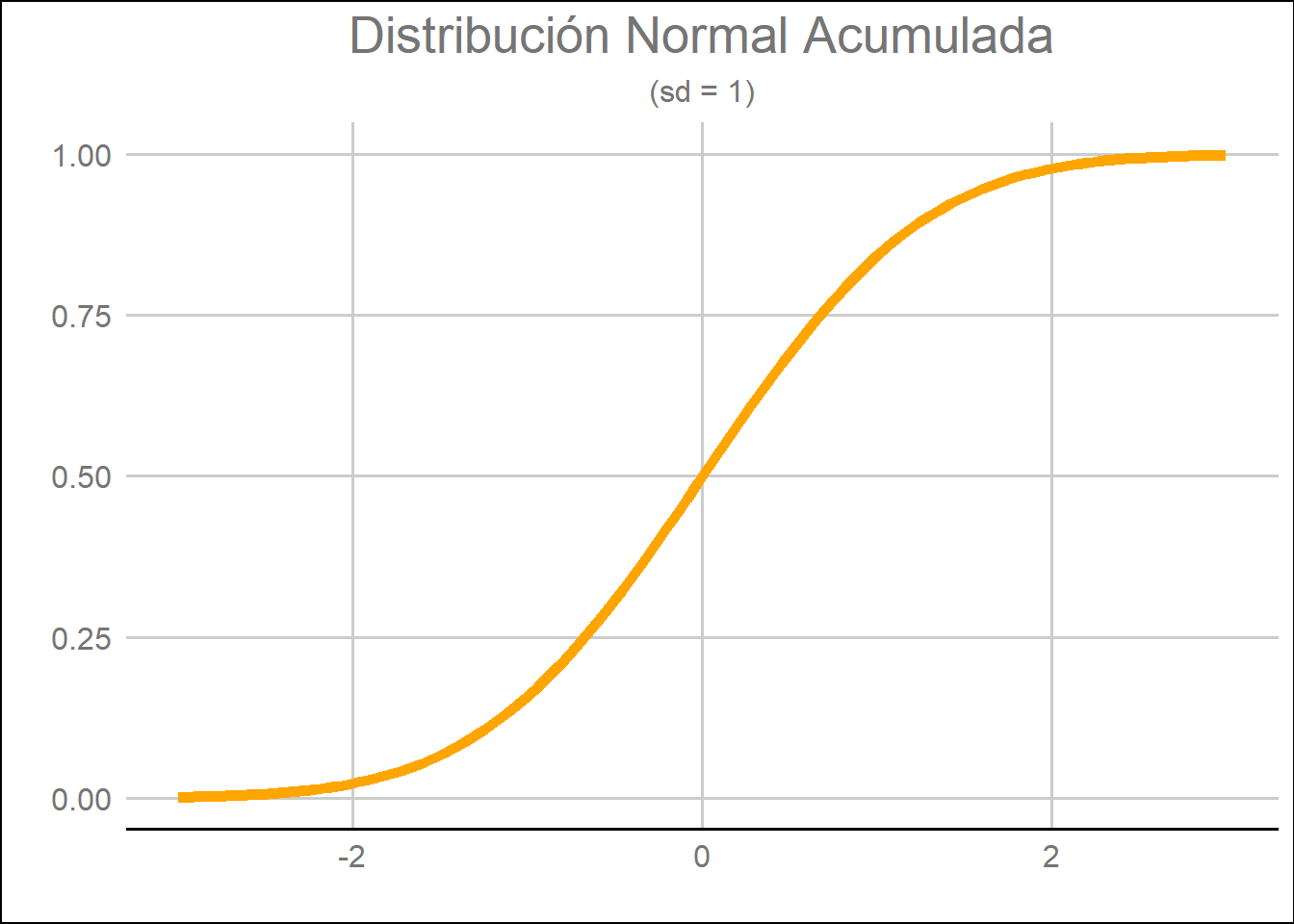
Y a modo de comparación, la distribución acumulada de varias distribuciones de probabilidad que presentan diferentes desviaciones estándar serán:
data.frame(x=c(-3,3)) %>%
ggplot(aes(x = x)) +
stat_function(fun = pnorm, n = 100, args = list(mean = 0, sd = 1), color = "orange", size = 2) +
stat_function(fun = pnorm, n = 100, args = list(mean = 0, sd = 2), color = "lightblue", size = 1.5) +
stat_function(fun = pnorm, n = 100, args = list(mean = 0, sd = 0.5), color = "limegreen", size = 1.5) +
ylab("") +
labs(title = "Distribución Normal Acumulada",
subtitle = "(sd = 0.5, 1, 2)",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 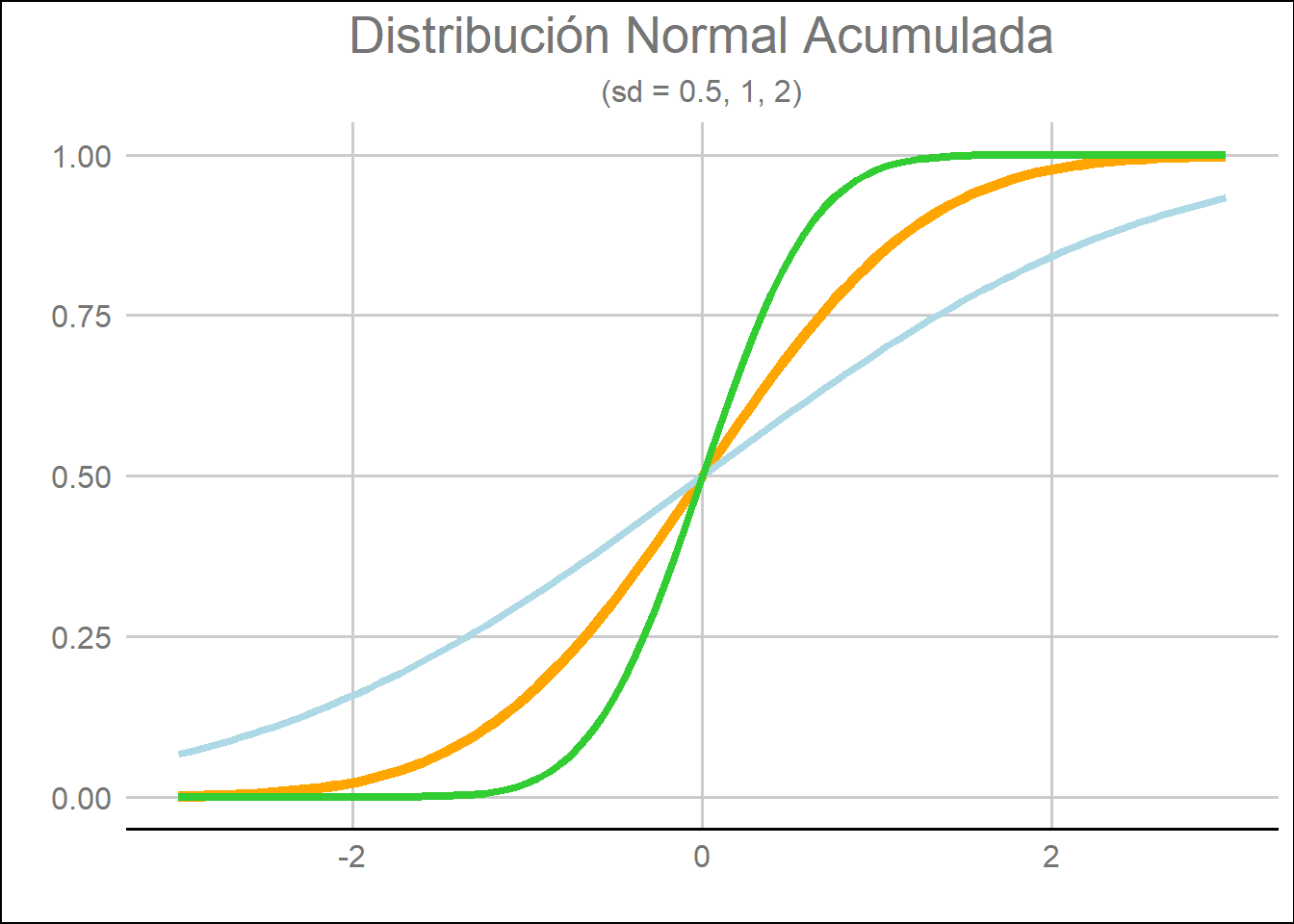
Veamos algún ejemplo práctico. Supongamos que nos encontramos en el hospital de Txagurritxu (en Vitoria-Gasteiz) y nos proponemos examinar el peso de 500 bebés en el momento de cumplir un año. EL peso medio, en kilos es de 9,5 kilos y la desviación estándar es de 1.2 kilos. Suponiendo que el peso se distribuye normalmente nos preguntamos:
1. ¿Qué probabilidad hay de que los bebés pesen menos de 9,5 kilos?
ejemplo_mean <- 9.5
ejemplo_sd <- 1.2
ejemplo_x <- 9
pnorm(q = ejemplo_x, mean = ejemplo_mean, sd = ejemplo_sd, lower.tail = TRUE)
## [1] 0.3384611
data.frame(x= 5:1500 / 100,
prob = pnorm (q = 5:1500 / 100,
mean = ejemplo_mean,
sd = ejemplo_sd,
lower.tail = TRUE)) %>%
mutate(cdf = ifelse(x > 0 & x <= ejemplo_x, prob, 0)) %>%
ggplot() +
geom_line(aes(x=x, y= prob), color = "orange", size = 2) +
geom_area(aes(x=x, y= cdf), fill = "orange", alpha = 0.3) +
ylab("") +
labs(title = "Probabilidad de pesar menos de 9 kilos",
subtitle = bquote('('~mu==.(ejemplo_mean)~','~sigma^{2}==.(ejemplo_sd)^{2}~')'),
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 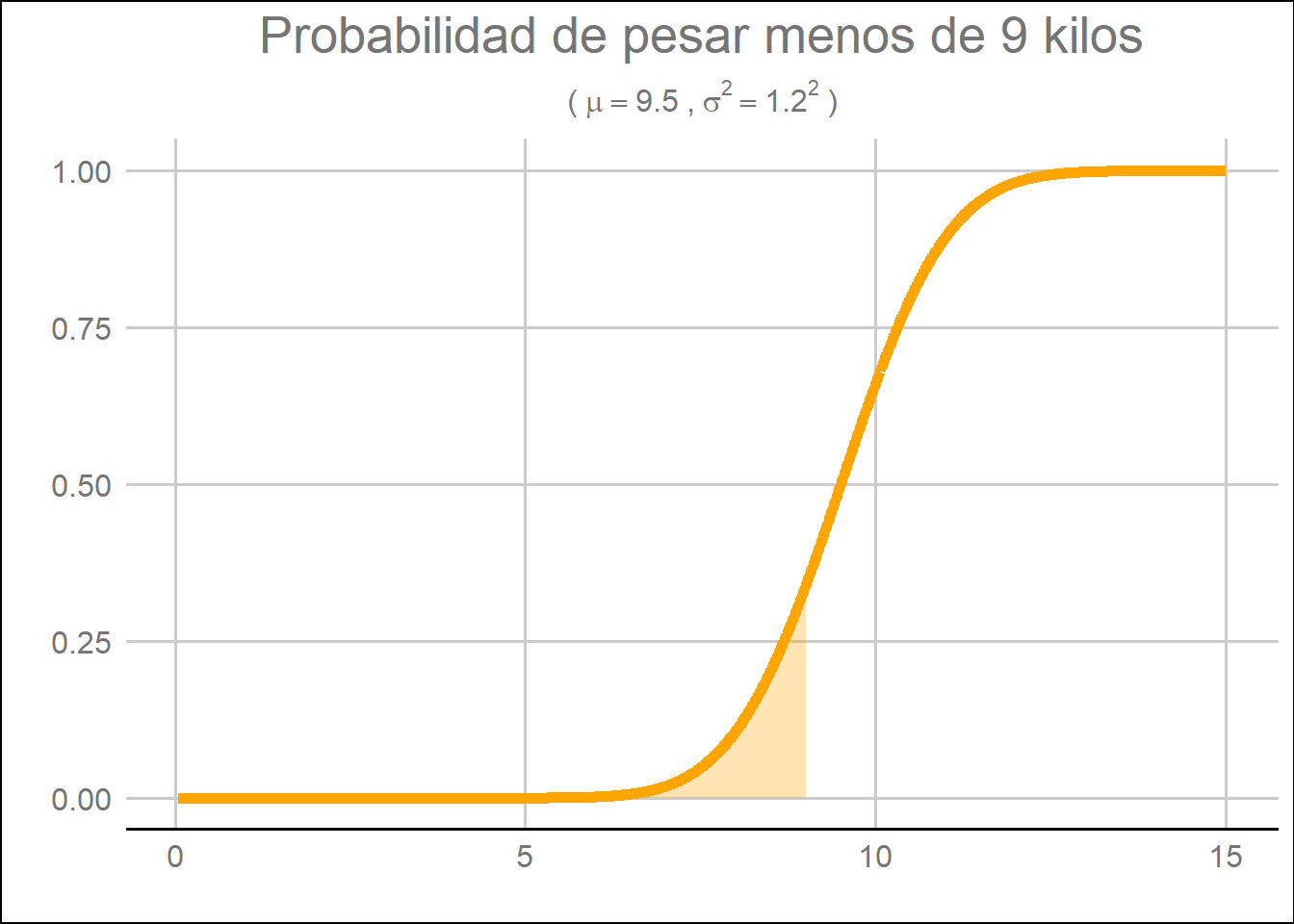
2. ¿Qué probabilidad hay de que los bebés pesen más de 12 kilos?
ejemplo_mean <- 9.5
ejemplo_sd <- 1.2
ejemplo_x <- 11
pnorm(q = ejemplo_x, mean = ejemplo_mean, sd = ejemplo_sd, lower.tail = FALSE)
## [1] 0.1056498
data.frame(x= 5:1500 / 100,
prob = pnorm (q = 5:1500 / 100,
mean = ejemplo_mean,
sd = ejemplo_sd,
lower.tail = TRUE)) %>%
mutate(cdf = ifelse(x > ejemplo_x & x < 20, prob, 0)) %>%
ggplot() +
geom_line(aes(x=x, y= prob), color = "orange", size = 2) +
geom_area(aes(x=x, y= cdf), fill = "orange", alpha = 0.3) +
ylab("") +
labs(title = "Probabilidad de pesar más de 11 kilos",
subtitle = bquote('('~mu==.(ejemplo_mean)~','~sigma^{2}==.(ejemplo_sd)^{2}~')'),
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 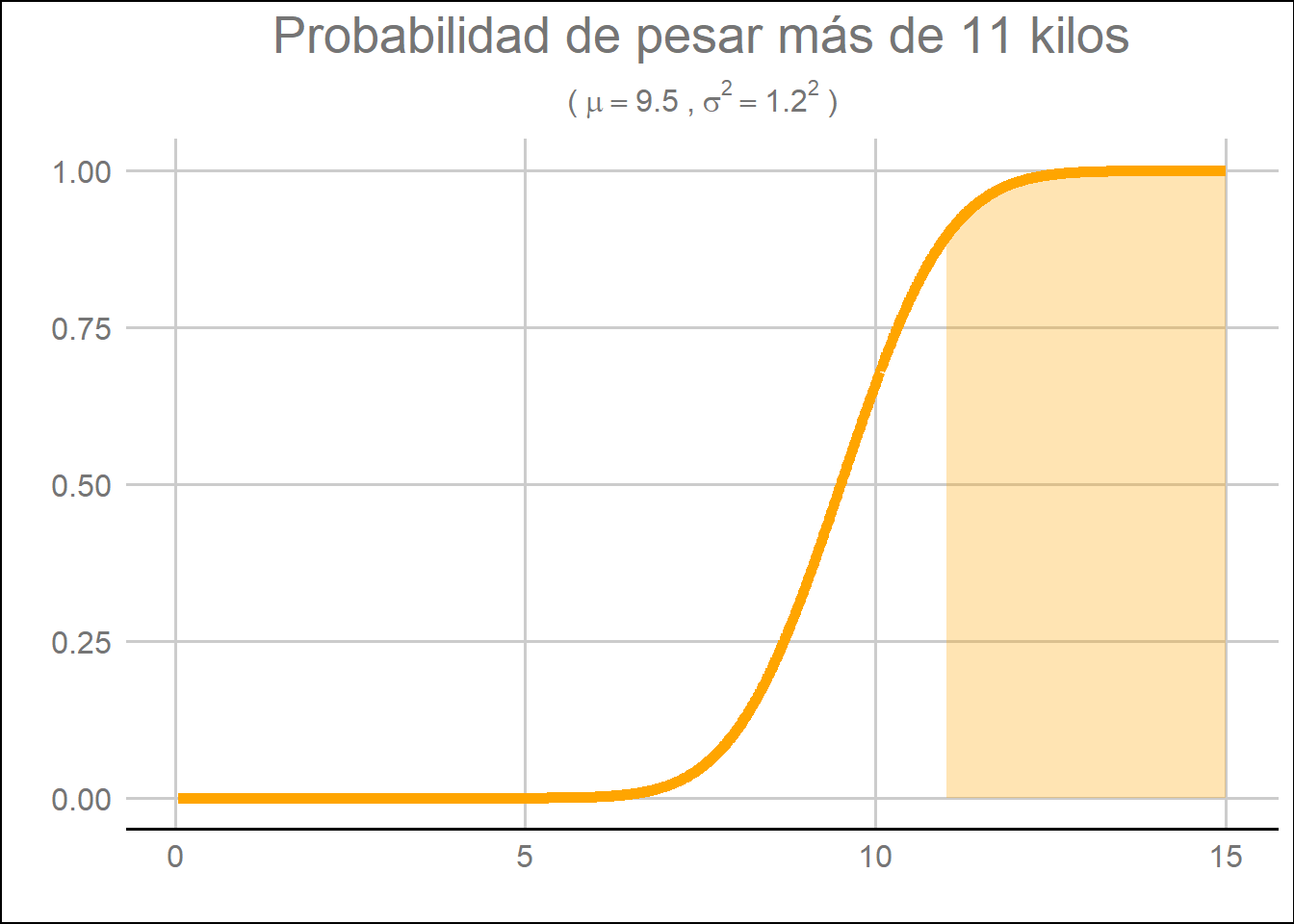
3. ¿Qué probabilidad hay de que un bebé pese entre 9 y 11 kilos?
ejemplo_mean <- 9.5
ejemplo_sd <- 1.2
ejemplo_x_A <- 9
ejemplo_x_B <- 11
pnorm(q = ejemplo_x_B, mean = ejemplo_mean, sd = ejemplo_sd, lower.tail = TRUE) - pnorm(q = ejemplo_x_A, mean = ejemplo_mean, sd = ejemplo_sd, lower.tail = TRUE)
## [1] 0.5558891
data.frame(x= 5:1500 / 100,
prob = pnorm (q = 5:1500 / 100,
mean = ejemplo_mean,
sd = ejemplo_sd,
lower.tail = TRUE)) %>%
mutate(cdf = ifelse(x > ejemplo_x_A & x <= ejemplo_x_B, prob, 0)) %>%
ggplot() +
geom_line(aes(x=x, y= prob), color = "orange", size = 2) +
geom_area(aes(x=x, y= cdf), fill = "orange", alpha = 0.3) +
ylab("") +
labs(title = "Probabilidad de pesar entre 9 y 11 kilos",
subtitle = bquote('('~mu==.(ejemplo_mean)~','~sigma^{2}==.(ejemplo_sd)^{2}~')'),
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 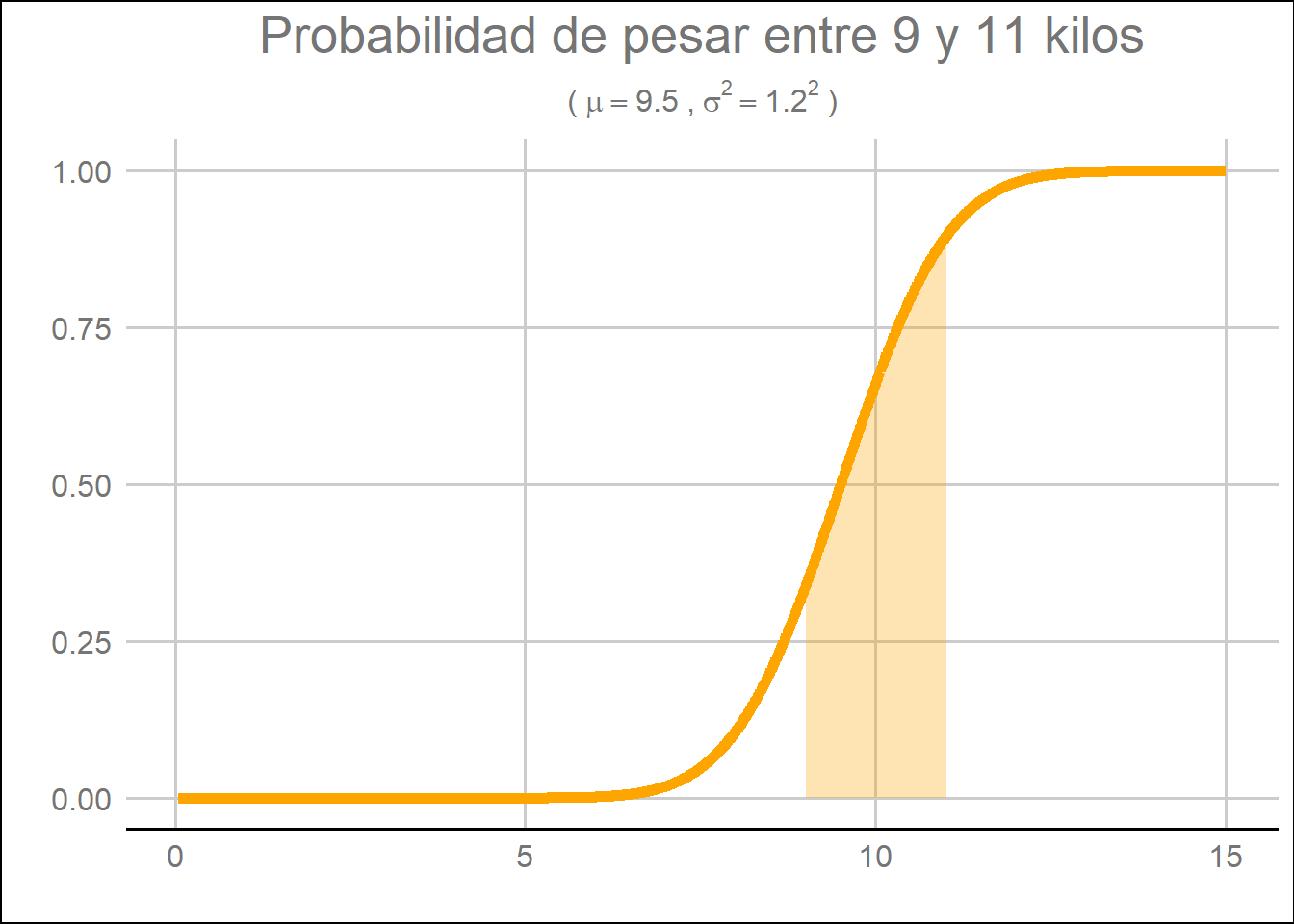
Otra de las funciones que incluye el paquete {stats} es la función qnorm(). Esta función nos permite identificar los cuantiles dentro de la distribución. Pongamos por ejemplo que tenemos una distribución normal de media poblacional = 65 y desviación estándar de 8. Nos interesa identificar los puntos de corte en el cuantil 40 y el cuantil 80. Con qnorm() podemos fácilmente identificar dichos puntos de corte de la siguiente forma:
ejemplo_mean <- 65
ejemplo_sd <- 8
ejemplo_x_A <- .40
ejemplo_x_B <- .80
qnorm(p = ejemplo_x_A, mean = ejemplo_mean, sd = ejemplo_sd, lower.tail = TRUE)
## [1] 62.97322
qnorm(p = ejemplo_x_B, mean = ejemplo_mean, sd = ejemplo_sd, lower.tail = TRUE)
## [1] 71.73297
Gráficamente podemos representar el rango entre dichos cuantiles de la siguiente forma:
data.frame(x= 0:1000 / 10,
prob = pnorm (q = 0:1000 / 10,
mean = ejemplo_mean,
sd = ejemplo_sd,
lower.tail = TRUE)) %>%
mutate(cdf = ifelse(prob > ejemplo_x_A & prob <= ejemplo_x_B, prob, 0)) %>%
ggplot() +
geom_line(aes(x=x, y= prob), color = "orange", size = 2) +
geom_area(aes(x=x, y= cdf), fill = "orange", alpha = 0.3) +
ylab("") +
labs(title = "Rango entre el percentil 40 y el 80",
subtitle = bquote('('~mu==.(ejemplo_mean)~','~sigma^{2}==.(ejemplo_sd)^{2}~')'),
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 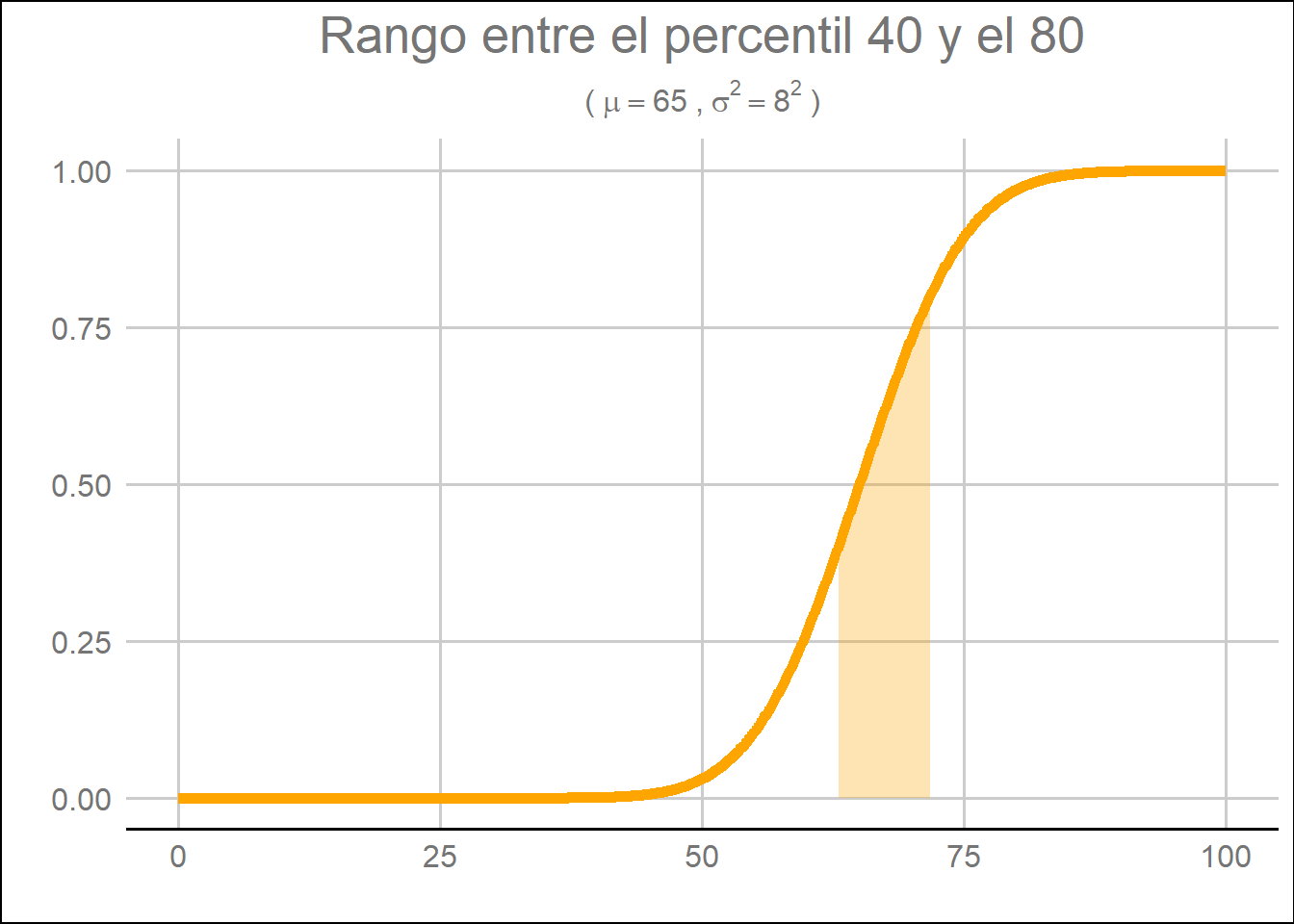
Como ya hemos visto en otras distribuciones de probabilidad, {stats} proporciona una función para cada una de ellas que permite generar series aleatorias. Supongamos que, por ejemplo, queremos generar una serie aleatoria con distribución normal que represente la altura de varios olivos. Supongamos que el olivo tiene una altura promedio de 7 metros y una desviación estándar de 2. Entonces una posible serie de 100 observaciones (100 olivos) sería:
olivos <- rnorm(100, mean = 7, sd = 2)
olivos
## [1] 7.447822 8.862252 8.012767 6.015085 6.116325 6.940981 6.509739
## [8] 8.624527 10.419245 7.184027 6.545747 7.357093 6.077629 7.618850
## [15] 6.377975 1.667454 4.438628 7.895856 11.987341 9.463488 8.774685
## [22] 7.506186 6.727438 7.868289 4.284053 8.960383 7.376603 8.112697
## [29] 5.855613 7.463884 6.773419 6.743569 8.079300 7.095979 8.035681
## [36] 7.002033 5.361159 5.911612 9.289258 10.609462 6.229950 5.529456
## [43] 6.398546 5.427150 5.545297 6.917146 5.089598 5.060880 7.080442
## [50] 4.004081 4.389419 7.044577 8.781785 8.328860 2.589527 11.742978
## [57] 6.634681 6.814359 6.529128 6.421224 10.965851 4.180204 9.426570
## [64] 6.631233 5.465652 7.168527 6.034899 6.216268 6.069034 7.622364
## [71] 10.701774 3.899802 6.646301 3.246650 8.121556 3.776163 8.384944
## [78] 8.952881 7.171299 7.088804 5.098420 7.000889 6.666149 4.086383
## [85] 5.831089 11.123508 6.854681 8.100347 9.566048 6.022672 6.362585
## [92] 8.415924 7.063273 8.556221 5.929733 9.762756 8.846109 7.075678
## [99] 7.955708 8.564420
Supongamos que por su parte, la altura promedio de la encina es de 18 metros, con una desviación estándar de 3.5. Una posible serie de 100 observaciones de encinas sería:
encinas <- rnorm(100, mean = 18, sd = 3.5)
encinas
## [1] 12.198601 17.943230 17.624426 16.306583 12.486911 22.499270 26.165300
## [8] 19.030625 18.872527 14.632699 18.365214 24.459588 20.580038 21.978510
## [15] 21.896338 19.682628 22.391515 16.960361 17.137484 18.576590 20.830747
## [22] 24.719254 24.771126 17.526103 21.470360 15.263730 13.957590 12.159857
## [29] 19.806102 12.818474 17.289912 16.636266 18.380416 6.170506 14.417388
## [36] 22.136893 17.199238 19.437331 20.478228 17.320479 17.937537 16.375649
## [43] 13.142968 24.302430 17.654529 24.697839 21.892320 18.189588 17.864458
## [50] 17.091650 18.129387 25.350296 19.583298 11.585549 20.949610 18.460982
## [57] 24.740307 18.239229 22.347152 23.925054 14.875909 18.616325 16.214885
## [64] 11.793149 24.709852 20.451835 12.632239 18.073625 13.648707 12.595406
## [71] 13.088400 14.724364 24.610770 10.269685 15.474307 21.653787 23.664017
## [78] 16.933876 19.364851 22.063520 17.518074 22.898675 19.322889 17.364631
## [85] 21.870054 12.848930 11.799025 16.664127 15.172061 17.192764 18.986511
## [92] 21.448750 10.622074 12.533871 15.643834 16.251399 13.167920 19.391868
## [99] 13.893432 15.213315
Podemos crear un dataframe con las alturas de los 100 olivos y las 100 encinas de la siguiente forma:
df <- data.frame(olivos, encinas)
df_arbol <-as_tibble(melt(df))
Con la función geom_density() podemos fácilmente representar en un gráfico las distribuciones de los olivos y las encinas. En principio, la distribución de la altura de los olivos debería tener una media de aproximadamente 7 y desviación estándar de 2 mientras que la distribución de las encinas debería tener una media aproximada de 18 y una desviación estándar de 3.5. Comprobamos en el gráfico que dichos parámetros se cumplen.
mean_olivo = 7
mean_encina = 18
sd_olivo = 2
sd_encina = 3.5
ggplot(df_arbol, aes(x= value, fill = variable, color = variable)) +
geom_density(alpha = 0.4,size = 1.5) +
scale_fill_manual(values = c("orange", "darkgrey")) +
scale_color_manual(values = c("orange", "darkgrey")) +
ylab("") +
labs(title = "Distribuciones: olivos y encinas",
subtitle = "",
x = "",
y = "") +
guides(fill = FALSE) +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 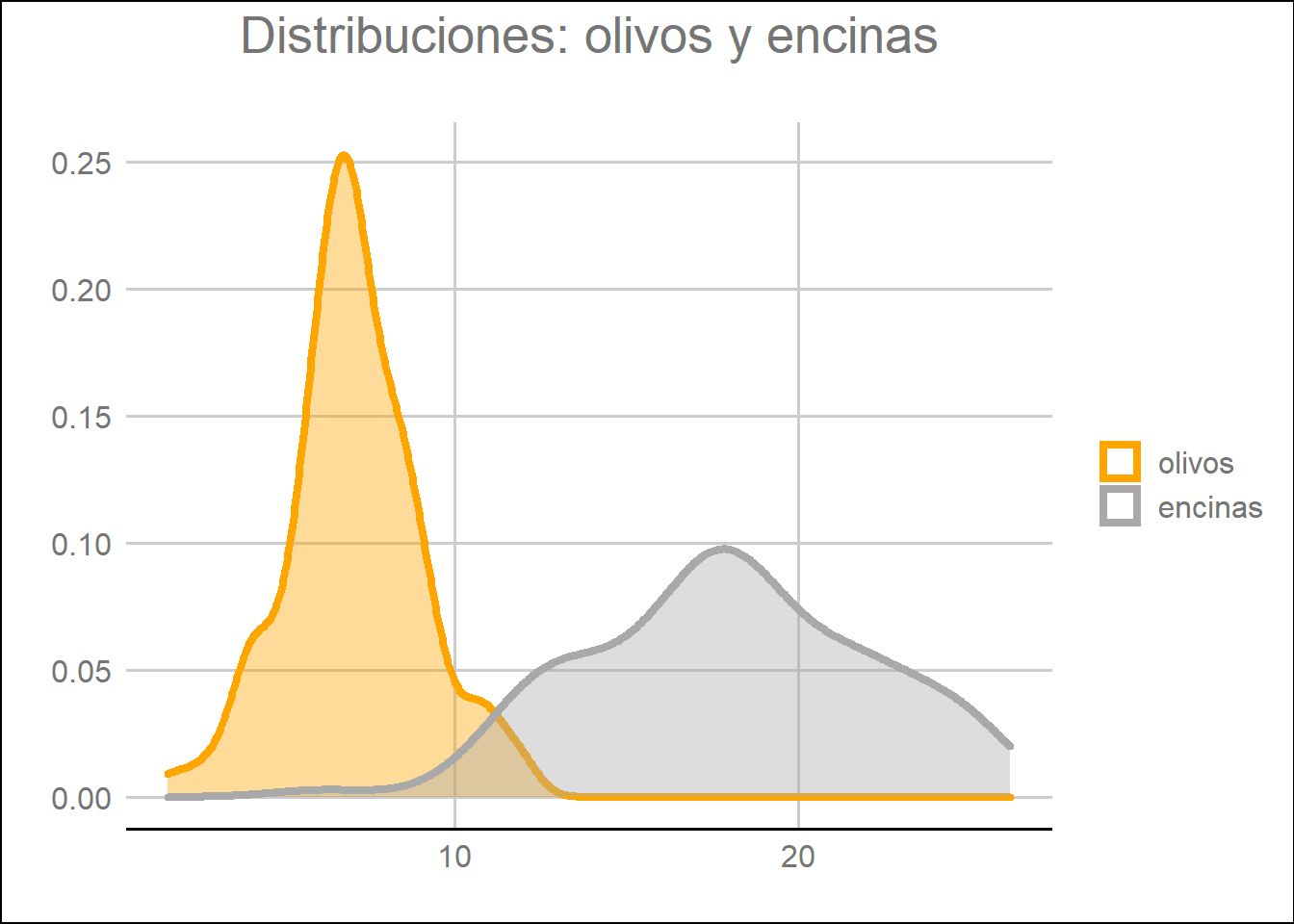
Podemos observar en mayor detalle las características de la distribución de los árboles mediante el uso de un histograma utilizando la función geom_histogram() del paquete {ggplot2}. De esta forma podemos
ggplot(df_arbol, aes(x= value, fill = variable, color = variable)) +
geom_histogram(alpha = 0.4, bins = 30) +
scale_fill_manual(values = c("orange", "darkgrey")) +
scale_color_manual(values = c("orange", "darkgrey")) +
ylab("") +
labs(title = "Distribuciones: olivos y encinas",
subtitle = "",
x = "",
y = "") +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 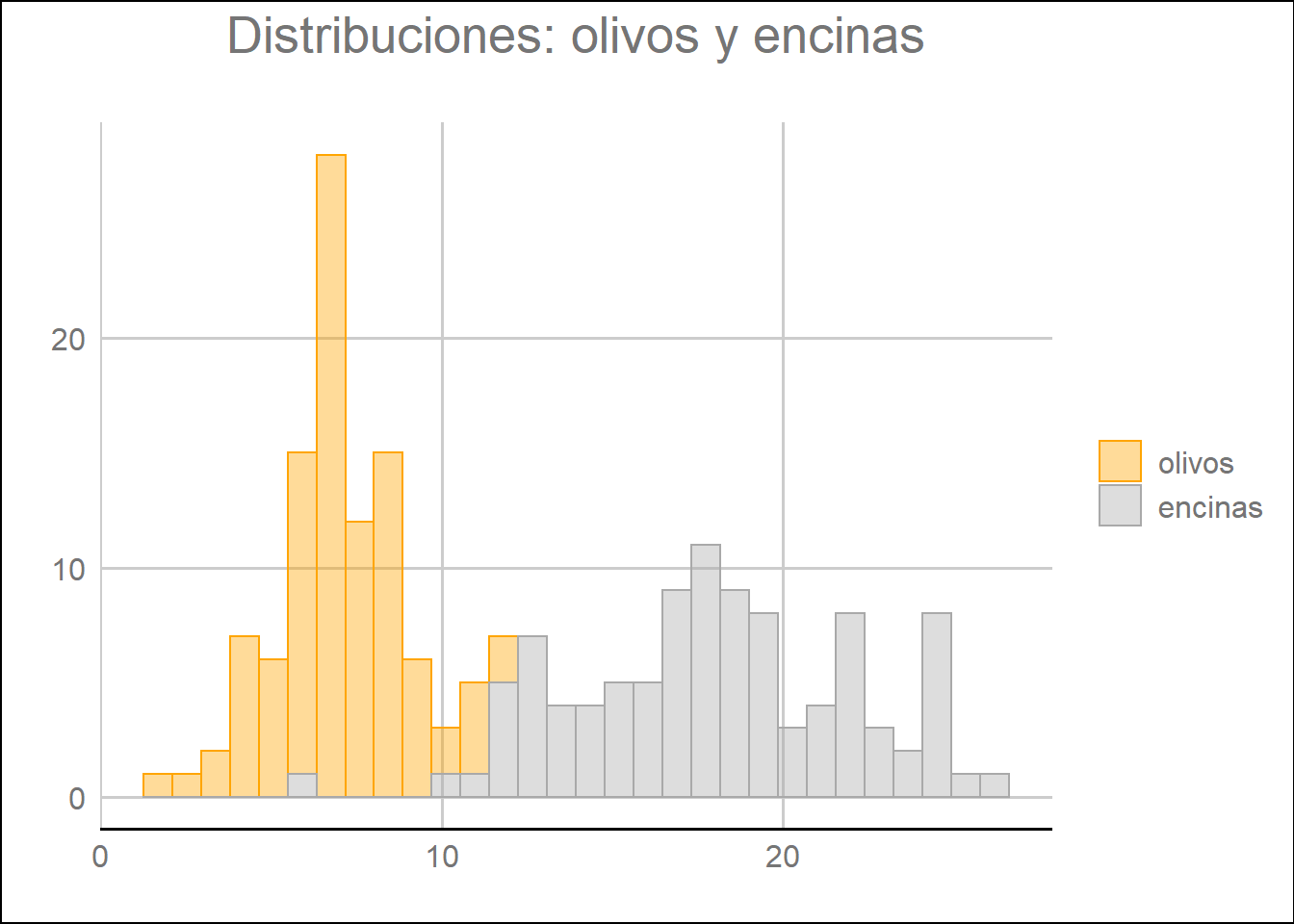
Para comprobar que los valores de las distribuciones de nuestras muestras creadas con la función rnorm() se ajusta a los valores de las distribuciones con los parámetros indicados realizamos el siguiente ejercicio: Identificamos la media y la desviación estándar para ambas muestras y graficamos sendas distribuciones en nuestro gráfico.
mean_df_olivo <- mean(df$olivo)
sd_df_olivo <- sd(df$olivo)
mean_df_encina <- mean(df$encina)
sd_df_encina <- sd(df$encina)
ggplot(df_arbol, aes(x= value, fill = variable, color = variable)) +
stat_function(fun = dnorm, n=100, args = list(mean = mean_df_olivo, sd= sd_df_olivo), col = "orange", size = 2) +
stat_function(fun = dnorm, n=100, args = list(mean = mean_df_encina, sd= sd_df_encina), col = "darkgrey", size = 2) +
geom_histogram(aes(y = ..density..), alpha = 0.2, bins = 30) +
scale_fill_manual(values = c("orange", "darkgrey")) +
scale_color_manual(values = c("orange", "darkgrey")) +
ylab("") +
labs(title = "Distribución de los olivos y las encinas",
subtitle = bquote('Olivos: ('~mu==.(mean_df_olivo)~','~sigma^{2}==.(sd_df_olivo)^{2}~'), Encinas: ('~mu==.(mean_df_encina)~','~sigma^{2}==.(sd_df_encina)^{2}~') '),
x = "",
y = "") +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))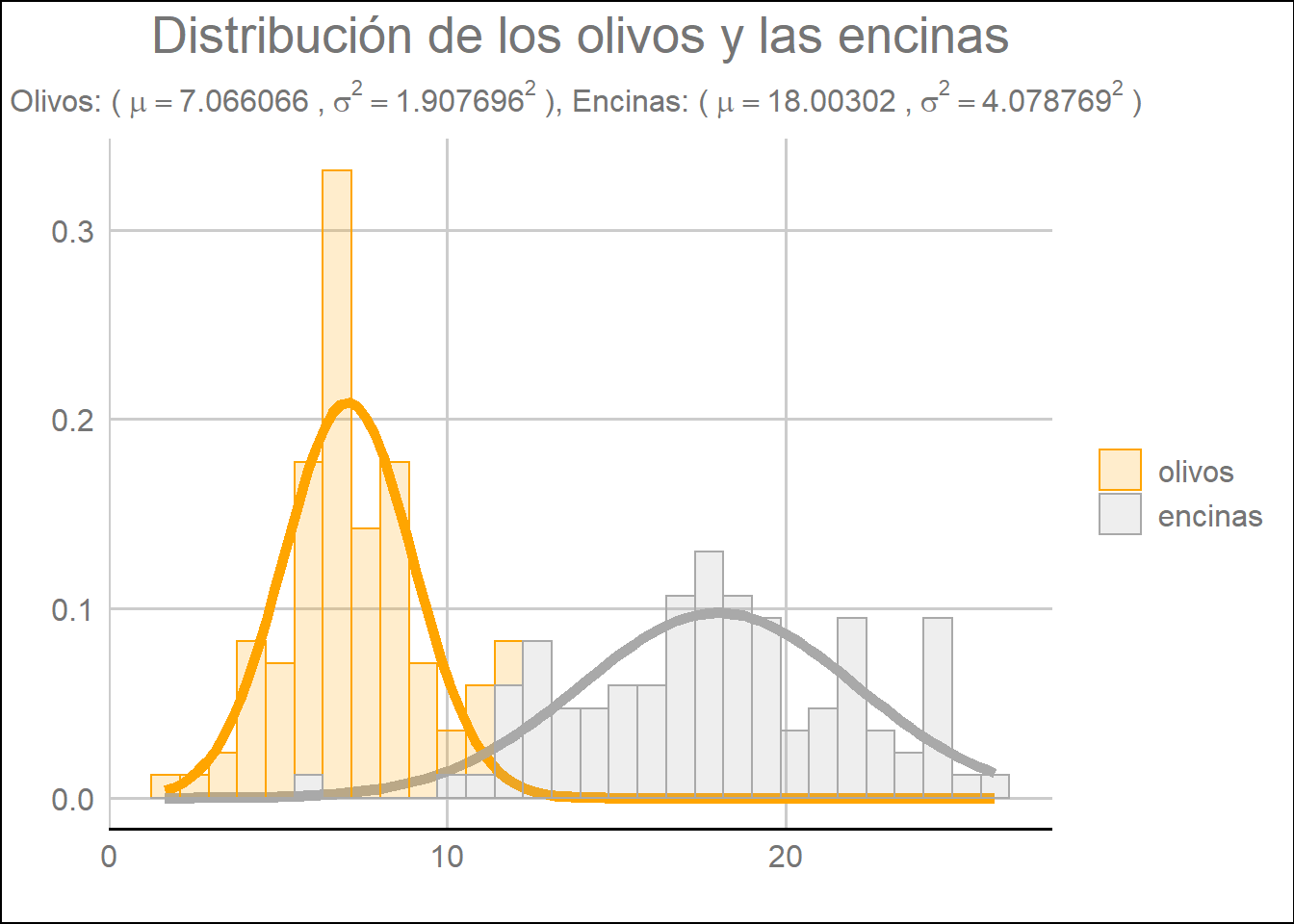
Comprobamos que las muestras aleatorias obtenidas con la función rnorm() se ajustan en gran medida a los parámetros requeridos para la distribución.
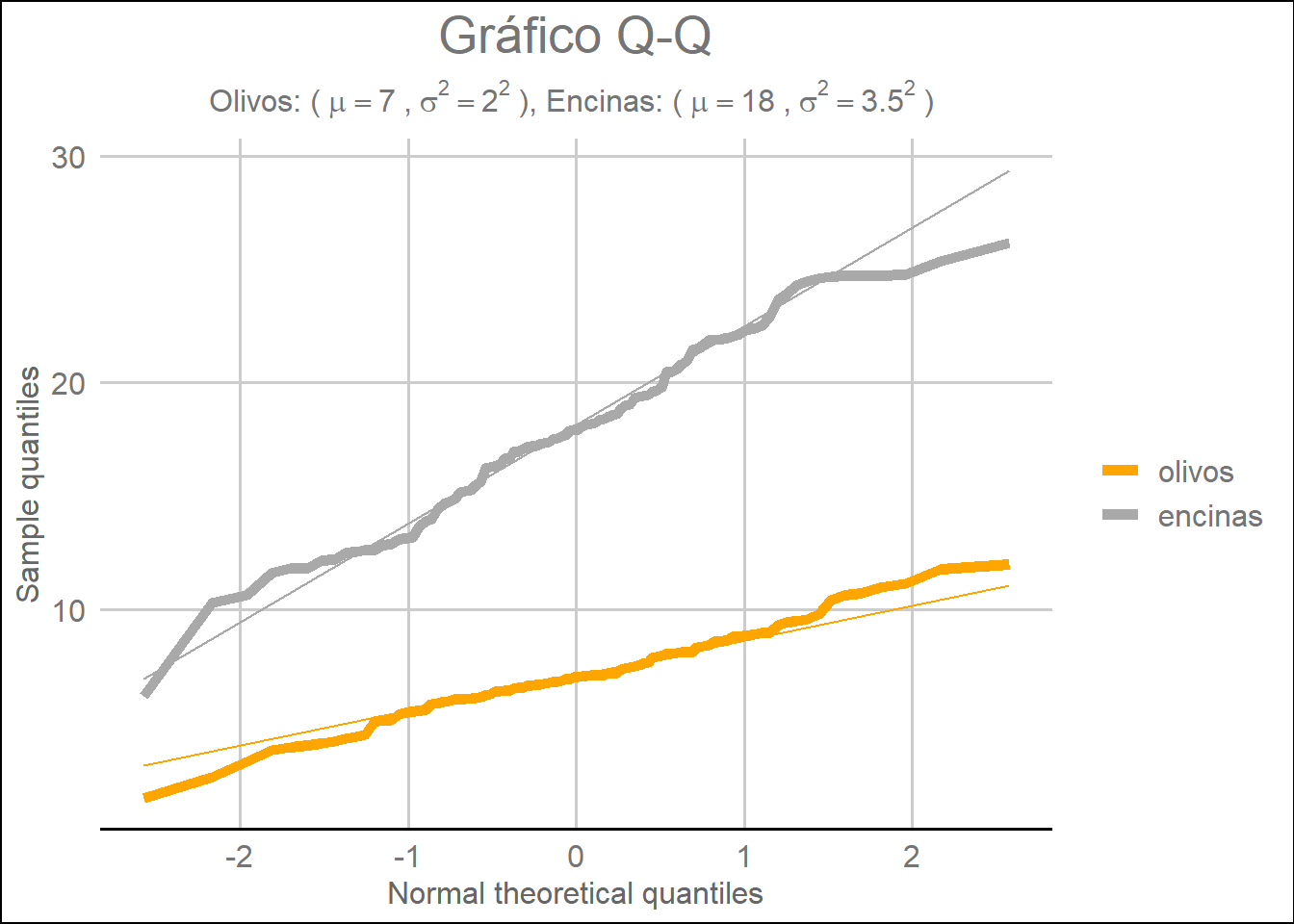
Una forma alternativa que permite determinar si la información que tenemos se corresponde con una distribución normal es el llamado gráfico Q-Q o cuantil-cuantil. Este gráfico nos permite observar cómo de cerca se encuentra nuestra distribución con respecto a una distribución normal ideal. Además, este gráfico también nos ayuda a comparar las distribuciones de diferentes conjuntos de datos. Se denomina Q-Q o cuantil-cuantil porque su mecánica consiste en comparar los cuantiles de dichas distribuciones. En nuestro caso nos interesa comparar nuestra distribución con los valores teóricos de una distribución normal estándar, por tanto, en el gráfico, debemos observar si el resultado obtenido se aproxima a una línea recta. En R existen diversas posibilidades para generar un gráfico Q-Q. Una posibilidad consiste en utilizar la función stat_qq() y/o la función stat_qq_line() de la siguiente forma:
ggplot(df_arbol) +
stat_qq(aes(sample = value, color = factor(variable))) +
stat_qq_line(aes(sample = value, color = factor(variable))) +
scale_color_manual(values = c("orange", "darkgrey")) +
ylab("") +
labs(title = "Gráfico Q-Q",
subtitle = bquote('Olivos: ('~mu==.(mean_olivo)~','~sigma^{2}==.(sd_olivo)^{2}~'), Encinas: ('~mu==.(mean_encina)~','~sigma^{2}==.(sd_encina)^{2}~') '),
x = "Normal theoretical quantiles",
y = "Sample quantiles") +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))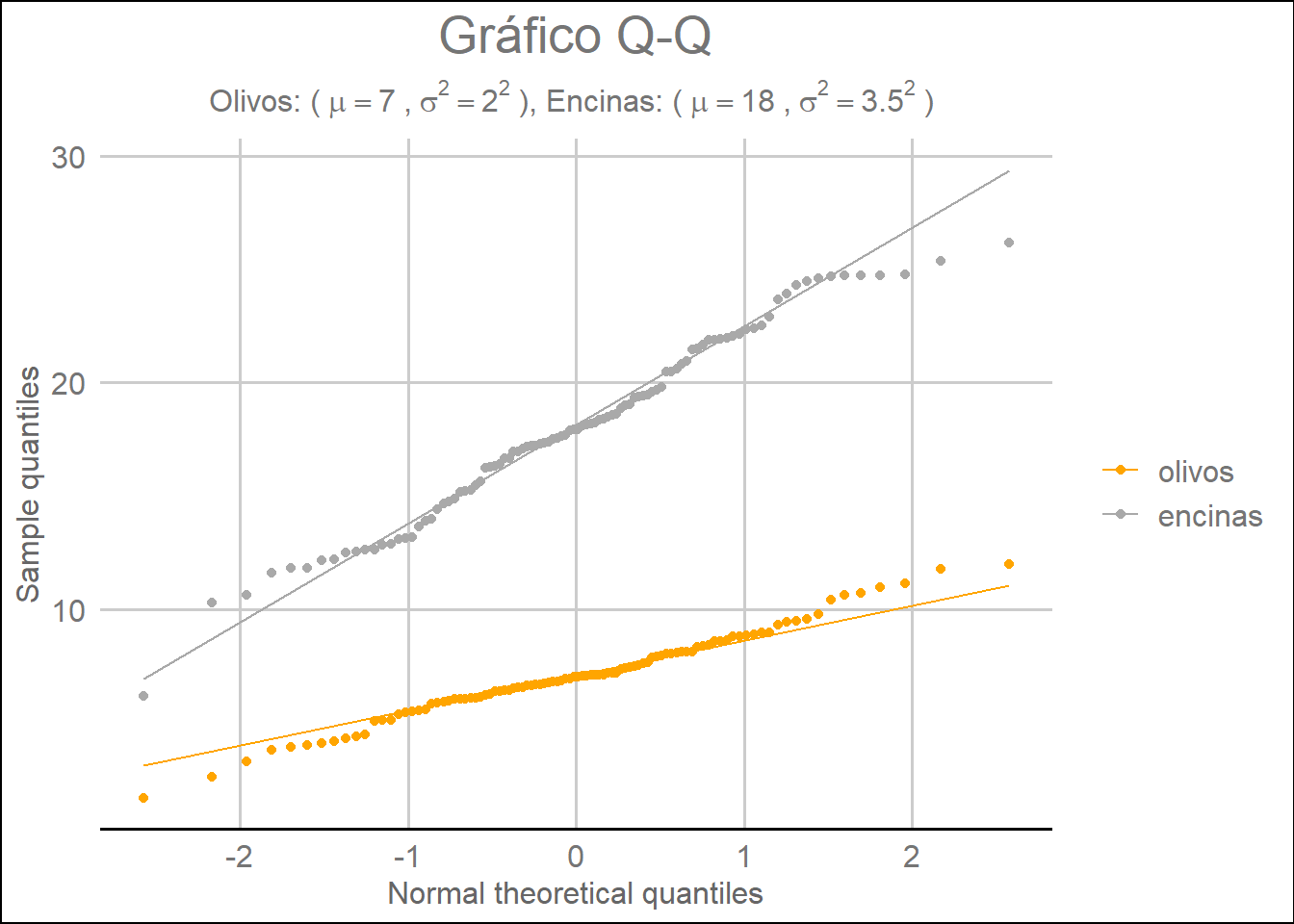
Por otra parte podemos utilizar la función geom_line(stat = "qq") y, como hacemos en nuestro caso, podemos complementar dicha función con la función stat_qq_line() utilizada en el ejemplo previo.
ggplot(df_arbol, aes(sample = value)) +
ggtitle("") +
geom_line(stat= "qq", aes(color = factor(variable)), size = 2) +
stat_qq_line(aes(sample = value, color = factor(variable))) +
scale_color_manual(values = c("orange", "darkgrey")) +
ylab("") +
labs(title = "Gráfico Q-Q",
subtitle = bquote('Olivos: ('~mu==.(mean_olivo)~','~sigma^{2}==.(sd_olivo)^{2}~'), Encinas: ('~mu==.(mean_encina)~','~sigma^{2}==.(sd_encina)^{2}~') '),
x = "Normal theoretical quantiles",
y = "Sample quantiles") +
theme_gdocs() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))