Paquetes
library(dplyr)
library(ggplot2)
library(ggthemes)
Introducción
Por lo general, el paquete {stats} de R (base R) que viene instalado por defecto incluye funciones para realizar operaciones asociadas a un gran número de distribuciones de probabilidad. La lista completa de las distribuciones incluidas en el paquete {stats} se obtiene indicando el siguiente comando: help("Distributions"), el cual nos devolverá la captura de pantalla que veremos a continuación. Se comprueba que el paquete {stats} incluye las distribuciones de probabilidad más comunes (binomial, chi-squared, exponential, F-distribution, normal distribution, etc.).
No obstante, téngase en cuenta que en CRAN podemos acceder a un gran número de paquetes donde se incluyen otras distribuciones más especializadas, u otros paquetes alternativos para trabajar con las distribuciones ya incluidas en {stats}. Una lista de dichos paquetes se puede consultar en el siguiente enlace.
En {stats} cada distribución de probabilidad tiene un nombre asignado y para cada una de ellas existen cuatro distintas funciones: función de densidad o de probabilidad (density), función de distribución (distribution function), función cuantílica (quantile function) y una función para la generación de números aleatorios (random variate generation), tal y como se explica en los detalles de la captura de pantalla mostrada previamente. Como se puede deducir de los respectivos nombres, la función density calcula la densidad (pdf) en un determinado valor, la función de distribución nos devuelve la distribución acumulada (cdf), la función cuantílica calcula el cuantil correspondiente a una determinada probabilidad y la última función genera un conjunto de valores aleatorios de una determinada distribución. Dichas funciones se indican anteponiendo los prefijos: d, p, q o r respectivamente al nombre asignado a cada distribución. Por ejemplo, para el caso de la distribución de Poisson, que trataremos en este post, las funciones serán: dpois(), ppois(), qpois() y rpois()
Señalar que entre las distribuciones incluidas en {stats} podemos diferenciar entre distribuciones discretas y distribuciones continuas, donde las primeras no asumen valores intermedios entre dos números enteros mientras que las segundas si lo hacen. Entre las primeras distribuciones discretas encontramos, por ejemplo, la distribución binomial (binom), la distribución Poisson (pois) o la geométrica (geom). Entre las continuas tenemos la distribución normal (norm), la t-Student (t) o la distribución chi-cuadrado (chisq) entre otras.
Distribución de Poisson
La distribución de Poisson es, como se ha señalado, una distribución de probabilidad discreta, al igual que la distribución binomial. La distribución de Poisson se aplica a las ocurrencias de sucesos independientes durante un intervalo determinado. La ocurrencia media por intervalo suele representarse con la letra griega lambda (\(\lambda\)) y, en base a dicho valor, la distribución de Poisson estima la probabilidad de que se produzcan x sucesos dentro de un intervalo dado. Téngase en cuenta que dicho intervalo puede ser de tiempo, pero también cabe la posibilidad que el intervalo corresponda a otro tipo de unidad como por ejemplo distancia, volumen, área o fenómenos de distinta naturaleza como podría ser el número de crías de un animal determinado.
La representación matemática de la distribución de Poisson es la siguiente:

Como ya explicamos en la distribución binomial, y tal y como sucede en todas las distribuciones de probabilidad del paquete {stats}, disponemos de cuatro funciones con las que trabajar de forma sencilla en R. En este caso la función dpois() será la probabilidad de que se produzca determinado suceso durante un determinado periodo de tiempo (teniendo en cuenta el esperado número de eventos), ppois() devolverá la probabilidad acumulada, qpois() indicará el cuantil atendiendo a una probabilidad acumulada señalada y, por último rpois() creará una lista de valores de una distribución de Poisson atendiendo a los criterios establecidos.
Supongamos que por infojobs he conseguido el puesto de Guardián del Puente de la Muerte y, como tal, mi función consistirá en plantear tres acertijos a aquellos intrépidos que desean cruzar dicho puente. (Obvia decir que si no consiguen responder dichos acertijos los viajeros deberán pagar con su vida.) Aunque el trabajo, a priori, parece interesante, me empiezo a plantear que quizá el día a día en ese trabajo puede ser un poco aburrido si debido a la mala fama del puente (o puede que incluso del guardián) los viajeros consideren que resulta más rentable dar un rodeo para cruzar el rio por algún otro sitio un poco menos demandante para su integridad física. No obstante, al plantear mi preocupación al departamento de recursos humanos me han comentado que, en función de los datos que tienen de los últimos años, el número esperado de viajeros que intentan cruzar el puente durante las horas que dura mi turno de 8 horas es 15. Lambda, por tanto, será 15.
En función de la ecuación presentada previamente, supongamos que me interesa saber la probabilidad que vayan a llegar 10 personas al puente durante una jornada de trabajo. Sustituyendo en la ecuación obtendríamos que dicha probabilidad es de:
lambda = 15
x = 10
((lambda)^x * exp(-lambda)) / factorial(x)
## [1] 0.04861075
No obstante, para dicha tarea podemos hacer uso de la función dpois(), la cual nos permite estimar de forma sencilla dichas probabilidades. Pongamos que queremos saber la probabilidad de que lleguen menos o más viajeros a lo largo de mi jornada de trabajo. Veamos por ejemplo cuál sería la probabilidad de que 0, 5, 10, 15 y 20 intrepidos viajeros quieran cruzar el puente.
lam = 15
dpois(0, lam)
## [1] 0.0000003059023
dpois(5, lam)
## [1] 0.001935788
dpois(10, lam)
## [1] 0.04861075
dpois(15, lam)
## [1] 0.1024359
dpois(20, lam)
## [1] 0.04181031
Con una pequeña modificación del código previo podemos también estimar cada probabilidad relativa a la llegada de 0 a 20 viajeros.
x <- 0:20
y <- dpois(0:20, lambda = 15)
data.frame("Prob"=y,row.names=x)
## Prob
## 0 0.0000003059023
## 1 0.0000045885348
## 2 0.0000344140111
## 3 0.0001720700553
## 4 0.0006452627073
## 5 0.0019357881219
## 6 0.0048394703048
## 7 0.0103702935103
## 8 0.0194443003318
## 9 0.0324071672197
## 10 0.0486107508296
## 11 0.0662873874949
## 12 0.0828592343686
## 13 0.0956068088869
## 14 0.1024358666645
## 15 0.1024358666645
## 16 0.0960336249980
## 17 0.0847355514688
## 18 0.0706129595574
## 19 0.0557470733348
## 20 0.0418103050011
La distribución de probabilidad se puede representar gráficamente de la siguiente forma:
data.frame(llegadas = 0:25, p = dpois(x = 0:25, lambda = 15)) %>%
ggplot(aes(x = factor(llegadas), y = p, fill= "orange")) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 2,
vjust = 0) +
labs(title = "Probabilidad de llegada de visitantes",
subtitle = "(lambda = 15)",
x = "Número de posibles visitantes",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 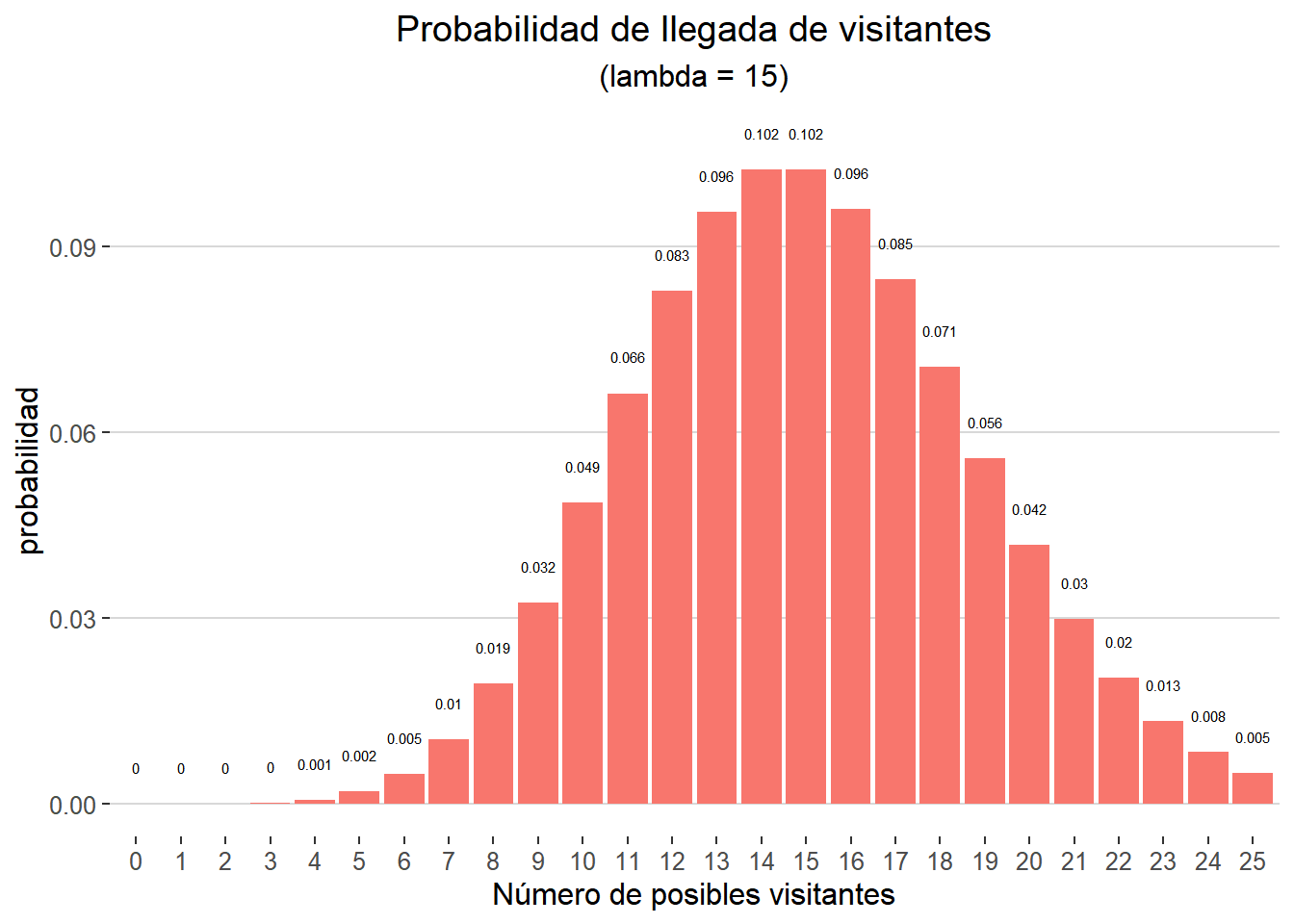
Al llegar al puente en mi primer día de trabajo me encuentro a un compañero, otro guardián del puente, que justo termina su jornada laboral. Hablando con él de acertijos, viajeros intrepidos y muertes dolorosas sale a colación el tema que me preocupaba. Parece ser que no es cierto que la media de visitantes durante mi jornada sea de 15 personas como aseguran en recursos humanos. Según el guardián debería esperar aproximadamente la llegada de cinco personas. Menuda diferencia! Entonces, si calculo de nuevo las probabilidades de llegada de visitantes de acuerdo a la nueva información podría generar el siguiente gráfico:
data.frame(llegadas = 0:25, p = dpois(x = 0:25, lambda = 5)) %>%
ggplot(aes(x = factor(llegadas), y = p, fill= "orange")) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 2,
vjust = 0) +
labs(title = "Probabilidad de llegada de visitantes",
subtitle = "(lambda = 5)",
x = "Número de posibles visitantes",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) 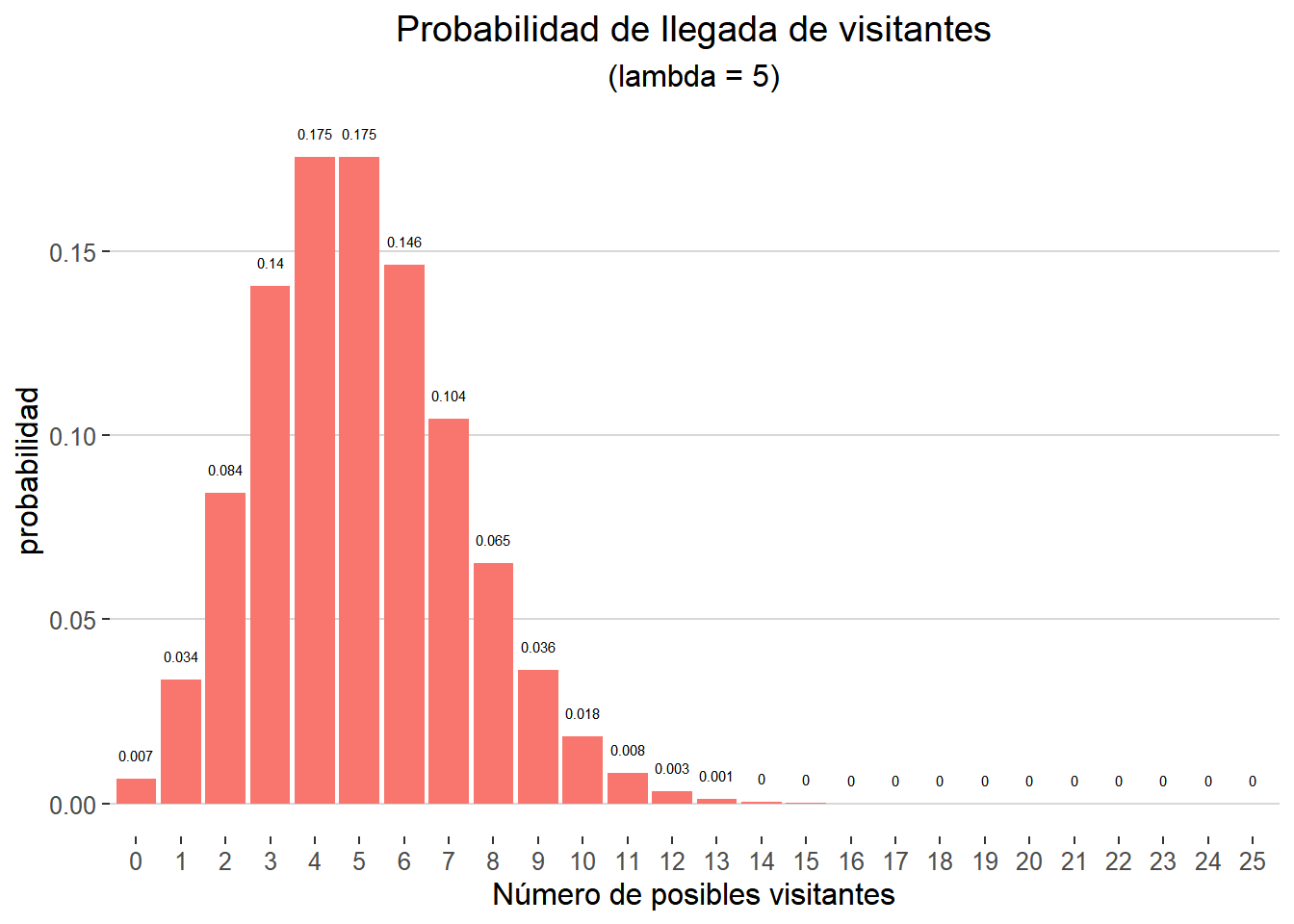
Todo parece indicar que la jornada se me va a hacer bastante lenta.
Una vez me aceptada la realidad de mi nuevo empleo no puedo evitar hacerme nuevas preguntas. La primera de ellas: ¿Qué probabilidad habrá, teniendo en cuenta la información que me ofrece el guardián, de que reciba 5 o menos visitas durante mi jornada? Para ello no me sirve conocer una probabilidad de visitas determinada sino que necesito calcular la probabilidad acumulada. Como indicamos previamente, la función ppois() nos permite obtener dicha probabilidad de forma sencilla.
ppois(q = 5, lambda = 5, lower.tail = TRUE)
## [1] 0.6159607
Gráficamente podemos representar la probabilidad acumulada (de 0 a 5 visitantes) de la siguiente forma:
data.frame(llegadas = 0:15, p = ppois(q = 0:15, lambda = 5, lower.tail = TRUE)) %>%
mutate(result = ifelse(llegadas <= 5, "si", "no")) %>%
ggplot(aes(x = factor(llegadas), y = p,fill = result)) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 3,
vjust = 0) +
labs(title = "Probabilidad acumulada de llegada de visitantes(<= 5)",
subtitle = "(lambda = 5)",
x = "Número de posibles visitantes",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))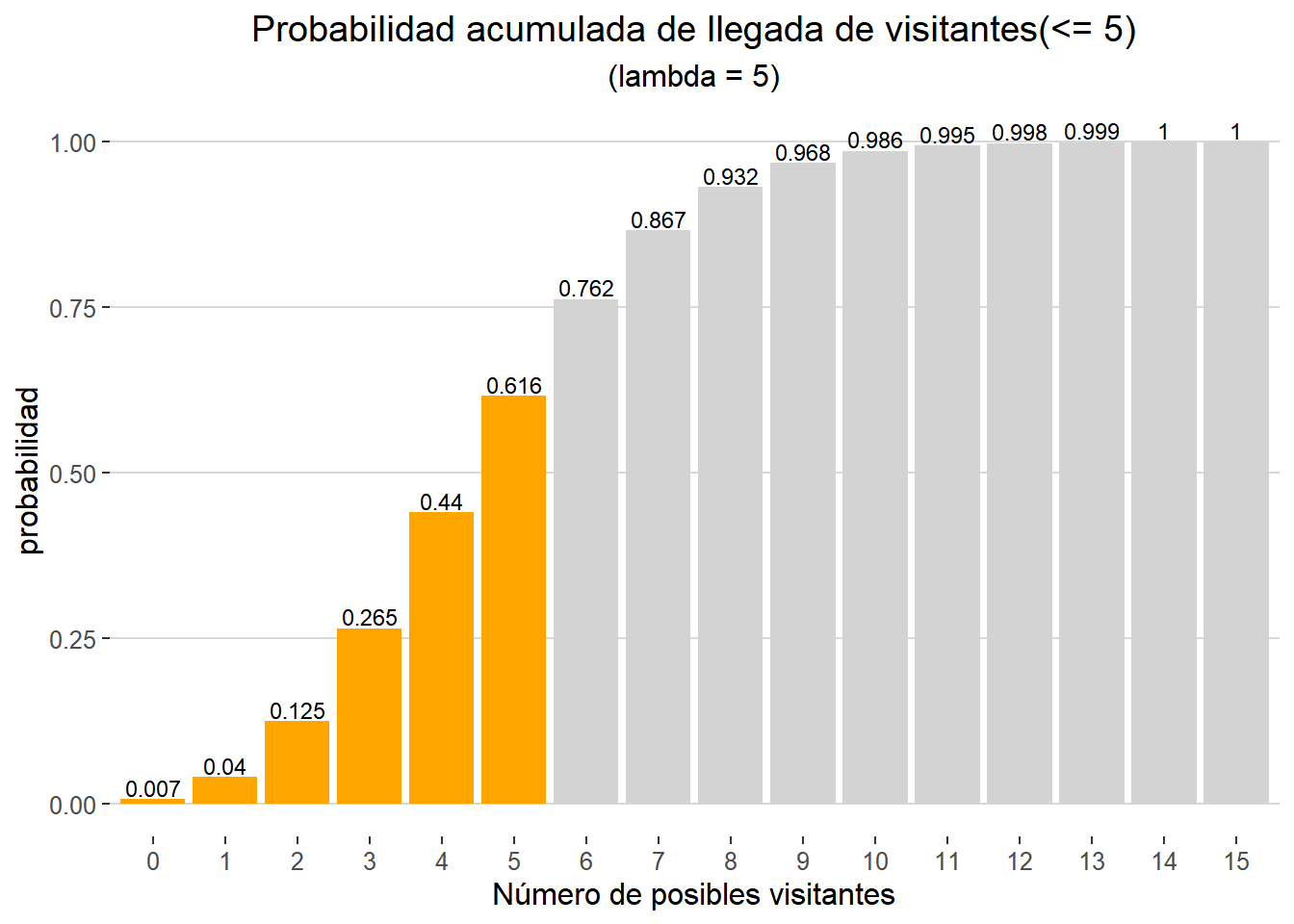
Si, por el contrario, me interesa saber la probabilidad acumulada de recibir seis o más visitantes durante mi primer día de trabajo utilizaríamos el siguiente código (indicando lower.tail = FALSE).
ppois(q = 5, lambda = 5, lower.tail = FALSE)
## [1] 0.3840393
Con unas pequeñas modificaciones al código previo podemos representar la nueva probabilidad acumulada de la siguiente forma:
data.frame(llegadas = 0:15, p = ppois(q = -1:14, lambda = 5, lower.tail = FALSE)) %>%
mutate(result = ifelse(llegadas >= 6, "si", "no")) %>%
ggplot(aes(x = factor(llegadas), y = p,fill = result)) +
geom_col() +
geom_text(aes(label = round(p,3), y = p + 0.005),
size = 3,
vjust = 0) +
labs(title = "Probabilidad acumulada de llegada de visitantes (>=6)",
subtitle = "(lambda = 5)",
x = "Número de posibles visitantes",
y = "probabilidad") +
guides(fill = FALSE) +
theme_hc() +
theme(legend.title = element_blank(),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)) +
scale_fill_manual(values = c("si" = "orange", "no" = "lightgrey"))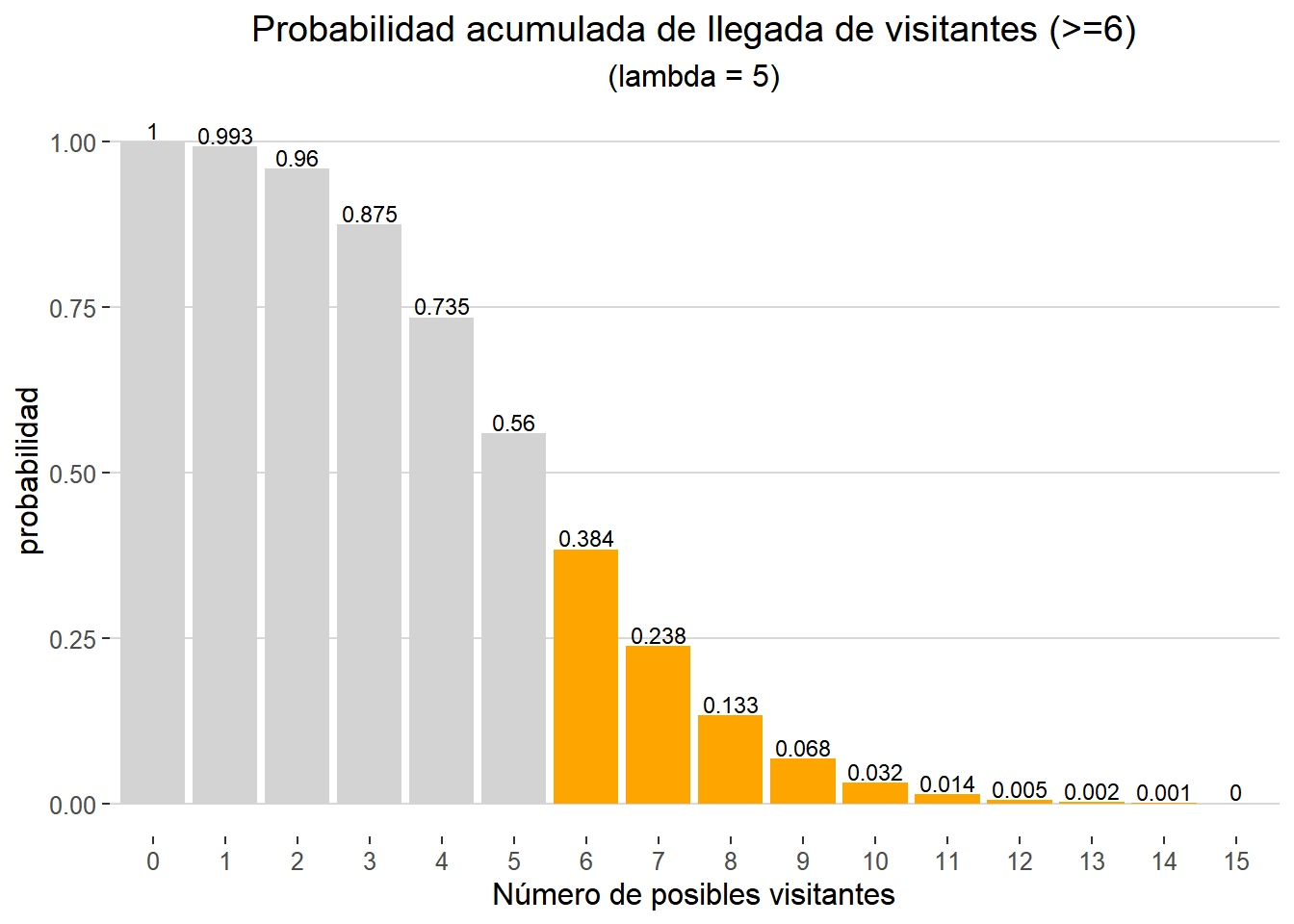
La función ’qpois()` nos indica los cuantiles de la distribución. Por ejemplo, supongamos que queremos saber los cuantiles 10, 40, 60 y 80 de la distribución (lambda = 5)
qpois(0.1, 5)
## [1] 2
qpois(0.4, 5)
## [1] 4
qpois(0.6, 5)
## [1] 5
qpois(0.8, 5)
## [1] 7
Para obtener todos los cuantiles de la distribución podríamos formular el siguiente código:
qpois(seq(0.1, 0.9, 0.1), 5)
## [1] 2 3 4 4 5 5 6 7 8