Librerías / Paquetes
library(tidyverse)
library(ggplot2)
library(mFilter)
library(readxl)
library(DT)
library(ggfortify)
library(zoo)
library(gridExtra)
library(reshape)
library(plotly)
library(RColorBrewer)
library(corrplot)
#theme:
source("https://github.com/traffordDataLab/assets/raw/master/theme/ggplot2/theme_lab.R")
Introducción
A pesar de sus limitaciones y sus críticas (ver, por ejemplo, el artículo de James D. Hamilton publicado en Review of Economics and Statistics) el filtro de Hodrick- Prescott (HP) continúa siendo una herramienta muy popular y extensamente utilizada para extraer de una serie temporal sus componentes de tendencia y ciclo. Este filtro fue propuesto en 1980 por Robert J. Hodrick y Edward C. Prescott y su formulación deriva de lo siguiente:

Aplicación a nivel nacional
Para ejemplificar la aplicación del filtro HP en R vamos en primer lugar a utilizar la serie del valor agregado bruto por habitante en Perú entre 1995 y 2016. Posteriormente realizaremos una pequeña comparativa con el resto de las regiones (departamentos) del país.
Para ello descargamos los datos con información referente al VAB por habitante en cada región del país así como el VAB por habitante del conjunto de la nación peruana para el periodo señalado. Los valores están en soles constantes de 2007 y son obtenidos partiendo de información del Instituto Nacional de Estadística e Informática del Perú. La estructura de los datos es la siguiente:
df_HP <- read_excel("C:/Users/Usuario/Desktop/r_que_r/r_que_r/content/datasets/1995_2016_VABPC_de07_con_T_NACIONAL.xlsx")
df_HP
## # A tibble: 25 x 26
## Region Name id Geo `1995` `1996` `1997` `1998` `1999` `2000` `2001`
## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Amazo~ Amaz~ AMA Selva 2932 3234 3184 3358 3212 3251 3202
## 2 Áncash Anca~ ANC Costa 8358 8879 8702 7982 9520 9610 10664
## 3 Apurí~ Apur~ APU Sier~ 3393 3553 3638 3407 3611 3514 3058
## 4 Arequ~ Areq~ ARE Costa 9310 9277 9792 9615 9594 9764 9956
## 5 Ayacu~ Ayac~ AYA Sier~ 3194 3257 3416 3466 3490 3507 3466
## 6 Cajam~ Caja~ CAJ Sier~ 3708 3738 4150 4505 4762 4913 4810
## 7 Cusco Cusco CUS Sier~ 5698 5690 6052 6045 5851 5901 5748
## 8 Huanc~ Huan~ HUAV Sier~ 4785 5076 5386 5404 5406 5136 4966
## 9 Huánu~ Huan~ HUAC Sier~ 3424 3541 3680 3538 3545 3598 3439
## 10 Ica Ica ICA Costa 8551 8313 8864 8183 8336 8522 8194
## # ... with 15 more rows, and 15 more variables: `2002` <dbl>, `2003` <dbl>,
## # `2004` <dbl>, `2005` <dbl>, `2006` <dbl>, `2007` <dbl>, `2008` <dbl>,
## # `2009` <dbl>, `2010` <dbl>, `2011` <dbl>, `2012` <dbl>, `2013` <dbl>,
## # `2014` <dbl>, `2015` <dbl>, `2016` <dbl>
Evolución del VAB por habitante
Antes de aplicar el filtro HP, observemos como ha sido la evolución del VAB por habitante a nivel nacional en el periodo de estudio. Para ello realizaremos unas pequeñas modificaciones al dataset anterior, seleccionando únicamente los valores para el conjunto del país y transformamos la estructura del dataframe a un formato largo con la función gather(). A continuación realizamos nuestro gráfico con {ggplot2} aplicando algunas modificaciones de estilo.
# DATASET PARA PERU (NACIONAL)
df_total <- df_HP %>%
filter(Name == "PERU") %>%
gather(key = year, value = vabpc, 5:26) %>%
select(Name, year,vabpc) %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
# LINEPLOT DEL VABPC
ggplot(df_total, aes(x= year, y= vabpc)) +
geom_line(colour = "orange", size = 1) +
geom_point(colour = "darkgrey", size = 2) +
scale_x_date(breaks = df_total$year, date_labels = "%Y") +
scale_y_continuous(labels = scales::comma) +
labs(title= "Valor Agregado Bruto per cápita . \n(Perú. 1995-2016)",
subtitle="(Valores constantes de 2007)",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))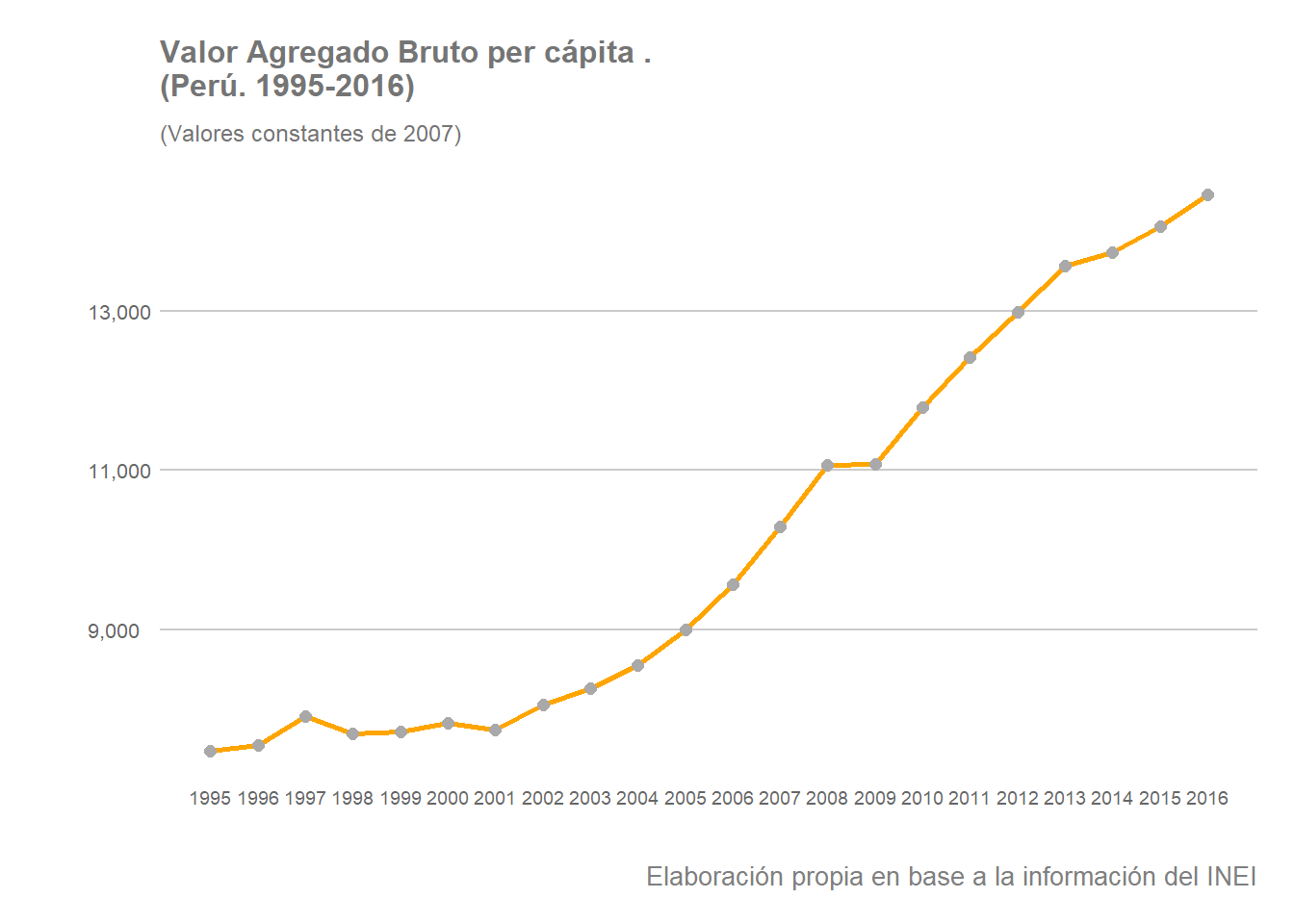
La tendencia del valor agregado bruto por habitante en el Perú es claramente ascendente, especialmente desde el año 2001, con un pequeño bache en 2008-2009, fruto de la crisis financiera internacional.
Tasas de crecimiento anual del VABpc
En segundo lugar veamos cómo son las tasa de crecimiento anual de esta variable durante nuestro periodo de análisis:
# ESTIMAMOS LA TASA DE CRECIMIENTO Y CONVERTIMOS EN TIMESERIE
peru_log <- log(df_total[,3])
peru_tasa <- diff(peru_log$vabpc)
peru_tasa_ts<- ts(peru_tasa, frequency=1,start=1996)
# NOTA: Para representar gráficamente la serie temporal obtenida podríamos utilizar la función autoplot del paquete {ggfortify} de la siguiente forma:
# autoplot(peru_tasa_ts, colour ="orange", size = 1) + theme_lab()
# Sin embargo, para poder utilizar ggplot2 con un ts debemos transformar la informar a un dataframe. La operación será la siguiente:
df_P <- data.frame(date=as.Date(as.yearqtr(time(peru_tasa_ts))),
tasa_p = as.matrix(peru_tasa_ts))
# LINEPLOT DE LAS TASAS DE CRECIMIENTO ANUALES DEL VABPC:
ggplot(data=df_P, mapping=aes(x=date, y=tasa_p)) +
geom_hline(aes(yintercept = 0),colour="darkblue", size = 1.5) +
geom_line(colour = "orange", size = 1) +
geom_point(colour = "darkgrey", size = 2) +
scale_x_date(breaks = df_total$year, date_labels = "%Y") +
scale_y_continuous(labels = scales::comma) +
labs(title= "Valor Agregado Bruto per cápita . \n(Perú. 1995-2016)",
subtitle="(Tasa de crecimiento anual)",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))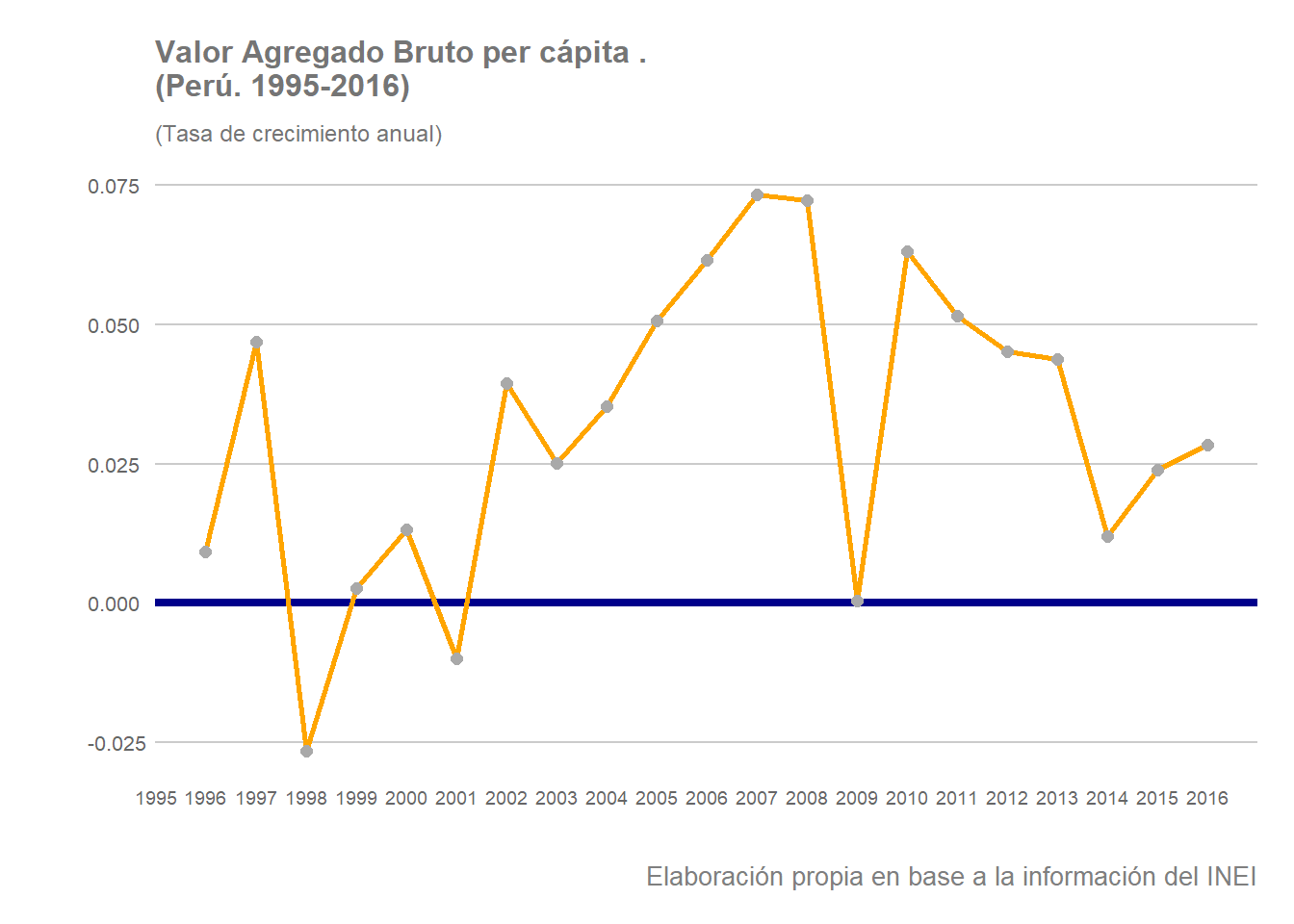
Se observa que tras unos años de mayor inestabilidad, a partir de los años 2002-2003 Perú inicia un periodo de crecimiento sostenido, a excepción del año 2009 cuando sufre una fuerte reducción en su tasa de crecimiento llegando a registrar ese año un crecimiento prácticament nulo. El periodo que se inicia al principio de la década pasada se denominó popularmente como milagro peruano y generó un gran optimismo con respecto al futuro del país tanto entre la población como entre muchos analistas e investigadores sociales. No obstante, el crecimiento del VABpc en los últimos años ha empezado a mostrar una tendencia decreciente generando con ello una mayor incertidumbre con respecto al porvenir del país. Esta sensación se ha visto empeorada recientemente como resultado del fenómeno del niño que arrasó gran parte del litoral del país, especialmente en el norte, entre 2016 y 2017 y de la pandemia que estamos viviendo globalmente en la actualidad.
Filtro Hodrick-Prescott
Una vez hemos observado la evolución del VAB per cápita y las tasas de variación anual procederemos a calcular el filtro Hodrick-Prescott. La forma sencilla de calcular y representar gráficamente el componente tendencial y el cíclico es utilizando la función hpfilter() del paquete {mFilter} y, posteriormente, realizar el gráfico con la función plot(). Esta operación se realiza con unas pocas líneas de código y el resultado sería el siguiente:
lambda_hp <- 100
peru.hp <- hpfilter(peru_log, type="lambda", freq=lambda_hp)
plot(peru.hp, ask= FALSE)
abline(h=0, col="orange")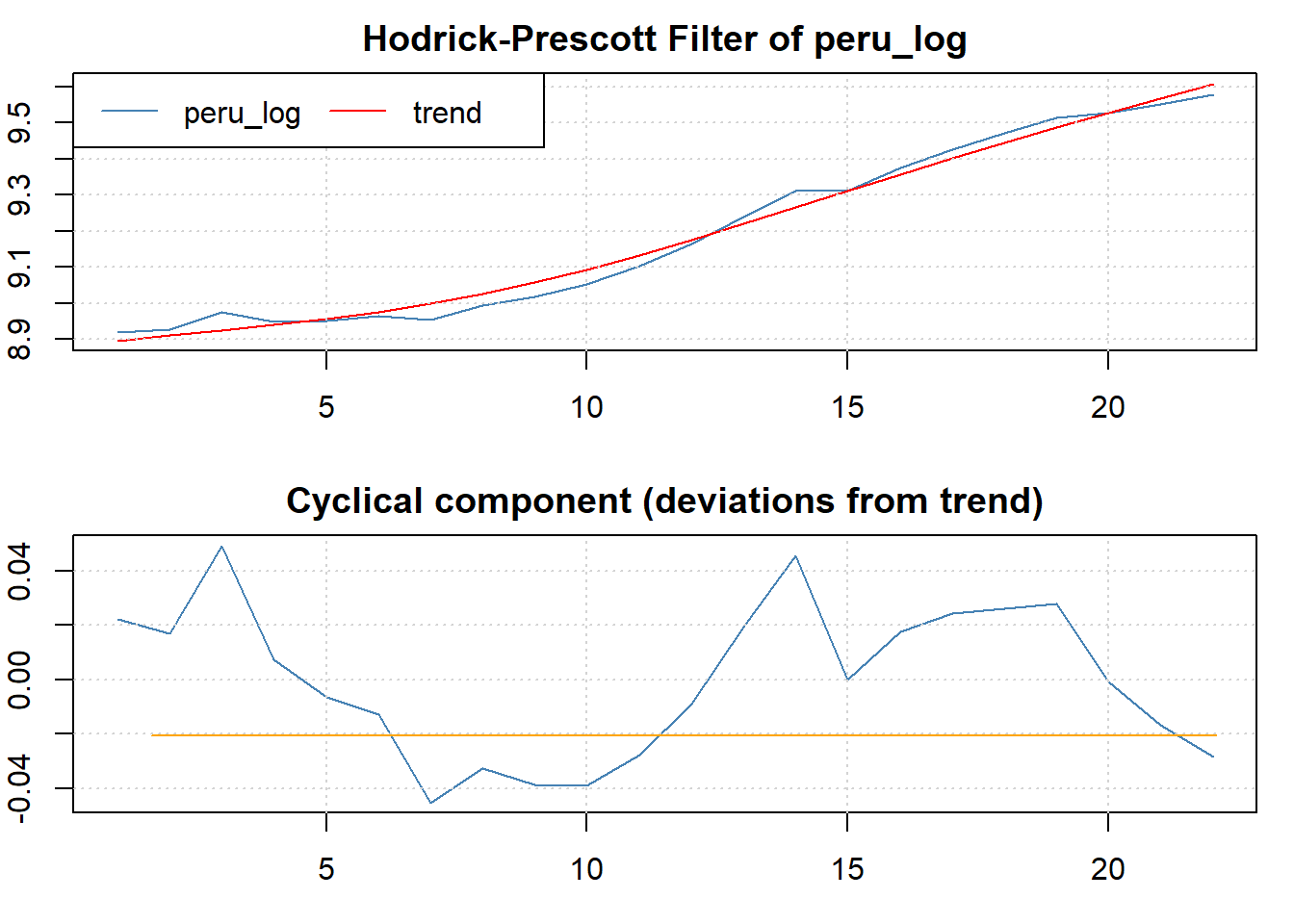
No obstante, si queremos representar los componentes del filtro HP con {ggplot2} y, de esta forma, customizar el gráfico a nuestro gusto, debemos realizar una serie de operaciones en tanto que debemos transformar los datos a un formato dataframe. Una posibilidad para llevar a cabo dichas operaciones sería la siguiente:
# VER: https://stackoverflow.com/questions/39870163/transform-mfilter-object-list-of-time-series-to-plot-with-ggplot2
# LOS NOMBRES DE LAS VARIABLES OBTENIDAS SERÍAN LOS SIGUIENTES.
names(peru.hp)
## [1] "cycle" "trend" "fmatrix" "title" "xname" "call" "type"
## [8] "lambda" "method" "x"
lista = list(peru.hp$x, peru.hp$trend, peru.hp$cycle)
names(lista) = c("vabpc", "trend", "cycle")
sapply(lista, class)
## vabpc trend cycle
## "matrix" "matrix" "numeric"
# TRANSFORMAMOS A DATAFRAME:
fn_ts_to_DF = function(x) {
DF = data.frame(date=zoo::as.Date(time(lista[[x]])),tseries=as.matrix(lista[[x]]))
colnames(DF)[2]=names(lista)[x]
return(DF)
}
DFList=lapply(seq_along(lista),fn_ts_to_DF)
names(DFList) <- c("vabpc","trend","cycle")
seriesTrend <- merge(DFList$vabpc, DFList$trend, by="date")
cycleSeries <- DFList$cycle
seriesTrend <- seriesTrend %>%
mutate(date = c(1995:2016)) %>%
mutate(date = as.Date(paste(date, "-01-01", sep = "", format='%Y-%b-%d')))
cycleSeries <- cycleSeries %>%
mutate(date = c(1995:2016)) %>%
mutate(date = as.Date(paste(date, "-01-01", sep = "", format='%Y-%b-%d')))
Una vez tenemos nuestro dataframe podemos utilizar la operativa habitual del paquete {ggplot2}. Realizamos dos gráficos, en el primero mostraremos la evolución en logaritmos del VAB por habitante y el componente tendencial y en el segundo el componente cíclico. Uniremos ambos gráficos con la función grid.arrange() del paquete {gridExtra}.
gSeries <- ggplot(melt(seriesTrend, "date"),
aes(x=date,y=value, color=variable)) +
geom_line() +
scale_color_manual(values = c("darkgrey", "orange")) +
labs(title= "Filtro Hodrick-Prescott para el VAB por habitante. \n(Perú. 1995-2016)",
subtitle="Componente tendencial",
x= NULL,
y="") +
scale_x_date(breaks = seriesTrend$date, date_labels = "%Y") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 6),
axis.text.x=element_text(colour="grey40",
size = 5),
plot.title=element_text(size = 9,
hjust = 0),
plot.subtitle = element_text(size = 8,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.title = element_blank(),
legend.text = element_text(color = "grey40", size = 8, hjust = 0))
gCycle <- ggplot(cycleSeries,aes(x=date,y=cycle)) +
geom_hline(aes(yintercept = 0),colour="darkblue", size = 1.2) +
geom_line(color="orange") +
labs(title= "Componente cíclico (Desviación de la tendencia)",
subtitle="",
x= NULL,
y="") +
scale_x_date(breaks = seriesTrend$date, date_labels = "%Y") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 6),
axis.text.x=element_text(colour="grey40",
size = 5),
plot.title=element_text(size = 9,
hjust = 0),
plot.subtitle = element_text(size = 8,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))
gComb = grid.arrange(gSeries,gCycle, nrow=2)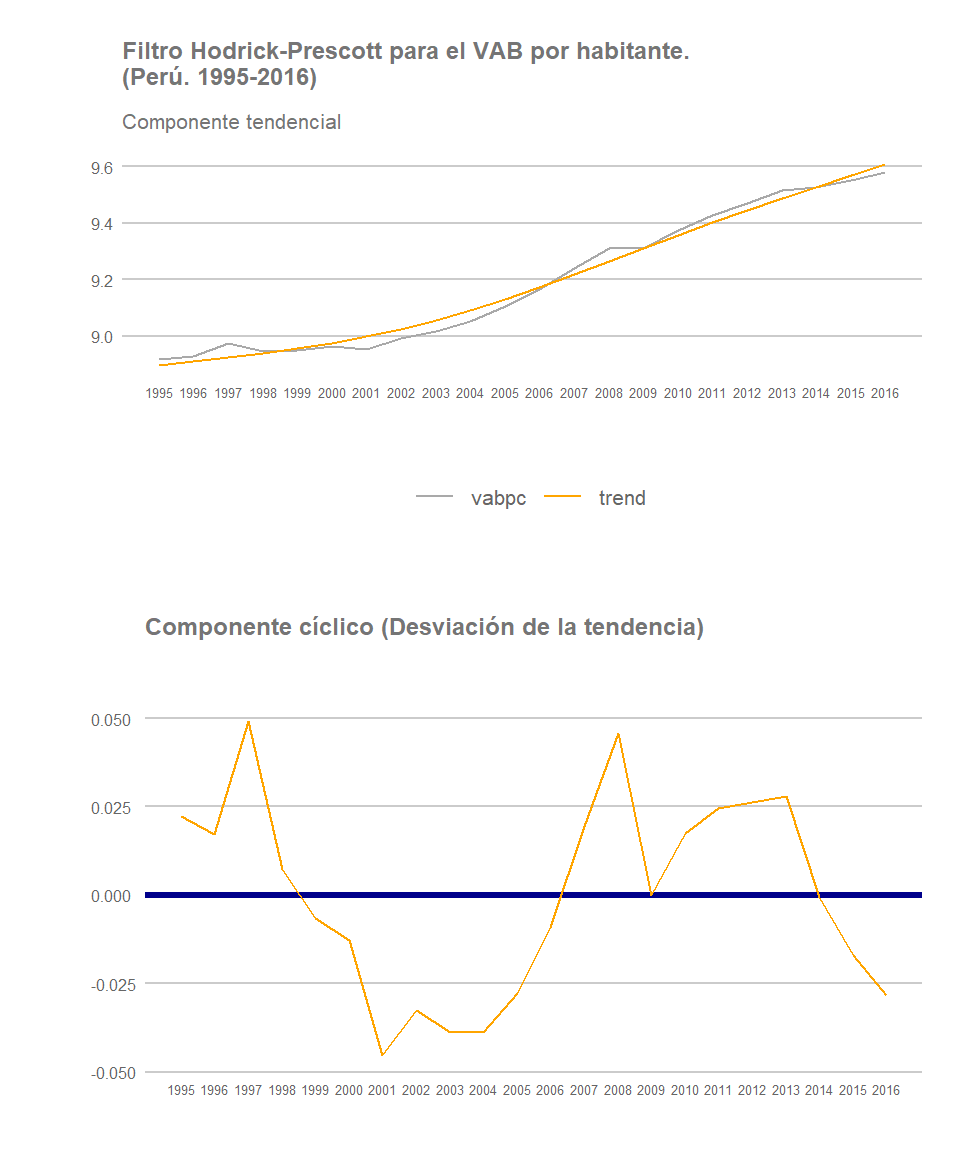
Comparativa a nivel regional
En el apartado previo hemos visto cómo aplicar el filtro Hodrick-Prescott a una serie temporal, en nuestro caso el valor agregado bruto por habitante en Perú entre 1995 y 2016. Hemos descompuesto dicha serie en su componente tendencial y cíclico utilizando el paquete {mFilter}. Este segundo apartado pretende llevar a cabo una comparación a nivel regional utilizando una metodología similar a la anterior, es decir, identificando los componentes de tendencia y ciclo de la evolución del VAB por habitante de cada región con el objetivo de comparar estos resultados con los obtenidos a nivel nacional.
Evolución del VAB por habitante
Al igual que hicimos previamente veamos en primer lugar la evolución del VAB por habitante de cada región. En esta ocasión utilizaremos el paquete {plotly} para, de esta forma, poder identificar cuál de las líneas corresponde a cada región al pasar el cursor por encima de cualquiera de ellas. La línea naranja representará la evolución del VAB por habitante del país en su conjunto.
df_regions <- df_HP %>%
gather(key = year, value = vabpc, 5:26) %>%
select(Name, id, Geo, year, vabpc) %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
ggplotly(
df_regions %>%
ggplot() +
geom_line(data = . %>% filter(Name != "PERU"), aes(year, vabpc, group = Name),
size = 0.5, alpha = 0.5, col = "grey") +
geom_line(data = . %>% filter(Name == "PERU"), aes(year, vabpc),
size = 1.5, col = "orange") +
scale_x_date(breaks = df_total$year, date_labels = "%Y") +
scale_y_continuous(trans = 'log10',labels = scales::comma) +
labs(title= "Valor Agregado Bruto per cápita (Valores constantes de 2007) . \n(Perú regiones. 1995-2016)",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="VAB per cápita (log)") +
theme_lab() +
theme(
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))
)
## Warning: `group_by_()` is deprecated as of dplyr 0.7.0.
## Please use `group_by()` instead.
## See vignette('programming') for more help
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.
Moquegua se diferencia notablemente del resto de regiones en términos de VAB por habitante, mientras que el resto de departamentos evolucionan más cercanos al promedio nacional. Se observa un crecimiento singular del VABpc de Apurímac en el último año del periodo, pasando de situarse en el puesto más bajo del ranking regional a registrar un VABpc cercano al promedio nacional.
Tasas de variación anual del VABpc
En segundo lugar comparemos las tasas de crecimiento anual del VAB por habitante con respecto al VAB pc del país. Como se podía extraer del gráfico anterior destaca el fuerte crecimiento del VABpc en la región de Apurímac en el año 2016. Este comportamiento inusual en 2016 con respecto a su evolución anterior es debido especialmente a la fuerte expansión de la actividad extractiva que ha tenido lugar en este territorio en los últimos años. De hecho, en 2016 el porcentaje de la actividad extractiva en Apurímac llegó a representar más del 60% del VAB total en dicha región (Ver este link).
df_HP_b <- df_HP %>%
select(-(Name:Geo)) %>%
gather(key = year, value = vabpc, 2:23) %>%
spread(key = Region, value = vabpc)
logs <- apply(df_HP_b[, 2:26], 2, log)
logs <- data.frame(logs)
tasas <- apply(logs[, 1:22], 2, diff)
tasas <- data.frame(tasas)
tasas_crec <- tasas %>%
mutate(year = c(1996:2016))
names(tasas_crec)
## [1] "Amazonas" "Áncash" "Apurímac" "Arequipa"
## [5] "Ayacucho" "Cajamarca" "Cusco" "Huancavelica"
## [9] "Huánuco" "Ica" "Junín" "La.Libertad"
## [13] "Lambayeque" "Lima" "Loreto" "Madre.de.Dios"
## [17] "Moquegua" "Pasco" "PERU" "Piura"
## [21] "Puno" "San.Martín" "year"
tasas_crec<- tasas_crec[, c(23, 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,20,21,22,19)]
tasas_crecim <- tasas_crec %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d'))) %>%
gather(key = Region, value = tasa, 2:23)
ggplotly(
tasas_crecim %>%
ggplot() +
geom_line(data = . %>% filter(Region != "PERU"), aes(year, tasa, group = Region),
size = 0.5, alpha = 0.5, col = "grey") +
geom_line(data = . %>% filter(Region == "PERU"), aes(year, tasa),
size = 1.5, col = "orange") +
scale_x_date(breaks = tasas_crecim$year, date_labels = "%Y") +
#scale_y_continuous(labels = scales::comma) +
labs(title= "Tasas de crecimiento anual del VAB pc . \n(Perú Regiones. 1995-2016)",
x= NULL,
y="") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))
)
Si eliminamos el año 2016 del gráfico anterior obtenemos una imagen más nítida del comportamiento de las regiones en los años previos. Sin embargo, a pesar de la operación realizada comprobamos que resulta difícil identificar un patrón de comportamiento de características similares para el conjunto de regiones, o identificar aquellos patrones de crecimiento que se asemejan al patrón nacional.
tasas_crecim_b <- tasas_crecim %>%
filter(year != as.Date("2016-01-01"))
ggplotly(
tasas_crecim_b %>%
ggplot() +
geom_line(data = . %>% filter(Region != "PERU"), aes(year, tasa, group = Region),
size = 0.5, alpha = 0.5, col = "grey") +
geom_line(data = . %>% filter(Region == "PERU"), aes(year, tasa),
size = 1.5, col = "orange") +
scale_x_date(breaks = tasas_crecim$year, date_labels = "%Y") +
#scale_y_continuous(labels = scales::comma) +
labs(title= "Tasas de crecimiento anual del VAB pc . \n(Perú Regiones. 1995-2015)",
x= NULL,
y="") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))
)
Filtro de Hodrick-Prescott
A continuación aplicaremos el filtro de Hodrick-Prescott a una selección de regiones con el objetivo de comprobar la heterogeneidad de patrones de crecimiento existentes en el país. Como el código sigue unas pautas similares al realizado anteriormente evitaremos, por motivos de claridad, exponer dichos códigos.
Veamos el comportamiento de la región capitalina, Lima, en primer lugar. En tanto que esta región representa alrededor del 40% del VAB total del país y una tercera parte de la población, podemos inferir que el resultado agregado de la economía nacional estará notablemente influenciado por el de esta región. Esta hipótesis se comprueba en los gráficos siguientes donde observamos evidentes similitudes con los resultados obtenidos previamente para el total de la economía nacional.
Lima
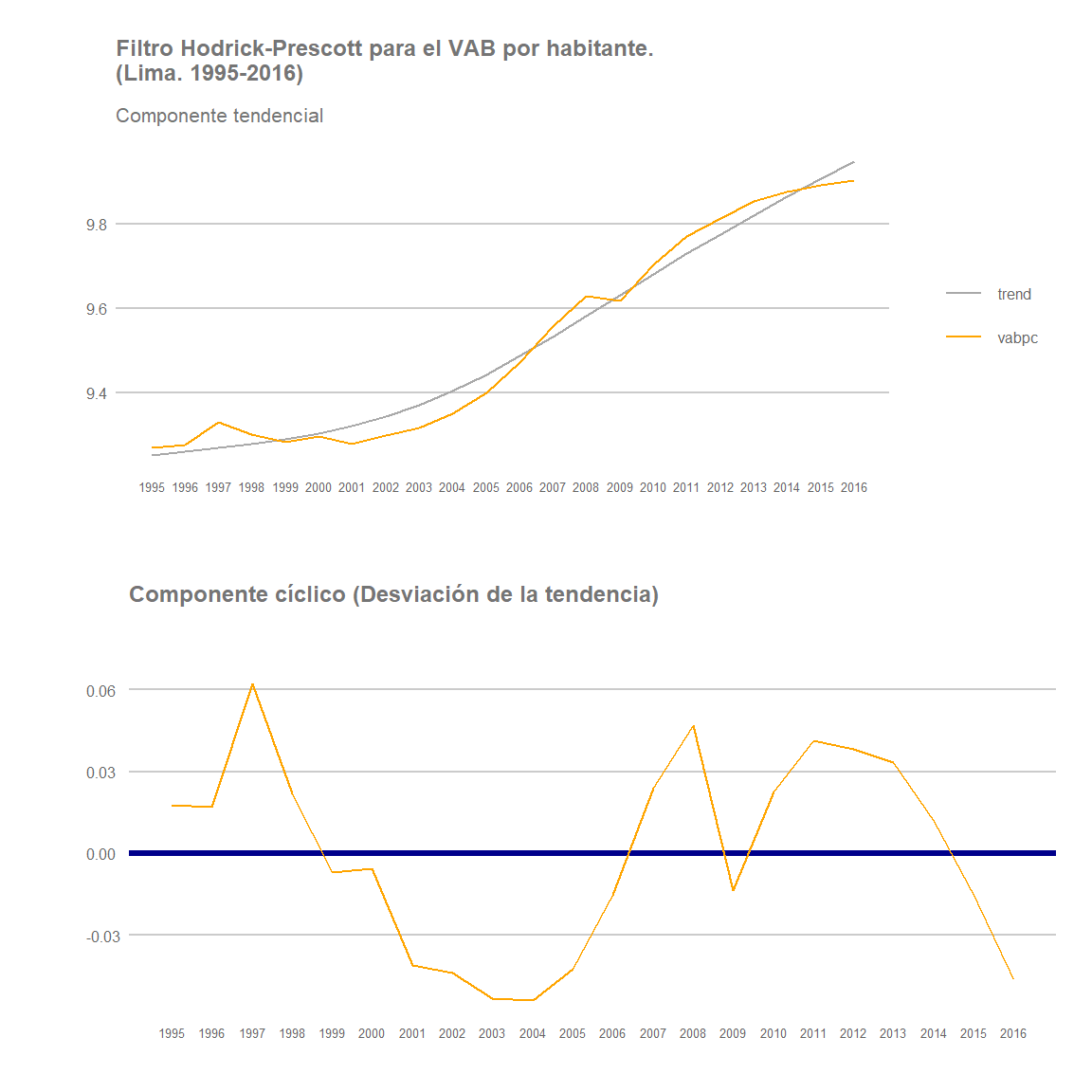
Por lo general, han sido las regiones costeras las que han registrado un mayor dinamismo durante el periodo analizado tal y como observamos en este post anterior. Veamos, por ejemplo, la evolución que han registrado otras dos regiones costeras: Ica y La Libertad. De nuevo, su trayectoria a lo largo del periodo muestra un patrón similar al de Lima y al del conjunto nacional: Una tendencia ascendente en términos de crecimiento de la renta por habitante, especialmente intensa a partir de los años 2003-2003, pero con señales de un posible estancamiento, o ralentización del crecimiento, al final del periodo.
Ica
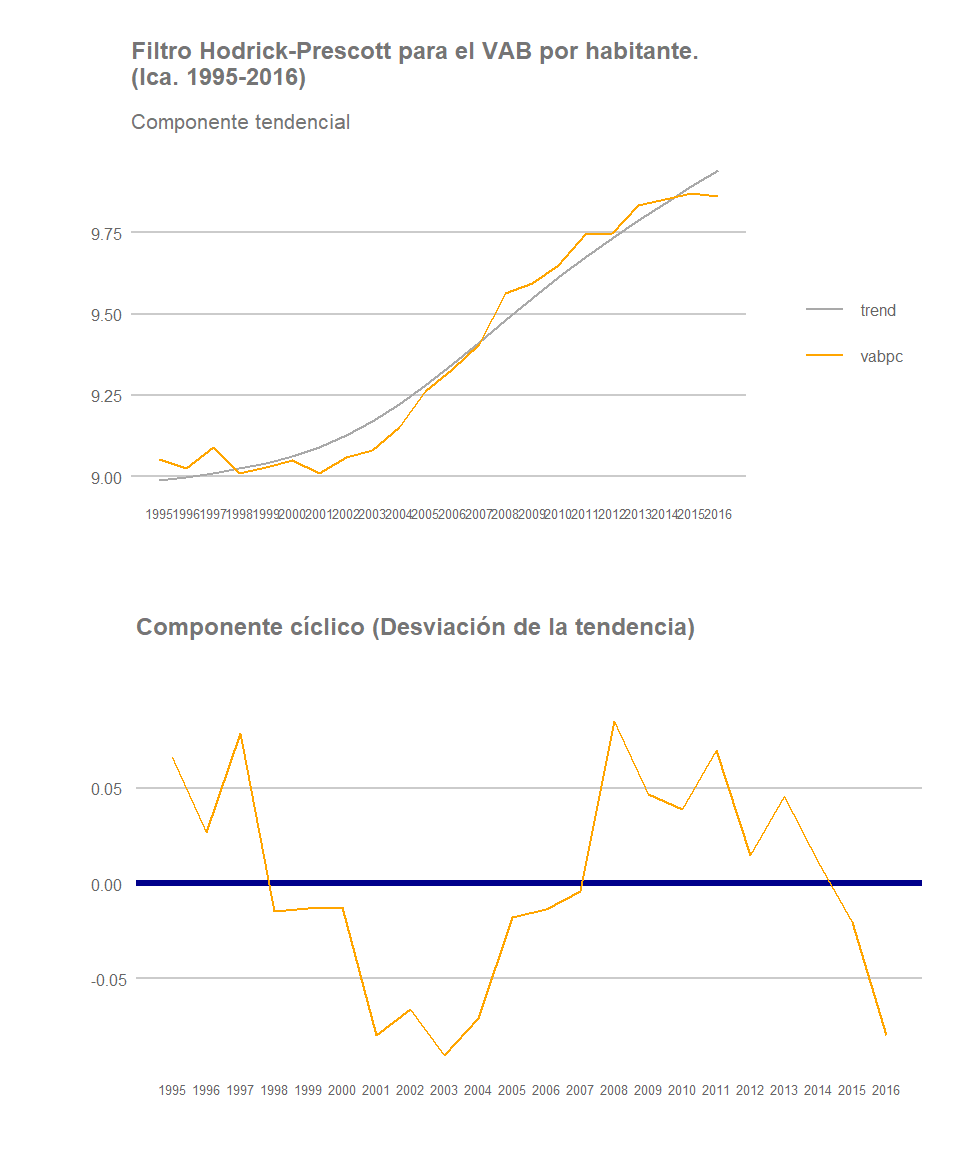
La Libertad
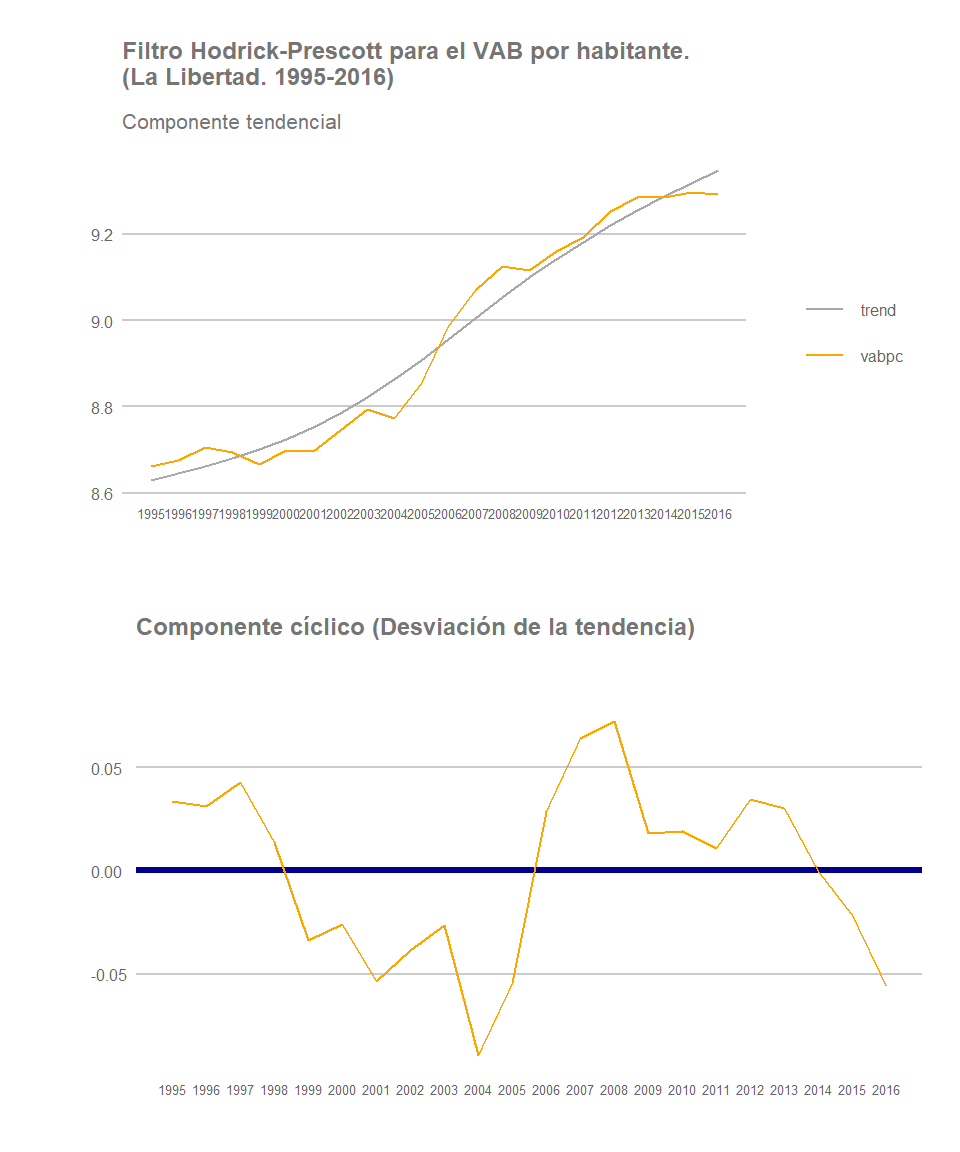
Aunque podría inferirse que las regiones costeras muestran patrones similares al del conjunto nacional, este no es el caso para todas ellas. Un ejemplo evidente es la región de Moquegua, departamento de pequeño tamaño y eminentemente cuprífero (y que gracias a ello presenta los mayores niveles de renta per cápita del país), pero que en los últimos años, debido a los proyectos de ampliación en el yacimiento de Cuajone y en la refinería de Illo, ha reducido su producción y tratamiento de cobre y molibdeno y, como consecuencia, ha registrado una notable ralentización de su crecimiento. Paradójicamente, el peor desempeño relativo de esta región de alto nivel de renta per cápita con respecto al resto de regiones constituye el factor principal de que haya tenido lugar una tendencia convergente en términos de renta por habitante en los últimos años en el país (ver este post). Algunos autores han bautizado a este tipo de dinámicas, donde la convergencia es resultado mayormente del peor comportamiento relativo de las regiones privilegiadas y no tanto del buen desempeño de las regiones inicialmente rezagadas, como convergencia depresiva o a la baja.
Moquegua
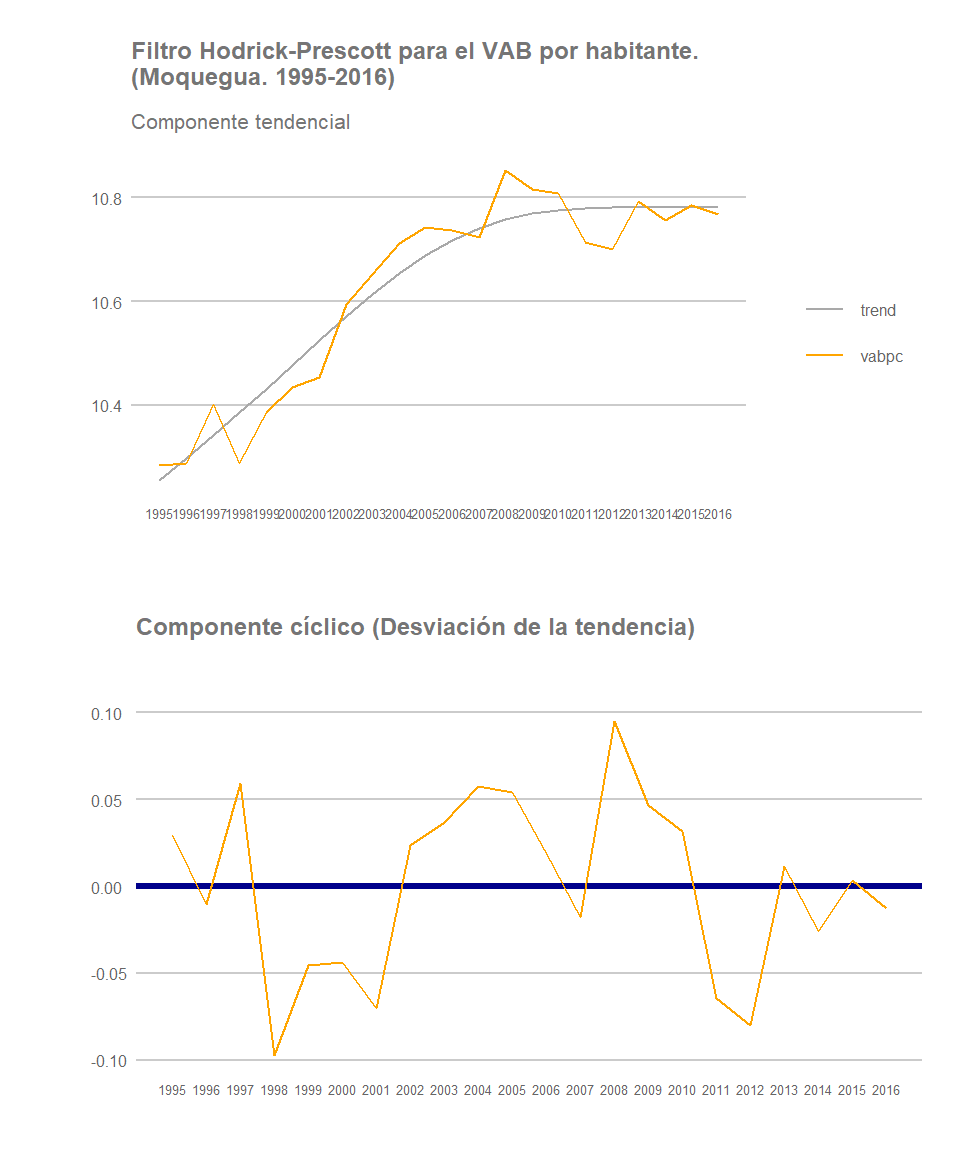
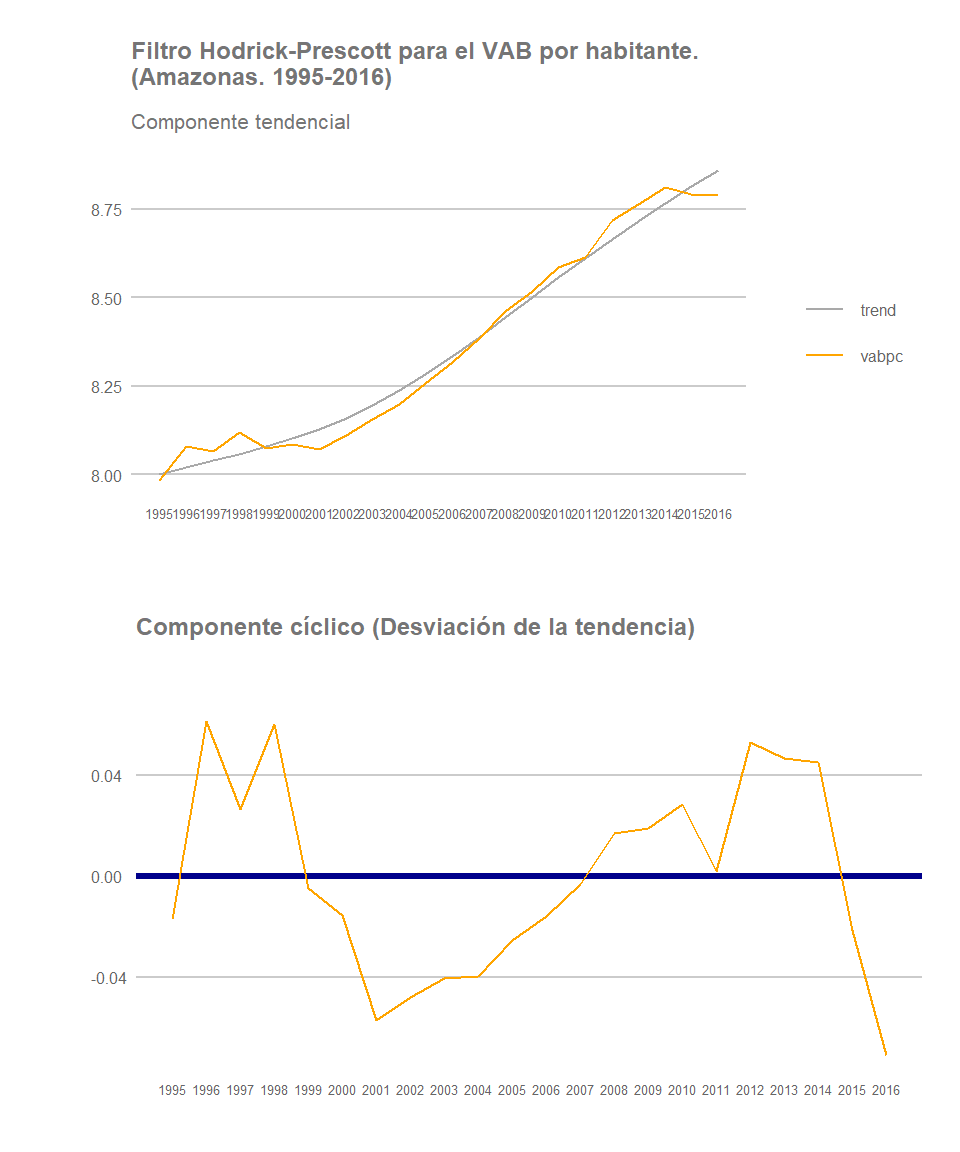
Una de las dinámicas que se han venido observando en los últimos años es que gran parte de las regiones selváticas se han ido configurando como focos de atracción de población. La expansión de terreno agrícola (ver post) o la aparición de nuevas oportunidades de empleo (no solo agrícolas sino también forestales, en la construcción, en los servicios o en la actividad minera entre otros) han servido de atracción de población de otras regiones, principalmente provenientes de la sierra del país. Veamos por ejemplo cómo se han comportado algunas regiones mayoritariamente selváticas: Amazonas, San Martín, Loreto y Madre de Dios.
Amazonas
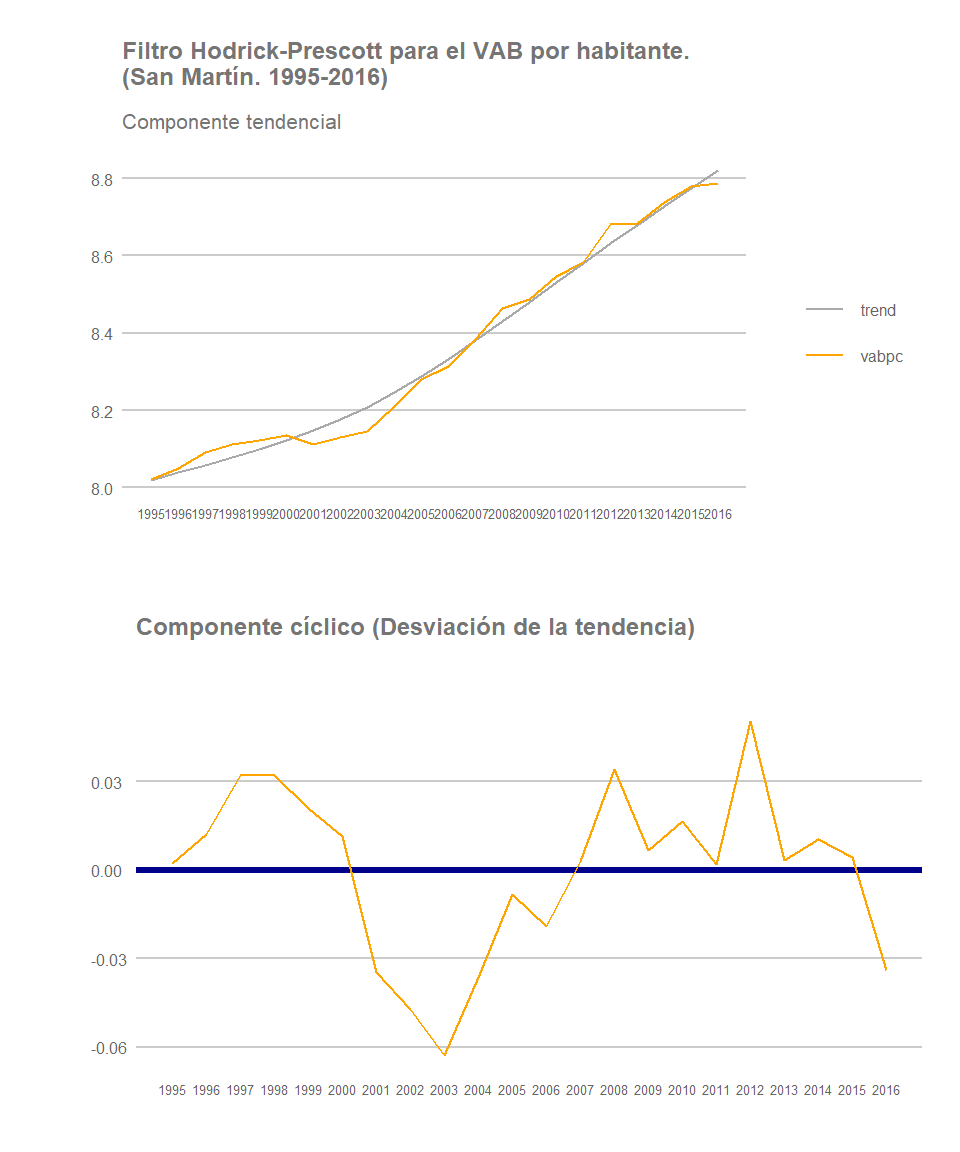
San Martín
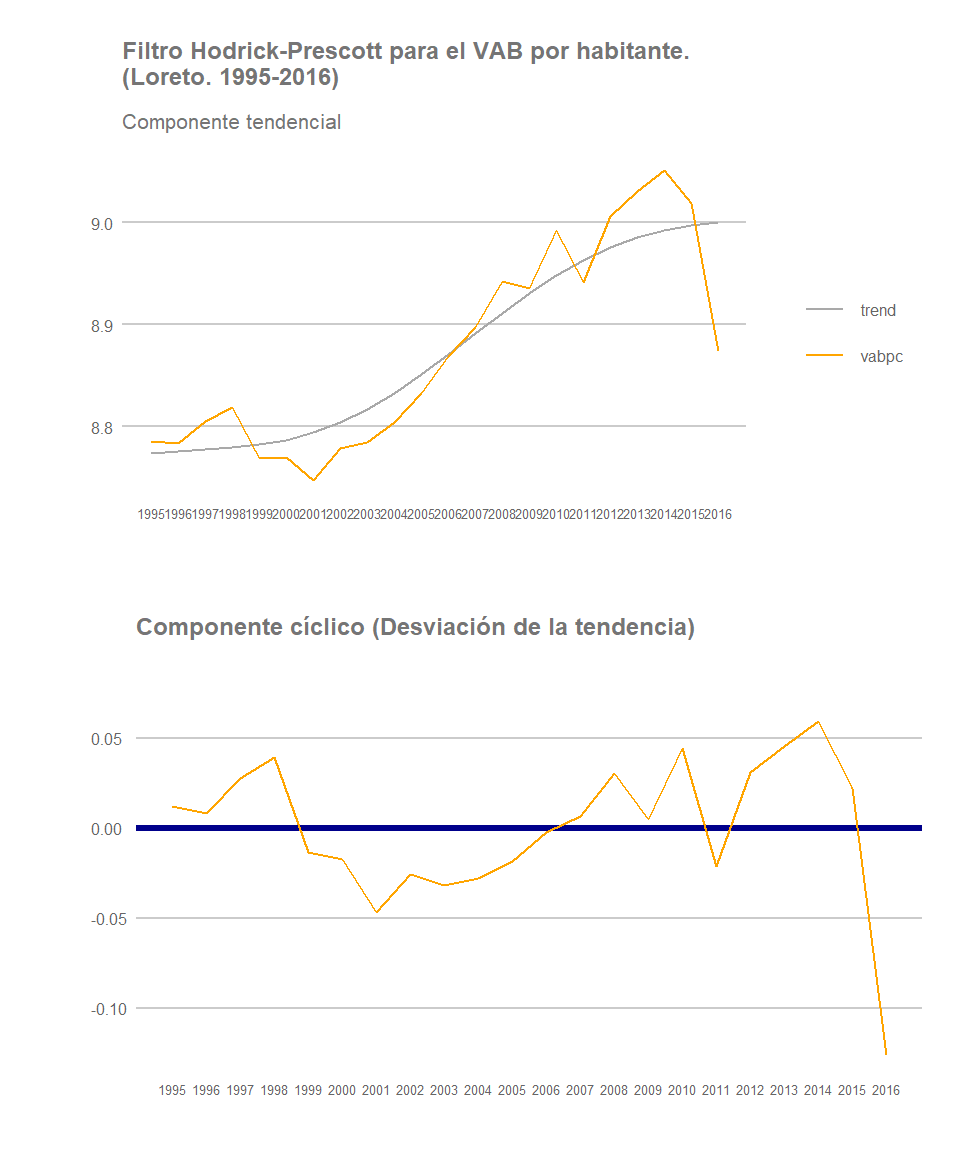
Loreto
Madre de Dios
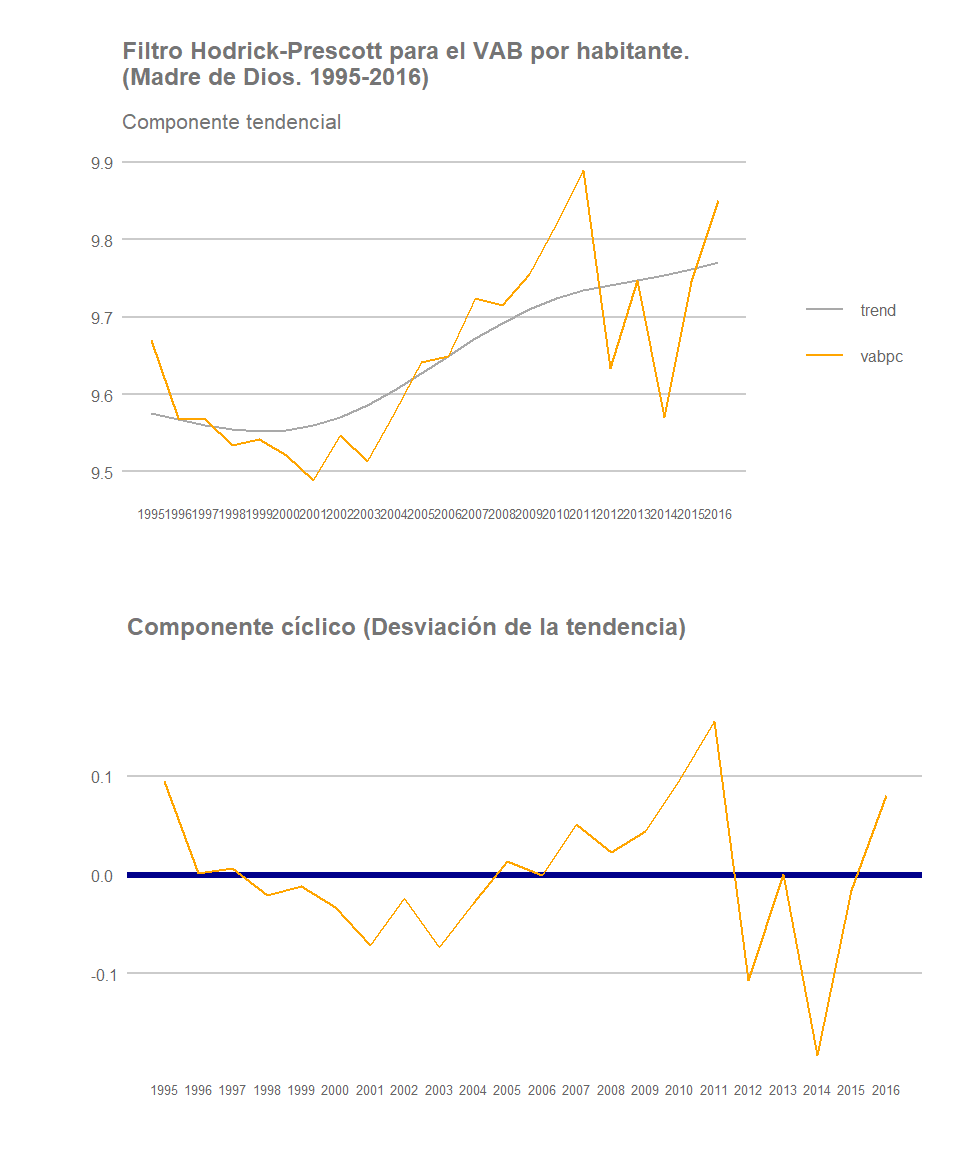
De nuevo no podemos realizar generalizaciones con respecto al conjunto de regiones selváticas. Si bien las regiones de Amazonas y San Martín registran un crecimiento estable de VABpc, con un componente cíclico que se asemeja al de Lima, Ica o La Libertad, Loreto y especialmente Madre de Dios presentan mayores altibajos, y un peor desempeño al final del periodo establecido. En Madre de Dios la lucha gubernamental contra la minería ilegal habrá tenido, sin lugar a dudas, un impacto significativo en el desempeño macroeconómico de la región. Loreto, por su parte, registra una cambio de tendencia y una caída significativa de su crecimiento anual al final del periodo analizado.
El comportamiento de las regiones de la sierra peruana registran también patrones de crecimiento diversos, aunque en gran medida su evolución tiende a estar muy vinculada al mayor o menor impulso de la actividad extractiva en estos territorios. La región de Cusco, por ejemplo, muestra una situación particular, dando muestran de un notable dinamismo económico que ha favorecido el incremento del VAB por habitante de dicha región durante la última década. El turismo (con la ciudadela inka del Machupichu y el Valle Sagrado como unos de los principales referentes turísticos del país), la construcción de viviendas en la capital de la región, los servicios y, especialmente, la extracción de gas (el gas de Camisea), han impulsado notablemente la economía de la región. Quiza debido a ello, al igual que sucede con regiones como Ica o Lima, su componente circular se asemeja también al de la economía nacional.
Cusco
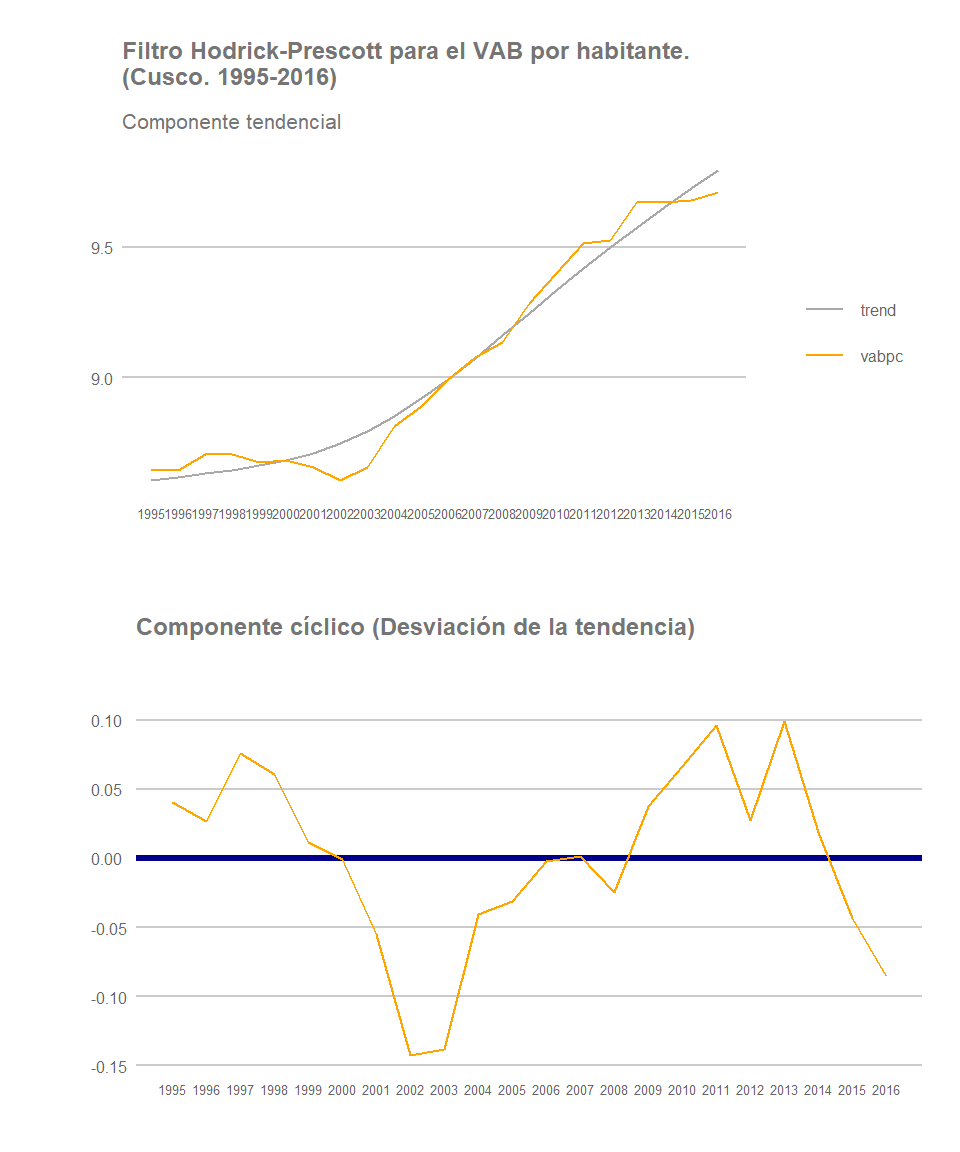
Sin embargo, como señalamos previamente, el desempeño de muchas de estas regiones en términos de VABpc se ve influenciada por el resultado que la actividad extractiva haya tenido en las mismas, evidentemente en aquellas regiones donde tenga lugar actividad minera y/o petrolera, el cual no ha sido homogéneo a lo largo y ancho del país. Es por ello que la región de Apurímac registra el fuerte incremento al final del periodo observado previamente, donde claramente el resultado de dicha actividad afecta al valor del VABpc del conjunto de la región, pero también explica en gran medida la ralentización del crecimiento del VABpc de Cajamarca o de Pasco, regiones de gran tradición minera pero donde ha tenido lugar una significativa reducción de la participación relativa del VAB generado por esta actividad en los últimos años. De hecho, aunque la especialización relativa del sector minero es especialmente significativa en ambas regiones, y también en otras como Madre de Dios, Ancash, Moquegua o Cusco, entre 2001 y 2012 la pérdida de participación relativa en términos reales del sector minero en el VAB total de Pasco se redujo en 13,4 puntos porcentuales y en Cajamarca en 11,25.
Apurímac
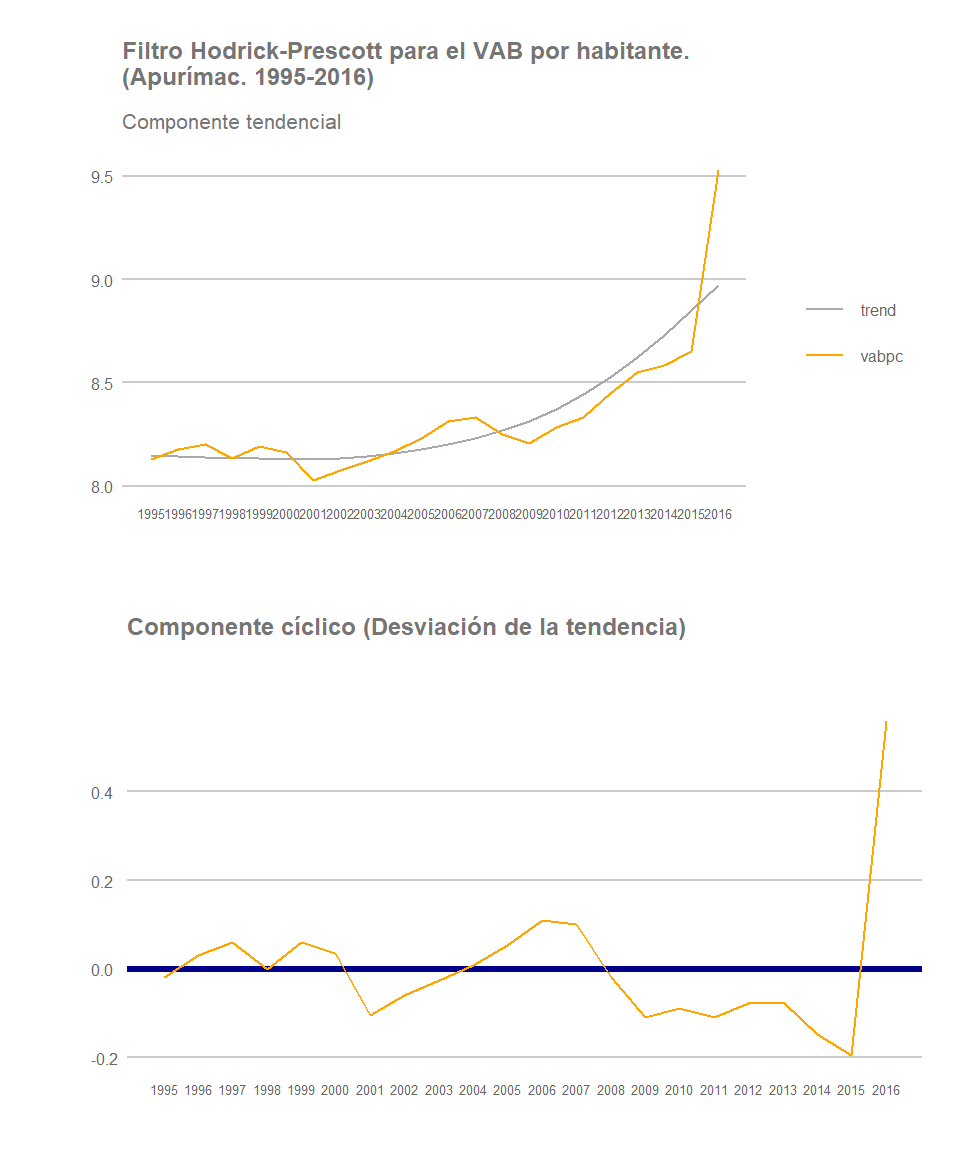
Cajamarca
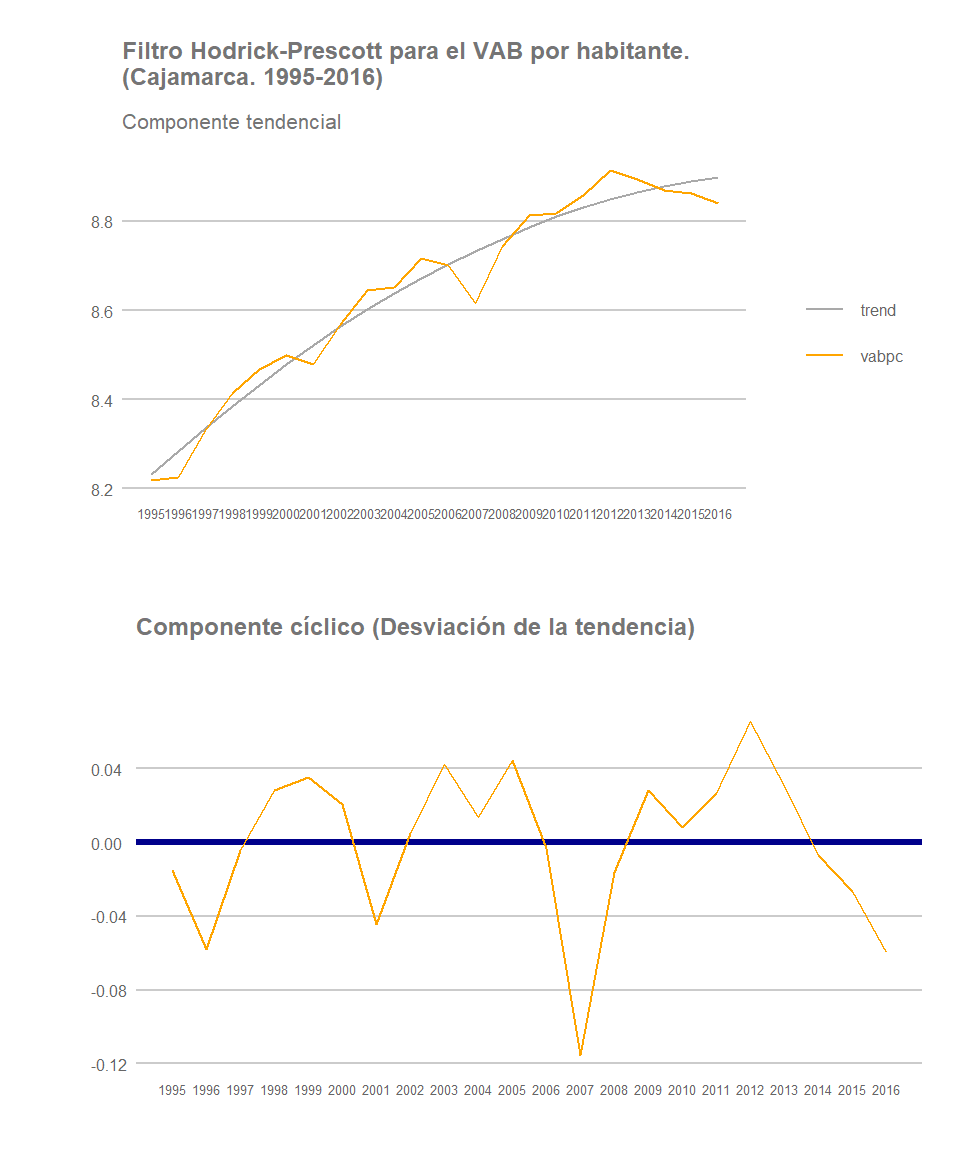
Pasco
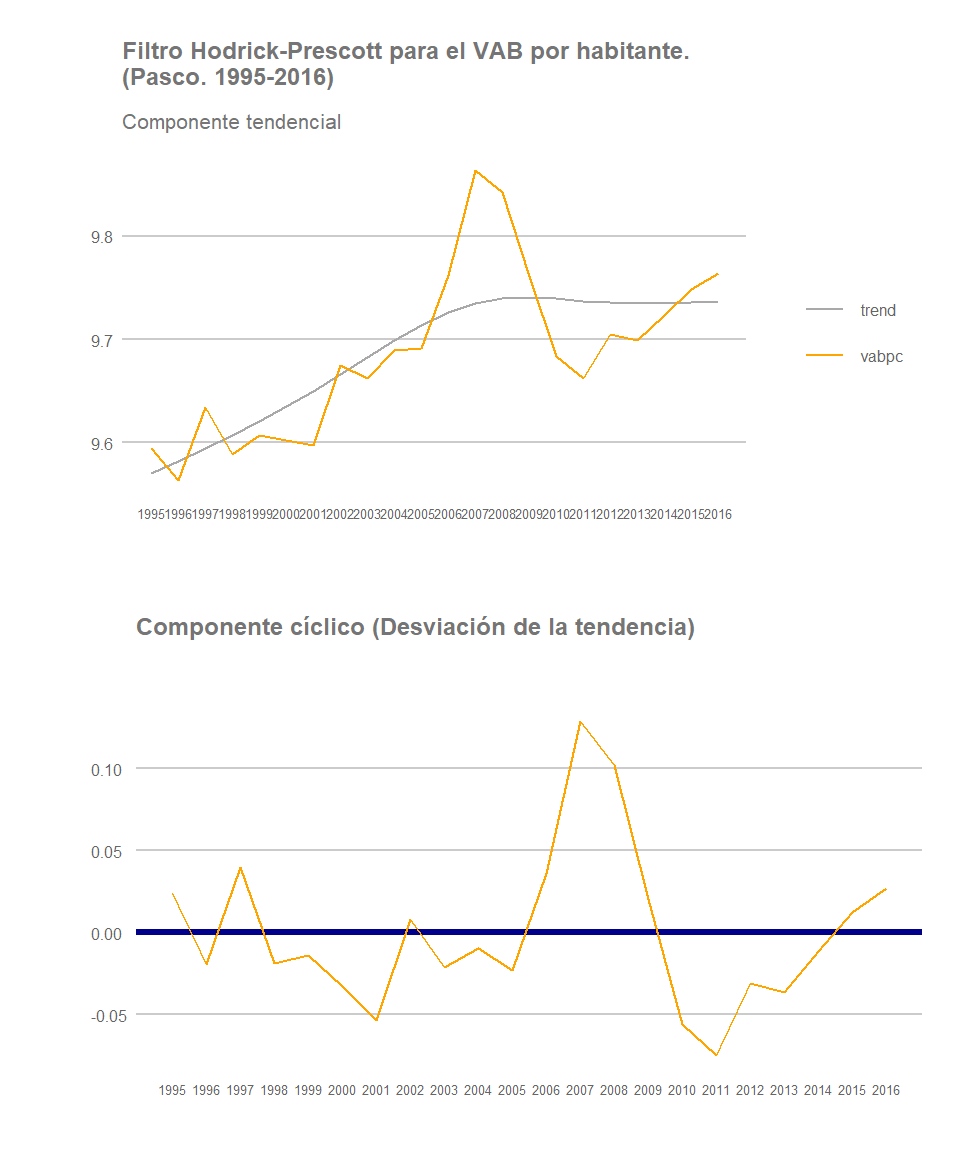
Comparación del componente cíclico
Tras examinar brevemente la evolución de algunas regiones, y constatar la heterogeneidad existente entre ellas, nos proponemos a representar conjuntamente los respectivos componentes de ciclo en un mismo gráfico con la finalidad de examinar si existen patrones similares en la evolución de este componente a lo largo del periodo. Realizaremos de nuevo el gráfico utilizando el paquete {plotly} por la misma razón que la expuesta previamente.
ggplotly(
cycles_df %>%
ggplot() +
geom_line(data = . %>% filter(Name != "PERU"), aes(date, ciclos, group = Name),
size = 0.5, alpha = 0.5, col = "grey") +
geom_line(data = . %>% filter(Name == "PERU"), aes(date, ciclos),
size = 1.5, col = "orange") +
scale_x_date(breaks = cycles_df$date, date_labels = "%Y") +
#scale_y_continuous(labels = scales::comma) +
labs(title= "Evolución del componente cíclico. \n(Perú y Regiones. 1995-2016)",
x= NULL,
y="") +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))
)
A continuación eliminamos el año 2016 como hicimos previamente con el objetivo de examinar la evolución sin que el comportamiento especial de Apurímac nos distorsione la imagen general.
A pesar de los ejercicios realizados encontramos, también en términos del componente cíclico del valor agregado bruto per cápita, comportamientos heterogéneos que se diferencian del comportamiento seguido por el conjunto de la economía. Para examinar qué regiones guardan una mayor semejanza realizaremos, en el siguiente apartado, un análisis de correlaciones.
Correlaciones del componente cíclico
Con la función {cor} podemos fácilmente estimar el grado de correlación del componente circular de cada una de las regiones con respecto al mismo componente de Perú a nivel nacional (o de otra región). Como habíamos observado previamente, Lima es la región que guarda una mayor correlación con la evolución nacional (0.970), aunque también es fuerte en regiones como Ica (0.916) o La Libertad (0.888). Por el contrario, regiones como Ancash, Junín o Cajamarca presentan valores muy bajos, e incluso negativos, es decir, poca correlación en su componente cíclico con respecto al de la economía en su conjunto.
cor(PERU.hp$cycle, AMA.hp$cycle)
## [1] 0.7419094
cor(PERU.hp$cycle, ANC.hp$cycle)
## [1] 0.004488245
cor(PERU.hp$cycle, APU.hp$cycle)
## [1] -0.1457461
cor(PERU.hp$cycle, ARE.hp$cycle)
## [1] 0.5788062
cor(PERU.hp$cycle, AYA.hp$cycle)
## [1] 0.7813229
cor(PERU.hp$cycle, CAJ.hp$cycle)
## [1] -0.03263734
cor(PERU.hp$cycle, CUS.hp$cycle)
## [1] 0.75623
cor(PERU.hp$cycle, HUAV.hp$cycle)
## [1] 0.5091527
cor(PERU.hp$cycle, HUAC.hp$cycle)
## [1] 0.3841819
cor(PERU.hp$cycle, ICA.hp$cycle)
## [1] 0.9169704
cor(PERU.hp$cycle, JUN.hp$cycle)
## [1] 0.1449506
cor(PERU.hp$cycle, LLIB.hp$cycle)
## [1] 0.8880598
cor(PERU.hp$cycle, LAM.hp$cycle)
## [1] 0.6925062
cor(PERU.hp$cycle, LIM.hp$cycle)
## [1] 0.9709954
cor(PERU.hp$cycle, LOR.hp$cycle)
## [1] 0.6409448
cor(PERU.hp$cycle, MDD.hp$cycle)
## [1] 0.3079624
cor(PERU.hp$cycle, MOQ.hp$cycle)
## [1] 0.0707616
cor(PERU.hp$cycle, PAS.hp$cycle)
## [1] 0.2734773
cor(PERU.hp$cycle, PIU.hp$cycle)
## [1] 0.9249462
cor(PERU.hp$cycle, PUN.hp$cycle)
## [1] 0.8237861
cor(PERU.hp$cycle, SMA.hp$cycle)
## [1] 0.7973064
cor(PERU.hp$cycle, TAC.hp$cycle)
## [1] 0.3224676
cor(PERU.hp$cycle, TUM.hp$cycle)
## [1] 0.7153841
cor(PERU.hp$cycle, UCA.hp$cycle)
## [1] 0.4781411
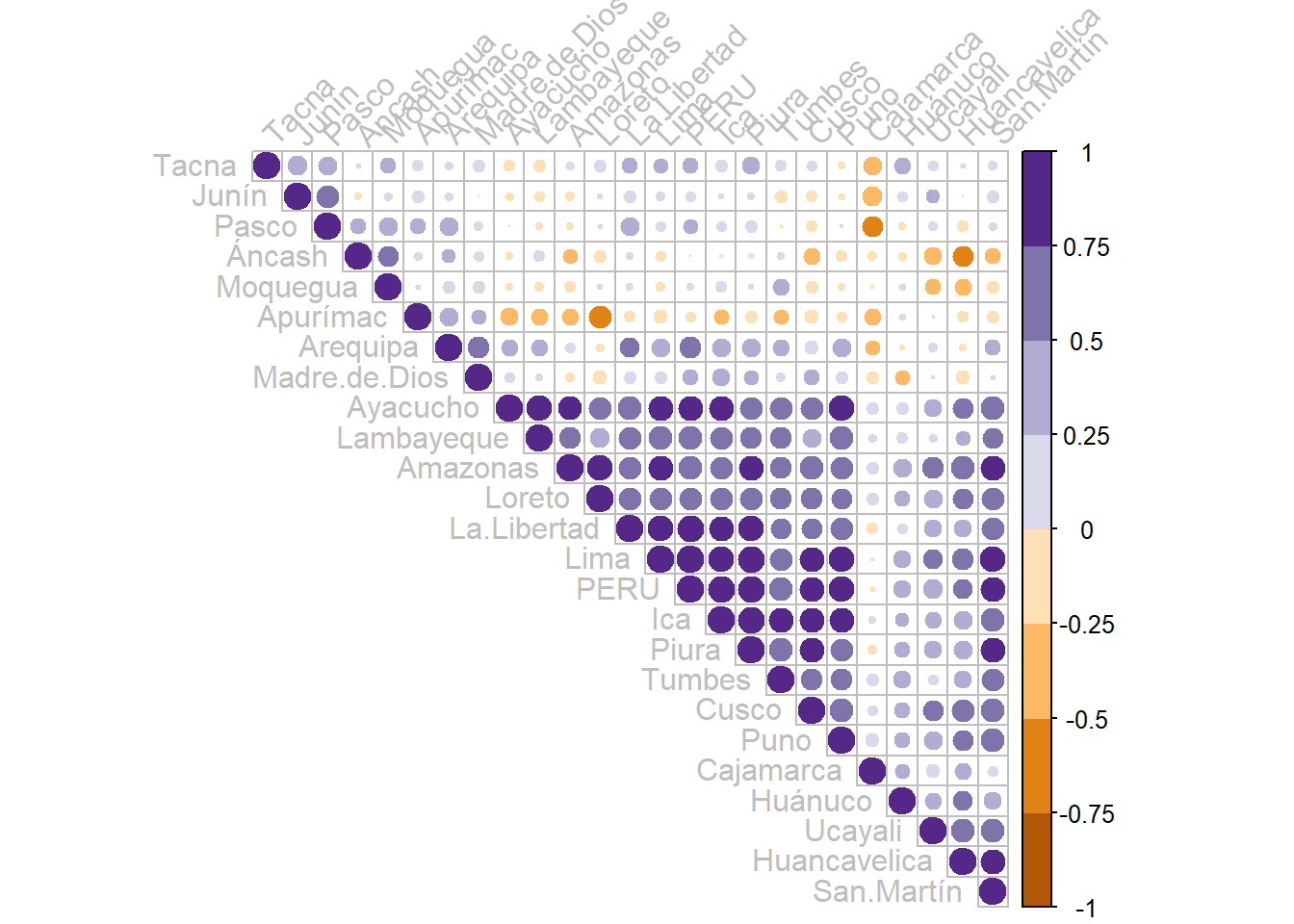
Los gráficos de correlación resultan de gran utilidad a la hora de representar en un solo gráfico todos los valores de forma conjunta. Para ello una posibilidad consiste en utilizar la función corrplot() del paquete del mismo nombre. El resultado nos permite observar de una forma muy intuitiva las regiones cuyo componente cíclico de la evolución de sus respectivos VAB por habitante guardan una mayor similitud con respecto a la evolución nacional o en relación a otras regiones. Del mismo modo podemos identificar regiones, como es por ejemplo el caso de Cajamarca, cuyo componente cíclico no parece guardar ningún tipo de similitud con ninguna otra región del país.
mydata.cor <- cor(cycles)
corrplot(mydata.cor,
type = "upper",
order="hclust",
tl.col = "grey",
tl.srt = 45,
col= brewer.pal(n=8, name = "PuOr"))