Librerías y datasets
library(tidyverse)
library(ggthemes)
library(ggthemr)
library(ggrepel)
library(ggplot2)
library(dplyr)
library(readxl)
library(DT)
library(plotly)
library(leaflet)
library(IC2)
library(REAT)
library(pastecs)
library(psych)
library(ineq)
library(viridis)
library(sf)
library(raster)
library(ggiraph)
options(scipen = 999)
#theme:
source("https://github.com/traffordDataLab/assets/raw/master/theme/ggplot2/theme_lab.R")
# DATASET: VAB per capita (precios de 1994):
paper95_16 <- read_excel("C:/Users/Usuario/Desktop/r_que_r/r_que_r/content/datasets/paper95_16.xlsx")
Peru_VABpc2 <- paper95_16 %>%
gather(key = year, value = vabpc, 5:26)
datatable(Peru_VABpc2)
# DATASET: VAB percapita (precios de 2007)
BD_VABpc <- read_excel("C:/Users/Usuario/Desktop/r_que_r/r_que_r/content/datasets/1995_2016_VABPC_de07.xlsx")
Peru_VABpc <- BD_VABpc %>%
gather(key = year, value = vabpc, 4:25)
datatable(Peru_VABpc)
Mapa de Perú
En primer lugar conviene presentar un mapa del país con su principal división administrativa. Perú se divide en 24 regiones más el Callao y la Provincia de Lima (o Lima Metropolitana). El Callao es su propia región, y contiene one provincia: la Provincia Constitucional del Callao. La capital de la Provincia de Lima es Lima, que también es la capital del país. En nuestro ejercicio tanto el Callao como Lima Metropólitana se incluirán dentro de la región de Lima.
Nótese que cada región en el mapa redirige a su entrada en Wikipedia, con información sobre la región seleccionada.
PER_1 <- getData("GADM", country ="PE", level =1)
PERU_1_df <-broom::tidy(PER_1, region = "NAME_1")
##### Plot with animated tooltip:
# link to wikipedia:
PERU_1_df$onclick <- sprintf("window.open(\"%s%s\")",
"http://en.wikipedia.org/wiki/", as.character(PERU_1_df$id))
#plot:
m <- ggplot() +
labs(title = "Peru: Regiones",
subtitle = "(con links a Wikipedia)",
fill = NULL) +
geom_polygon_interactive(data = PERU_1_df,
aes(x = long, y = lat, group = group,
tooltip = id, data_id = id, onclick = onclick),
fill = "orange",
color = "white",
size = 0.2,
alpha = 0.8) +
coord_map() +
theme_void()+
theme(
axis.line = element_blank(),
axis.text = element_blank(),
axis.title = element_blank(),
axis.ticks = element_blank(),
plot.background = element_rect(fill = "snow", color = NA),
panel.background = element_rect(fill= "snow", color = NA),
plot.title = element_text(size = 16, hjust = 0.5),
plot.subtitle = element_text(size = 12, hjust = 0.5),
plot.caption = element_text(size = 8, hjust = 1),
legend.title = element_text(color = "grey40", size = 8),
legend.text = element_text(color = "grey40", size = 7, hjust = 0),
legend.position = c(0.05, 0.25),
plot.margin = unit(c(0.5,2,0.5,1), "cm")) +
guides(fill = FALSE)
widgetframe::frameWidget(ggiraph(code=print(m), width = 0.6, hover_css = "cursor:pointer;fill:lightgrey;stroke:darkgrey;"))
Existen diversas formas de analizar las disparidades regionales en un país en un determinado año o a lo largo del tiempo, y de representar dichas disparidades gráficamente. No obstante, cada una de ellas tiene sus fortalezas y sus debilidades por lo que conviene realizar el análisis utilizando diversas herramientas de análisis y distintos indicadores. Nótese que en esta ocasión las disparidades van a ser entendidas como las diferencias entre regiones en términos de VAB per cápita, aunque existen otras posibles variables que podrían también resultar de interés, como por ejemplo el nivel de productividad del trabajo. En primer lugar, para hacernos una idea de la magnitud de las disparidades, podemos, por ejemplo, representar el valor de cada región en el año inicial y final del periodo analizado. Observando los gráficos para cada año resulta patente que algunas de las regiones costeras, principalmente Moquegua, se han consolidado como lideres (las de mayor renta por habitante) con el paso de los años.
bar_plot <- BD_VABpc %>%
dplyr::select(Name, Geo, `1995`, `2016`) %>%
gather(key = year, value = vabpc, 3:4)
ggthemr("flat")
ggplot(bar_plot,
aes(x= reorder(Name, vabpc, max),
y = vabpc, fill= Geo)) +
geom_col() +
facet_wrap(.~year, scales = "free_y") +
coord_flip() +
theme_minimal() +
scale_y_continuous(labels = scales::comma) +
geom_text(aes(label = vabpc),
hjust = 1.2,
size = 2,
color = "white",
fontface = "bold") +
labs(title = "VAB per cápita por región en 1995 y 2016",
subtitle = "(valores constantes de 2007)",
x = NULL,
y = "VAB por habitante",
fill = NULL) +
theme(legend.position = "bottom",
plot.title=element_text(size = 12,
hjust = 0.5),
plot.subtitle = element_text(size = 10,
hjust = 0.5),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
axis.text.x=element_text(colour="black",
size = 8),
axis.text.y=element_text(colour="black",
size = 8)) 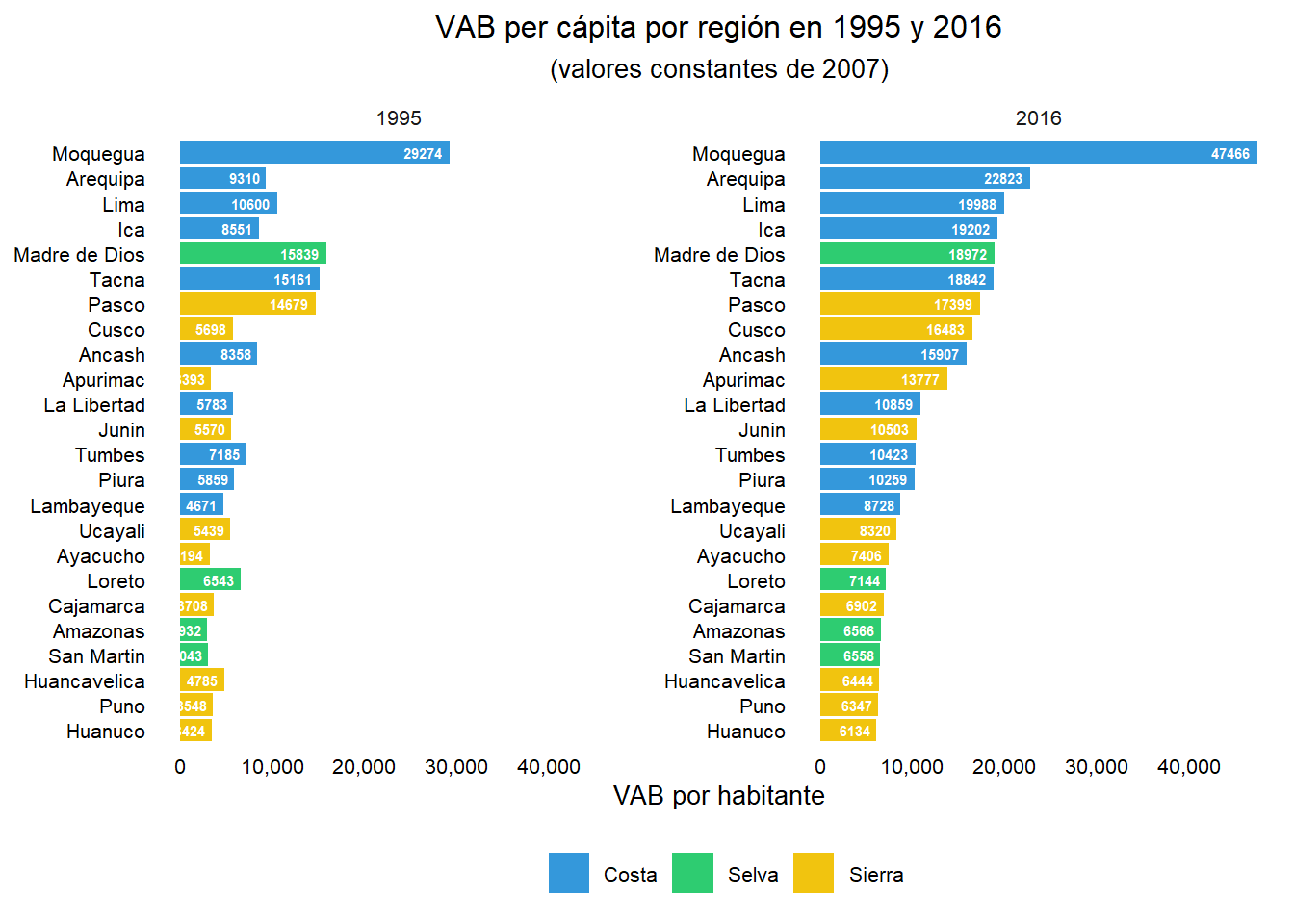
ggthemr_reset()
Los diagramas de caja (también llamados boxplots, o box and whisker plots), son otra forma en la que podemos examinar las diferencias existentes entre regiones, a la vez que observamos el valor de algunos indicadores estadísticos, como la media, la mediana o el rango intercuantílico de nuestras observaciones. Por ejemplo, vemos en el gráfico siguiente las diferencias existentes entre el grupo de regiones de mayor renta per cápita, regiones costeras (Moquegua, Lima, Arequipa, Ica y Tacna), con respecto al resto del país, especialmente con respecto a regiones como Apurímac, Huánuco, Puno y Ayacucho, regiones situadas en la sierra del país. Por su parte, un mayor rango intercuantil será indicativo de un mayor crecimiento durante el periodo, como sucede en el caso de Cusco que muestra un mayor dinamismo en comparación con otras regiones de similar nivel de renta por habitante. Nótese que los valores del gráfico están representados en escala logarítmica.
Peru_VABpc2 <- paper95_16 %>%
gather(key = year, value = vabpc, 5:26)
x <- ggplot(Peru_VABpc2, aes(x=Region, y=vabpc, fill = Geo)) +
geom_point(position = "jitter", alpha = 0.4, color = "violet") +
geom_boxplot(alpha = 0.6) +
scale_fill_manual(values = c("steelblue1", "limegreen", "orange")) +
stat_summary(fun="mean", geom="point",shape=23, fill="purple") +
scale_x_discrete(limits=c("Moquegua","Lima","Arequipa","Ica","Tacna","Pasco","Áncash","La Libertad","Madre de Dios","Junín","Cusco","Piura","Lambayeque","Ucayali","Tumbes","Loreto","Amazonas","Cajamarca","San Martín","Huancavelica","Ayacucho","Puno","Huánuco","Apurímac")) +
scale_y_continuous(trans = 'log10', labels = scales::comma) +
labs(title= "VAB per cápita por región 1995-2016",
subtitle="soles de 1994",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y=" VAB per cápita (log)",
fill = NULL) +
theme_lab() +
geom_hline(aes(yintercept=3450),colour="darkorange", linetype="dashed") +
geom_hline(aes(yintercept=6328),colour="darkorange", linetype="dashed") +
theme(axis.text.x = element_text(face = "bold",
colour = "grey60",
size = rel(0.9),
angle = 45,
hjust = 1),
axis.text.y=element_text(colour="grey60",
size = rel(0.8)),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 10,
hjust = 0),
text = element_text(size = 10)) +
annotate(geom = "curve", x = "Cajamarca", y = 6328,
xend= "San Martín", yend= 8000,
curvature = -0.25, color = "grey60") +
annotate(geom = "text", x= "Ayacucho", y = 8000,
size = rel(3), color = "grey60",
label = "VABpc promedio en 2016: 6,328 \n") +
annotate(geom = "curve", x = "Lima", y = 3450,
xend= "Arequipa", yend= 2800,
curvature = -0.25, color = "grey60") +
annotate(geom = "text", x= "Ica", y = 2750,
size = rel(3), color = "grey60",
label = "\n VABpc promedio en 1995: 3,450")
x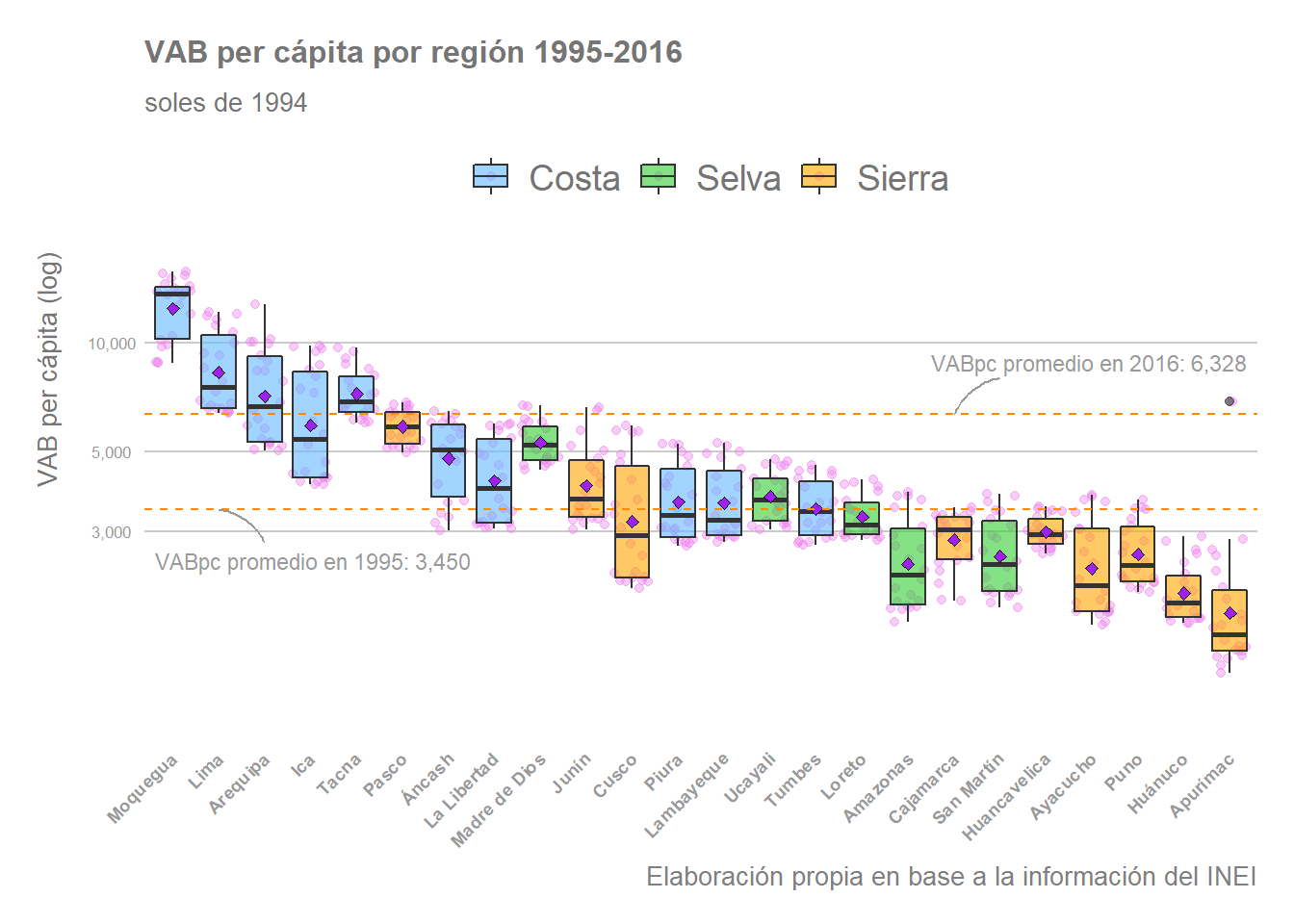
Podemos hacer que el gráfico sea interactivo de forma muy sencilla con el paquete {plotly} de la siguiente forma:
ggplotly(x)
Examinando la distribución
Existen numerosos paquetes en R que nos permiten obtener el resultado de diversos indicadores estadísticos descriptivos (media, mediana, mínimo, máximo, desviación estándar, asimetría, curtosis, etc.). Estos indicadores nos sirven para observar distintas características de la distribución de las observaciones así como su evolución a lo largo del periodo de tiempo estudiado. Veamos algunas posibilidades:
Una posibilidad es utilizar la función stat_desc() del paquete {pastecs}:
VABpc1995<- BD_VABpc$'1995'
VABpc1996<- BD_VABpc$'1996'
VABpc1997<- BD_VABpc$'1997'
VABpc1998<- BD_VABpc$'1998'
VABpc1999<- BD_VABpc$'1999'
VABpc2000<- BD_VABpc$'2000'
VABpc2001<- BD_VABpc$'2001'
VABpc2002<- BD_VABpc$'2002'
VABpc2003<- BD_VABpc$'2003'
VABpc2004<- BD_VABpc$'2004'
VABpc2005<- BD_VABpc$'2005'
VABpc2006<- BD_VABpc$'2006'
VABpc2007<- BD_VABpc$'2007'
VABpc2008<- BD_VABpc$'2008'
VABpc2009<- BD_VABpc$'2009'
VABpc2010<- BD_VABpc$'2010'
VABpc2011<- BD_VABpc$'2011'
VABpc2012<- BD_VABpc$'2012'
VABpc2013<- BD_VABpc$'2013'
VABpc2014<- BD_VABpc$'2014'
VABpc2015<- BD_VABpc$'2015'
VABpc2016<- BD_VABpc$'2016'
peruvars <- data.frame(VABpc1995, VABpc1996, VABpc1997, VABpc1998, VABpc1999, VABpc2000, VABpc2001, VABpc2002, VABpc2003, VABpc2004, VABpc2005, VABpc2006, VABpc2007, VABpc2008, VABpc2009, VABpc2010, VABpc2011, VABpc2012, VABpc2013, VABpc2014, VABpc2015, VABpc2016)
statsperu <- stat.desc(peruvars, norm = TRUE)
statsperu$VABpc1995<-round(statsperu$VABpc1995,3)
statsperu$VABpc1996<-round(statsperu$VABpc1996,3)
statsperu$VABpc1997<-round(statsperu$VABpc1997,3)
statsperu$VABpc1998<-round(statsperu$VABpc1998,3)
statsperu$VABpc1999<-round(statsperu$VABpc1999,3)
statsperu$VABpc2000<-round(statsperu$VABpc2000,3)
statsperu$VABpc2001<-round(statsperu$VABpc2001,3)
statsperu$VABpc2002<-round(statsperu$VABpc2002,3)
statsperu$VABpc2003<-round(statsperu$VABpc2003,3)
statsperu$VABpc2004<-round(statsperu$VABpc2004,3)
statsperu$VABpc2005<-round(statsperu$VABpc2005,3)
statsperu$VABpc2006<-round(statsperu$VABpc2006,3)
statsperu$VABpc2007<-round(statsperu$VABpc2007,3)
statsperu$VABpc2008<-round(statsperu$VABpc2008,3)
statsperu$VABpc2009<-round(statsperu$VABpc2009,3)
statsperu$VABpc2010<-round(statsperu$VABpc2010,3)
statsperu$VABpc2011<-round(statsperu$VABpc2011,3)
statsperu$VABpc2012<-round(statsperu$VABpc2012,3)
statsperu$VABpc2013<-round(statsperu$VABpc2013,3)
statsperu$VABpc2014<-round(statsperu$VABpc2014,3)
statsperu$VABpc2015<-round(statsperu$VABpc2015,3)
statsperu$VABpc2016<-round(statsperu$VABpc2016,3)
Los resultados obtenidos para los años 1995, 2000, 2005, 2010 y 2016 serán:
statsperu_selection <- statsperu %>%
dplyr::select(VABpc1995, VABpc2000, VABpc2005, VABpc2010, VABpc2016)
datatable(statsperu_selection)
Una segunda posibilidad para obtener estadísticos descriptivos es utilizando la función describe() del paquete {psych}.
statsperu2 <- describe(peruvars)
statsperu2
## vars n mean sd median trimmed mad min max range
## VABpc1995 1 24 7772.79 5981.20 5740.5 6772.95 3457.42 2932 29274 26342
## VABpc1996 2 24 7758.29 5862.10 5778.5 6766.45 3363.28 3135 29374 26239
## VABpc1997 3 24 8152.21 6473.14 5997.0 7039.90 3466.32 3184 32902 29718
## VABpc1998 4 24 7798.04 5782.18 6007.5 6823.95 3344.00 3331 29391 26060
## VABpc1999 5 24 7982.75 6277.36 5841.5 6887.40 3355.87 3212 32395 29183
## VABpc2000 6 24 8039.50 6534.47 5922.0 6875.55 3507.83 3251 33984 30733
## VABpc2001 7 24 7978.58 6696.38 5764.5 6790.60 3427.77 3058 34693 31635
## VABpc2002 8 24 8499.88 7703.81 5764.0 7081.95 3285.44 3213 39901 36688
## VABpc2003 9 24 8732.46 8080.78 5859.0 7241.25 3111.98 3353 42245 38892
## VABpc2004 10 24 9109.58 8582.78 6372.5 7523.20 3883.67 3521 44865 41344
## VABpc2005 11 24 9538.33 8816.25 6630.5 7942.00 3971.14 3757 46289 42532
## VABpc2006 12 24 9895.58 8763.48 6987.0 8306.70 4206.14 3925 45993 42068
## VABpc2007 13 24 10412.33 8780.42 7323.5 8858.00 4298.80 3980 45367 41387
## VABpc2008 14 24 11139.58 9824.86 7808.5 9437.90 4533.05 3825 51687 47862
## VABpc2009 15 24 11109.04 9395.90 7787.0 9576.30 4306.21 3656 49811 46155
## VABpc2010 16 24 11512.54 9315.37 8289.0 10001.05 4643.50 3952 49411 45459
## VABpc2011 17 24 11673.17 8619.52 8407.5 10325.80 4493.76 4160 45003 40843
## VABpc2012 18 24 11935.21 8281.96 8819.5 10695.60 4544.17 4671 44360 39689
## VABpc2013 19 24 12566.71 9101.12 9067.0 11163.60 4643.50 5156 48653 43497
## VABpc2014 20 24 12475.58 8708.01 9751.0 11106.30 5347.74 5338 46866 41528
## VABpc2015 21 24 12923.75 9020.78 10456.0 11524.50 6223.95 5731 48241 42510
## VABpc2016 22 24 13477.17 8996.95 10463.0 12034.10 5874.06 6134 47466 41332
## skew kurtosis se
## VABpc1995 2.04 4.37 1220.91
## VABpc1996 2.15 5.03 1196.60
## VABpc1997 2.36 6.15 1321.32
## VABpc1998 2.23 5.41 1180.28
## VABpc1999 2.47 6.74 1281.36
## VABpc2000 2.61 7.52 1333.84
## VABpc2001 2.64 7.71 1366.89
## VABpc2002 2.81 8.62 1572.53
## VABpc2003 2.95 9.42 1649.48
## VABpc2004 2.98 9.64 1751.95
## VABpc2005 2.98 9.66 1799.61
## VABpc2006 2.87 9.09 1788.84
## VABpc2007 2.60 7.61 1792.29
## VABpc2008 2.87 9.18 2005.49
## VABpc2009 2.84 9.09 1917.93
## VABpc2010 2.73 8.52 1901.49
## VABpc2011 2.35 6.48 1759.45
## VABpc2012 2.42 6.94 1690.55
## VABpc2013 2.52 7.42 1857.76
## VABpc2014 2.50 7.28 1777.52
## VABpc2015 2.43 6.93 1841.36
## VABpc2016 2.18 5.69 1836.49
Veamos gráficamente la evolución de alguno de estos indicadores. En primer lugar observemos la evolución de la media, la media truncada, la mediana, el valor máximo y el valor mínimo del VAB por habitante entre 1995 y 2016. Del resultado obtenido (ver gráfico) podemos destacar algunas conclusiones. En primer lugar resulta patente la gran brecha existente entre el valor máximo y el valor mínimo, especialmente si tenemos en cuenta que los valores se encuentran de nuevo en escala logarítmica. Siendo que la mediana es inferior a la media, e incluso a la media truncada, podemos inferir que la mayor parte de los valores se encuentran más cercanos al valor mínimo, habiendo un número reducido de observaciones con valores muy superiores al de la mayoría, que presionan al alza el valor de la media del conjunto de regiones. Por consiguiente, aunque la media y la mediana han registrado una tendencia ascendente, las diferencias entre los valores superiores e inferiores se mantienen a lo largo del periodo. Dicho esto, nótese que la brecha entre el valor máximo y mínimo parece haberse reducido ligeramente entre 2008 y 2016, lo que puede haber contribuido al incremento de la media del conjunto de territorios del país.
vars_one <- statsperu2 %>%
mutate(year= c(1995:2016)) %>%
dplyr::select(year, mean, trimmed, median, max, min, range) %>%
gather(key = variable, value = valor, 2:7) %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
ggthemr("flat")
ggplot(vars_one, aes(x= year, y= valor, color = variable)) +
geom_line(size = 1) +
geom_point(size = 2) +
scale_x_date(breaks = vars_one$year, date_labels = "%Y") +
scale_y_continuous(trans = 'log10', labels = scales::comma) +
labs(title= "Media, media truncada, mediana, rango, valor máximo y mínimo. \n(Regiones. 1995-2016)",
subtitle="soles de 1994 (escala logarítmica)",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="Valor (log)",
color = NULL) +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))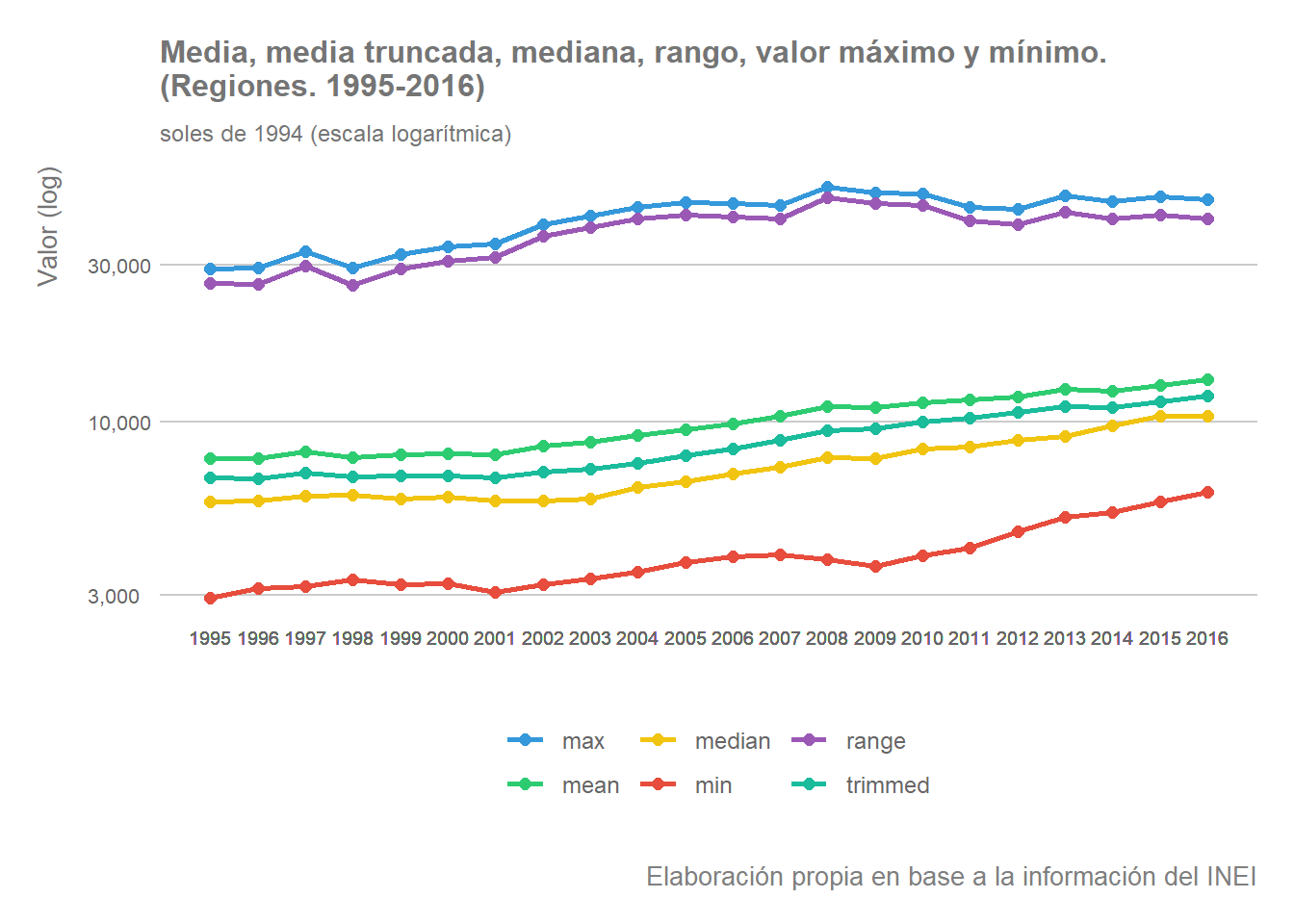
En el siguiente gráfico representamos la evolución de la desviación estándar y la desviación absoluta de la mediana. Como sabemos, una desviación estándar baja sería indicativo de que la mayor parte de regiones se encontrarían agrupadas con respecto a la media, mientras que una desviación estándar alta indicará que el VAB per cápita de las regiones se extiende sobre un rango mayor. Por su parte, la desviación absoluta de la mediana representa la dispersión con respecto a la mediana del conjunto de observaciones.
vars_two <- statsperu2 %>%
mutate(year= c(1995:2016)) %>%
dplyr::select(year, sd, mad) %>%
gather(key = variable, value = valor, 2:3) %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
ggplot(vars_two, aes(x= year, y= valor, color = variable)) +
geom_line(size = 1) +
geom_point(size = 2) +
scale_x_date(breaks = vars_one$year, date_labels = "%Y") +
scale_y_continuous(labels = scales::comma) +
labs(title= "Desviación estándar, desviación absoluta de la mediana, . \n(Regiones. 1995-2016",
subtitle="",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="Valor (log)",
color = NULL) +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))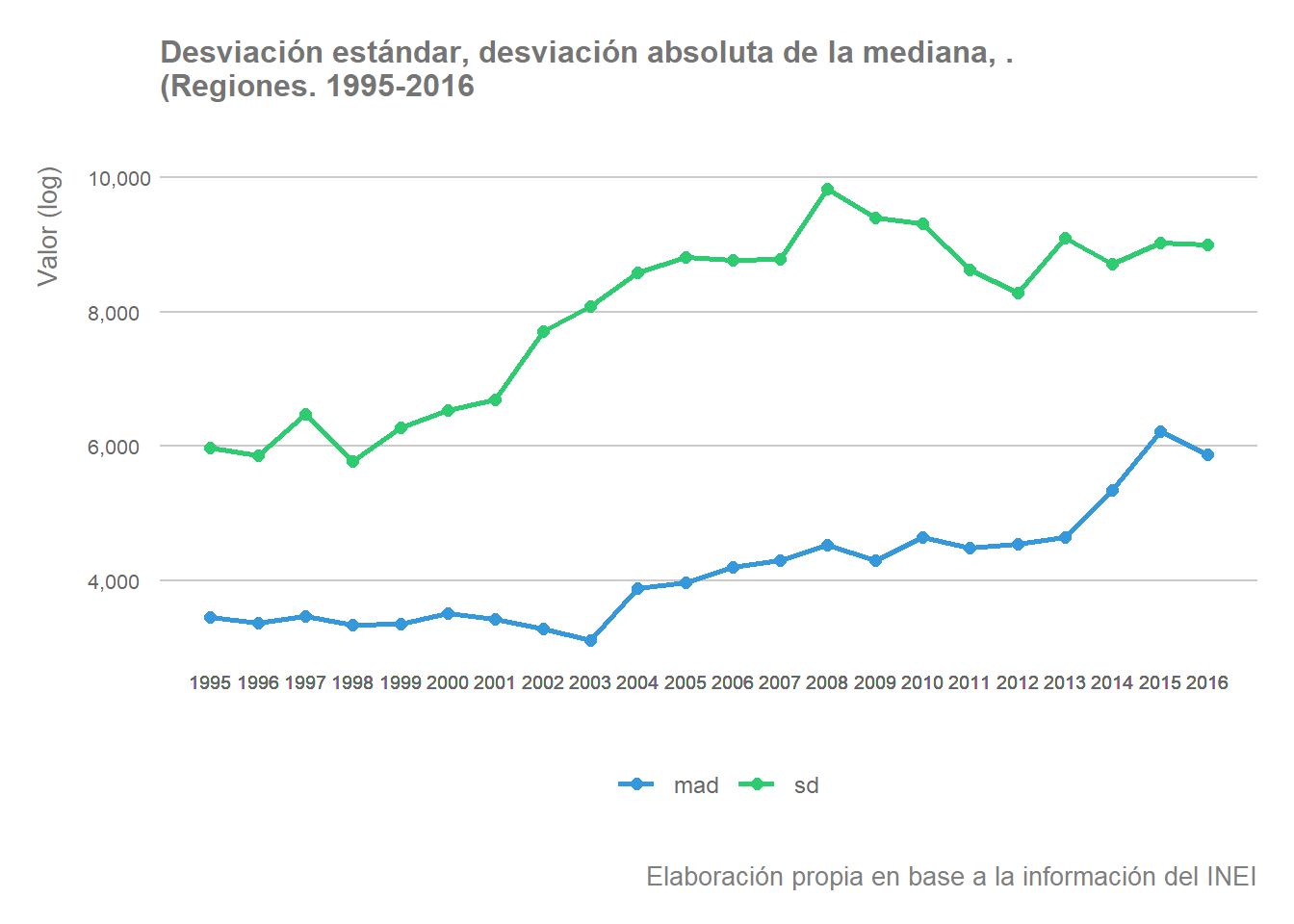
A continuación veamos la evolución de los coeficientes de asimetría y curtosis durante el periodo analizado. El coeficiente de asimetría permite identificar y describir la forma en que los datos tienden a reunirse atendiendo a la frecuencia con que se encuentran dentro de la distribución. La distribución puede ser simétrica o mostrar asimetría positiva (hacia la izquierda) o negativa (hacia la derecha). Por su parte, el coeficiente de curtosis mide el apuntamiento de la distribución. Es decir, evalúa el grado de agudeza o achatamiento de una distribución con respecto a la distribución normal, indicando si las observaciones se encuentran más o menos agrupadas entre sí. Si el coeficiente de curtosis es igual a cero se entiende que la distribución es de carácter mesocúrtico, es decir, el apuntamiento sería normal. Si el coeficiente fuese mayor que cero la distribución sería de carácter leptocúrtico, reflejando que los valores están cercanos a la media (apuntamiento). Por el contrario, si el coeficiente es menor que cero la distribución recibe el nombre de platicúrtica, indicando que los valores se encuentran más alejados de la media, siendo por tanto la distribución más plana de lo normal.
vars_three <- statsperu2 %>%
mutate(year= c(1995:2016)) %>%
dplyr::select(year, skew, kurtosis) %>%
gather(key = variable, value = valor, 2:3) %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
ggplot(vars_three, aes(x= year, y= valor, color = variable)) +
geom_line(size = 1) +
geom_point(size = 2) +
scale_x_date(breaks = vars_one$year, date_labels = "%Y") +
labs(title= "Asimetría y curtosis. \n(Regiones. 1995-2016)",
subtitle="",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="",
color = NULL) +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))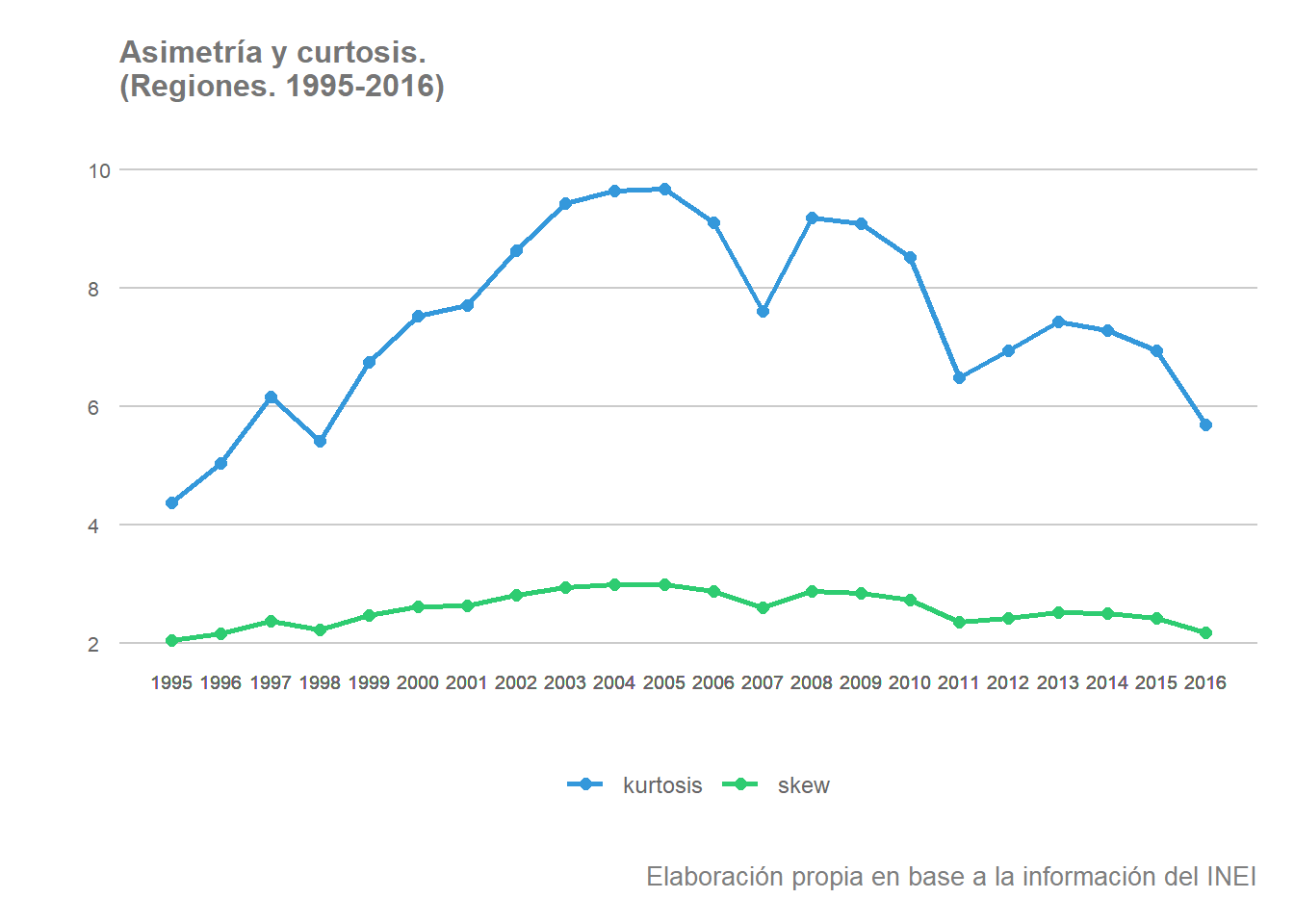
Vemos que la asimetría se mantiene constante a lo largo del periodo, indicando que el número de regiones que se sitúan por encima (o por debajo) del promedio se mantiene prácticamente sin cambios a lo largo del periodo. Esto podría indicar una falta de movilidad y un estancamiento entre el grupo de regiones ricas y el de regiones menos favorecidas. Por su parte, el coeficiente de curtosis es superior a cero, evidenciando que la mayoría de valores se sitúan relativamente cercanos a la media, a pesar de la tendencia descendente en la última década.
Dispersión: Convergencia sigma
A principios de la década de los 90, los economistas Robert Barro y Sala-i-Martín popularizaron los conceptos de convergencias sigma y convergencia beta. Ambos conceptos, a pesar de sus limitaciones, continúan siendo a día de hoy las herramientas más utilizadas para analizar la evolución de las disparidades entre economías. El término de convergencia sigma hace referencia a la dispersión de la variable a estudiar a lo largo del tiempo y evalúa el grado de desigualdad existente entre economías de la variable objeto de estudio. Habría convergencia sigma si se observase una reducción en la dispersión de la variable analizada entre los territorios. Por su parte, la convergencia beta plantea que además de analizar si ha habido una reducción de la dispersión, conviene observar si las economías más pobres han registrado un crecimiento superior a las economías ricas. En el caso de que las economías más desfavorecidas crecieran a un ritmo superior podría darse que en el futuro tuviese lugar el esperado proceso de catching up entre territorios.
Para calcular la existencia de convergencia sigma se suele utilizar la desviación típica del logaritmo de la renta por habitante. No obstante, debido a que dicha metodología no podría aplicarse en el caso de que las variables tomasen valores negativos por el uso de logaritmos, una media alternativa de extendido uso es el coeficiente de variación (CV). El coeficiente de variación ha sido calculado previamente, y su representación gráfica sería la siguiente:
library(data.table)
cv <- setDT(statsperu, keep.rownames = TRUE)[]
cv <- cv %>%
filter(rn == "coef.var" ) %>%
gather(key = variable, value = cv, 2:23) %>%
mutate(year = c(1995:2016)) %>%
dplyr::select(year, cv) %>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
ggplot(cv, aes(x= year, y= cv)) +
geom_line(size = 1) +
geom_point(size = 2) +
scale_x_date(breaks = cv$year, date_labels = "%Y") +
labs(title= "Coeficiente de variación . 1995-2016",
subtitle="",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="",
color = NULL) +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))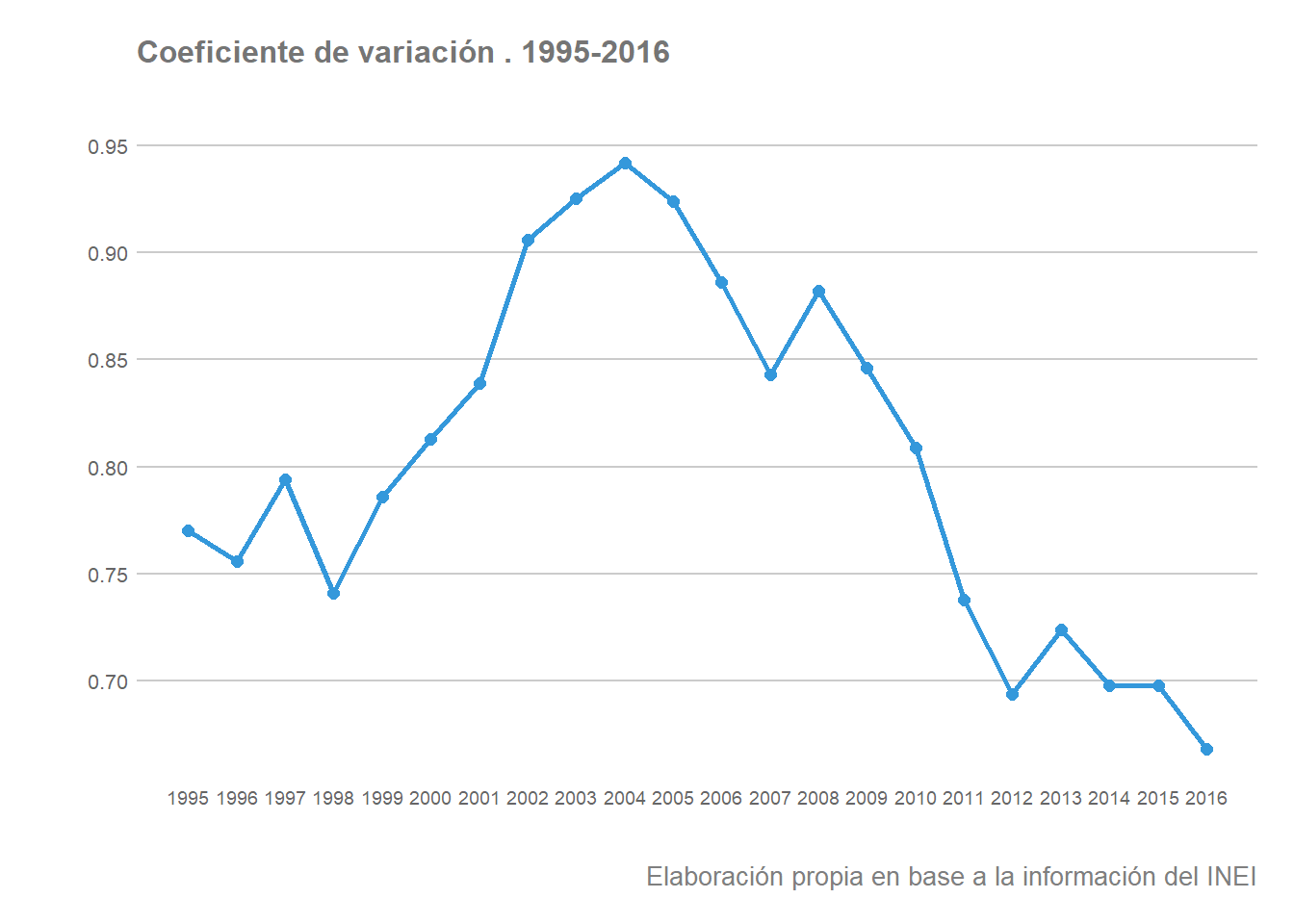
Los datos sugieren que en el periodo 2008-2016 habría tenido lugar convergencias sigma entre las regiones peruanas, aunque la tendencia resulta opuesta para el periodo 1998-2004.
Existen otras formas muy conocidas para determinar la evolución de la desigualdad entre territorios. Entre los más conocidos encontramos el coeficiente de Gini y coeficiente de Theil aunque existen otros como la desigualdad individual o colectiva. La mayoría de indicadores parten de la premisa de que una reducción de la dispersión entre regiones a lo largo del tiempo indicaría la existencia de un proceso de convergencia entre ellas. El cálculo del coeficiente de Gini y de Theil se realiza fácilmente en R con el paquete {ineq}, tal y como se realiza a continuación:
#### indice de Gini
gini_1995 <- ineq(VABpc1995)
gini_1996 <- ineq(VABpc1996)
gini_1997 <- ineq(VABpc1997)
gini_1998 <- ineq(VABpc1998)
gini_1999 <- ineq(VABpc1999)
gini_2000 <- ineq(VABpc2000)
gini_2001 <- ineq(VABpc2001)
gini_2002 <- ineq(VABpc2002)
gini_2003 <- ineq(VABpc2003)
gini_2004 <- ineq(VABpc2004)
gini_2005 <- ineq(VABpc2005)
gini_2006 <- ineq(VABpc2006)
gini_2007 <- ineq(VABpc2007)
gini_2008 <- ineq(VABpc2008)
gini_2009 <- ineq(VABpc2009)
gini_2010 <- ineq(VABpc2010)
gini_2011 <- ineq(VABpc2011)
gini_2012 <- ineq(VABpc2012)
gini_2013 <- ineq(VABpc2013)
gini_2014 <- ineq(VABpc2014)
gini_2015 <- ineq(VABpc2015)
gini_2016 <- ineq(VABpc2016)
peru_gini <- data.frame(gini_1995, gini_1996,gini_1997, gini_1998, gini_1999, gini_2000, gini_2001, gini_2002, gini_2003, gini_2004, gini_2005, gini_2006, gini_2007, gini_2008, gini_2009, gini_2010, gini_2011, gini_2012, gini_2013, gini_2014, gini_2015, gini_2016)
# indice de theil:
theil_1995 <- Theil(VABpc1995)
theil_1996 <- Theil(VABpc1996)
theil_1997 <- Theil(VABpc1997)
theil_1998 <- Theil(VABpc1998)
theil_1999 <- Theil(VABpc1999)
theil_2000 <- Theil(VABpc2000)
theil_2001 <- Theil(VABpc2001)
theil_2002 <- Theil(VABpc2002)
theil_2003 <- Theil(VABpc2003)
theil_2004 <- Theil(VABpc2004)
theil_2005 <- Theil(VABpc2005)
theil_2006 <- Theil(VABpc2006)
theil_2007 <- Theil(VABpc2007)
theil_2008 <- Theil(VABpc2008)
theil_2009 <- Theil(VABpc2009)
theil_2010 <- Theil(VABpc2010)
theil_2011 <- Theil(VABpc2011)
theil_2012 <- Theil(VABpc2012)
theil_2013 <- Theil(VABpc2013)
theil_2014 <- Theil(VABpc2014)
theil_2015 <- Theil(VABpc2015)
theil_2016 <- Theil(VABpc2016)
peru_theil <- data.frame(theil_1995, theil_1996, theil_1997, theil_1998, theil_1999, theil_2000, theil_2001, theil_2002, theil_2003, theil_2004, theil_2005, theil_2006, theil_2007, theil_2008, theil_2009, theil_2010, theil_2011, theil_2012, theil_2013, theil_2014, theil_2015, theil_2016)
p_gini <- peru_gini %>%
gather(key = gini_year, value = gini) %>%
mutate(year = c(1995:2016)) %>%
dplyr::select(year, gini)%>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
p_theil <- peru_theil %>%
gather(key = theil_year, value = theil) %>%
mutate(year = c(1995:2016)) %>%
dplyr::select(year, theil)%>%
mutate(year = as.Date(paste(year, "-01-01", sep = "", format='%Y-%b-%d')))
gini_theil <- left_join(p_gini, p_theil)
## Joining, by = "year"
gini_theil <- gini_theil %>%
gather(key = variable, value = valor, 2:3)
Gráficamente la evolución de dichos indicadores será la siguiente:
ggplot(gini_theil, aes(x= year, y= valor, color = variable)) +
geom_line(size = 1) +
geom_point(size = 2) +
scale_x_date(breaks = gini_theil$year, date_labels = "%Y") +
labs(title= "Coeficiente de Gini y Coeficiente de Theil. 1995-2016",
subtitle="",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="",
color = NULL) +
theme_lab() +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))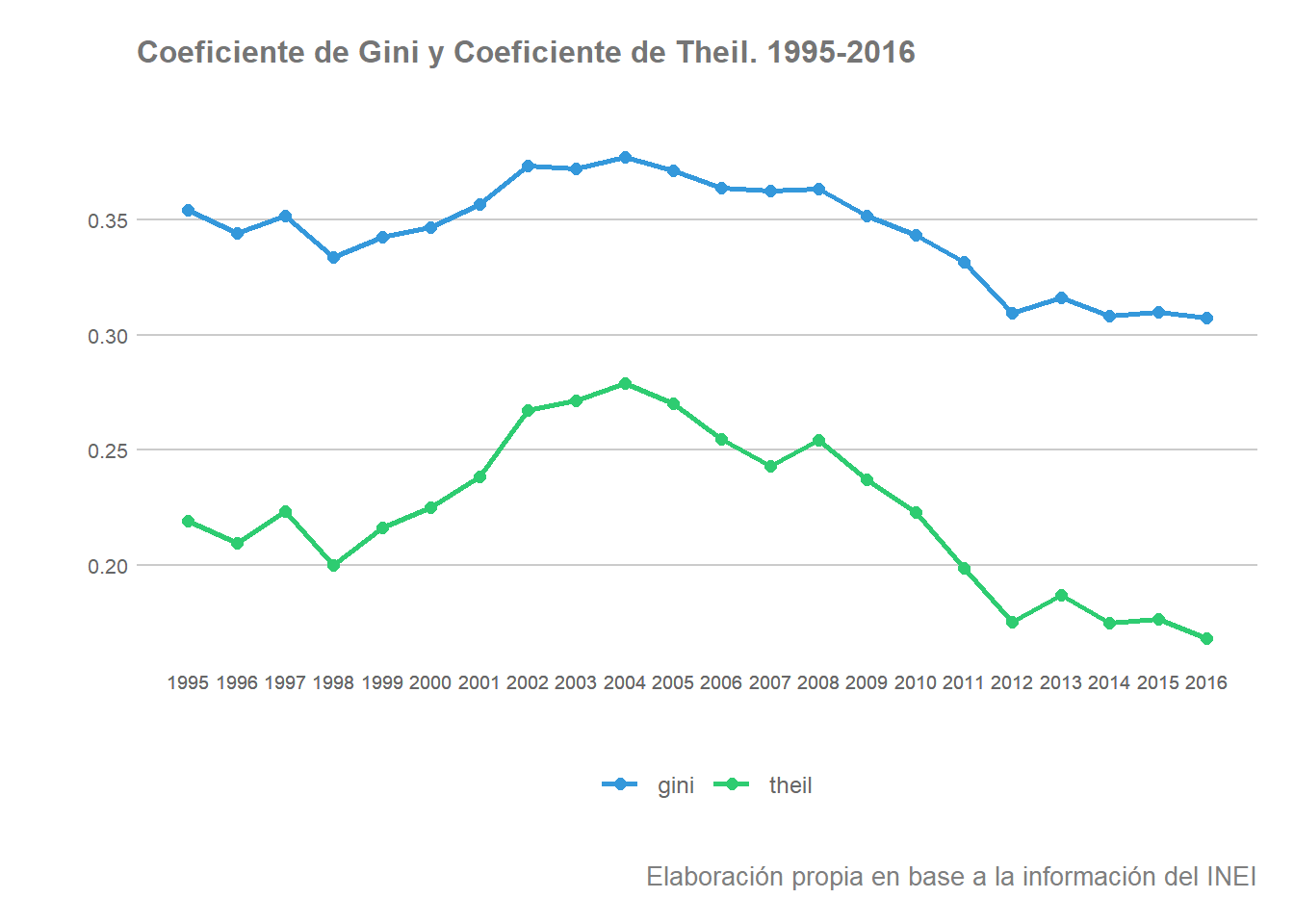
Podemos comparar la evolución de los tres coeficientes utilizando números índices de la siguiente forma:
g_t <- left_join(p_gini, p_theil)
## Joining, by = "year"
g_t_v <- left_join(g_t, cv)
## Joining, by = "year"
gtv_index <- transform(g_t_v,
gini.index = 100*gini/gini[6],
theil.index = 100*theil/theil[6],
cv.index = 100*cv/cv[6])
gtv_index <- gtv_index %>%
dplyr::select(year, gini.index, theil.index, cv.index) %>%
gather(key = variable, value = valor, 2:4)
ggplot(gtv_index, aes(x= year, y= valor, color = variable)) +
geom_line(size = 1) +
geom_point(size = 2) +
scale_x_date(breaks = gini_theil$year, date_labels = "%Y") +
labs(title= "Coeficiente de Gini, coeficiente de Theil y coeficiente de variación. 1995-2016",
subtitle="(2000 = 100)",
caption= "Elaboración propia en base a la información del INEI",
x= NULL,
y="",
color = NULL) +
theme_lab() +
geom_vline(xintercept = as.Date("2000-01-01"), color = "red", size = 1, linetype="dotted") +
theme(
legend.position = "bottom",
axis.text.y = element_text(hjust = 0,
colour = "grey40",
size = 8),
axis.text.x=element_text(colour="grey40",
size = 7),
plot.title=element_text(size = 12,
hjust = 0),
plot.subtitle = element_text(size = 9,
hjust = 0),
text = element_text(size = 10),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank(),
#legend.title = element_text(color = "grey40", size = 7),
legend.text = element_text(color = "grey40", size = 9, hjust = 0))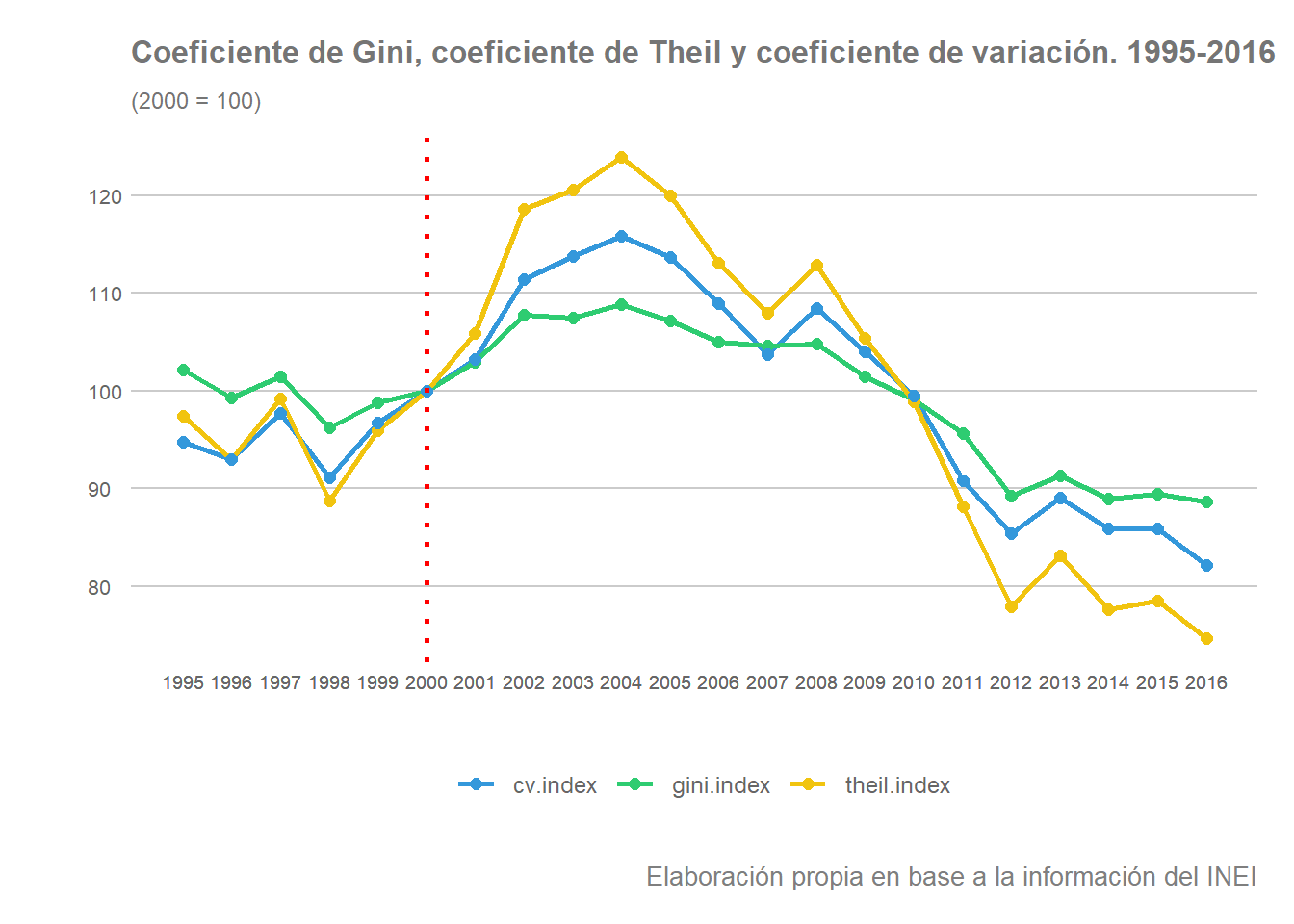
Todo parece indicar que desde el año 2008 ha tenido lugar una tendencia descendente en la dispersión de la renta por habitante entre regiones. Es decir, habría tenido lugar un proceso de convergencia sigma durante dicho periodo. Debemos sin embargo tener en cuenta que los coeficientes calculados nos ofrecen el resultado agregado para el conjunto de observaciones y, por tanto, no vemos el posible comportamiento especial de algunas regiones individualizadas o el posible comportamiento singular de subgrupos de regiones. De hecho, como vimos anteriormente, todo parece indicar que el comportamiento del promedio regional está fuertemente influenciado por un grupo reducido de regiones, especialmente por el de Moquegua, regiones de mayor nivel de VAB por habitante. El comportamiento de estas regiones con seguridad habrá influenciado la evolución de los coeficientes de dispersión examinados, dinámicas que la convergencia sigma, por si sola y para el conjunto de observaciones no nos permite identificar.
Convergencia Beta.
Como expusimos, el objetivo del análisis de convergencia beta consiste en comprobar si entre un conjunto de economías, aquellas en una situación de atraso relativo han ido reduciendo la brecha existente con respecto a las economías avanzadas en un periodo de tiempo determinado. Se entiende que para que ello suceda las economías atrasadas deben mostrar tasas de crecimiento superiores. En el caso de que dicha dinámica tuviera lugar se podría decir que está teniendo un proceso de catching up de las primeras sobre las segundas. Por tanto, se dice que una condición necesaria, aunque no suficiente, para la existencia de convergencia sigma es la existencia de convergencia beta y, además, se considera que la existencia de convergencia beta tenderá a generar convergencia sigma.
La existencia de convergencia beta absoluta se determina a través de un análisis de regresión con una variable dependiente y una variable independiente, donde la primera es la tasa de crecimiento del VAB por habitante y la segunda es el nivel inicial de dicha variable. Un resultado negativo sería indicativo de convergencia mientras que uno positivo sería señal de divergencia entre las economías analizadas. Por consiguiente, siguiendo la explicación, la convergencia beta para el periodo 1995-2016 sería:
lm((1/21)*log(`2016`/`1995`)~log(`1995`),data=BD_VABpc)
##
## Call:
## lm(formula = (1/21) * log(`2016`/`1995`) ~ log(`1995`), data = BD_VABpc)
##
## Coefficients:
## (Intercept) log(`1995`)
## 0.12604 -0.01114
summary(lm((1/21)*log(`2016`/`1995`)~log(`1995`),data = BD_VABpc))
##
## Call:
## lm(formula = (1/21) * log(`2016`/`1995`) ~ log(`1995`), data = BD_VABpc)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.023942 -0.008650 -0.001103 0.005798 0.031283
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.126040 0.038934 3.237 0.00378 **
## log(`1995`) -0.011144 0.004435 -2.513 0.01981 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01291 on 22 degrees of freedom
## Multiple R-squared: 0.223, Adjusted R-squared: 0.1877
## F-statistic: 6.313 on 1 and 22 DF, p-value: 0.01981
Para el conjunto del periodo habría convergencia beta (Significativa al 0.05) donde el valor de beta sería -0.01114. Gráficamente la regresión anterior se podría representar de la siguiente forma. En términos generales los datos indican que, por lo general, las regiones que partían de un menor nivel de renta por habitante en el año inicial habrían registrado un crecimiento superior que las regiones que partían de un mayor nivel de renta per cápita en 1995. Apurímac se sitúa como la región de mayor crecimiento aunque, no obstante, en los boxplot realizados al inicio del post, esta región registraría un outlier en un año, exactamente en el año 2016.
ggplot(BD_VABpc, aes(x = log(`1995`), y = (1/21)*log(`2016`/`1995`))) +
geom_point(color = "orange") +
geom_smooth(method="lm", se=FALSE, colour="grey40", size=0.5) +
geom_text_repel(aes(label=Name), size=2, colour="Black") +
theme_classic() +
labs(title = "convergencia beta 1995-2016",
subtitle = "",
y = "crecimiento 1995-2016",
x = "VABpc en 1995 (log)")
## `geom_smooth()` using formula 'y ~ x'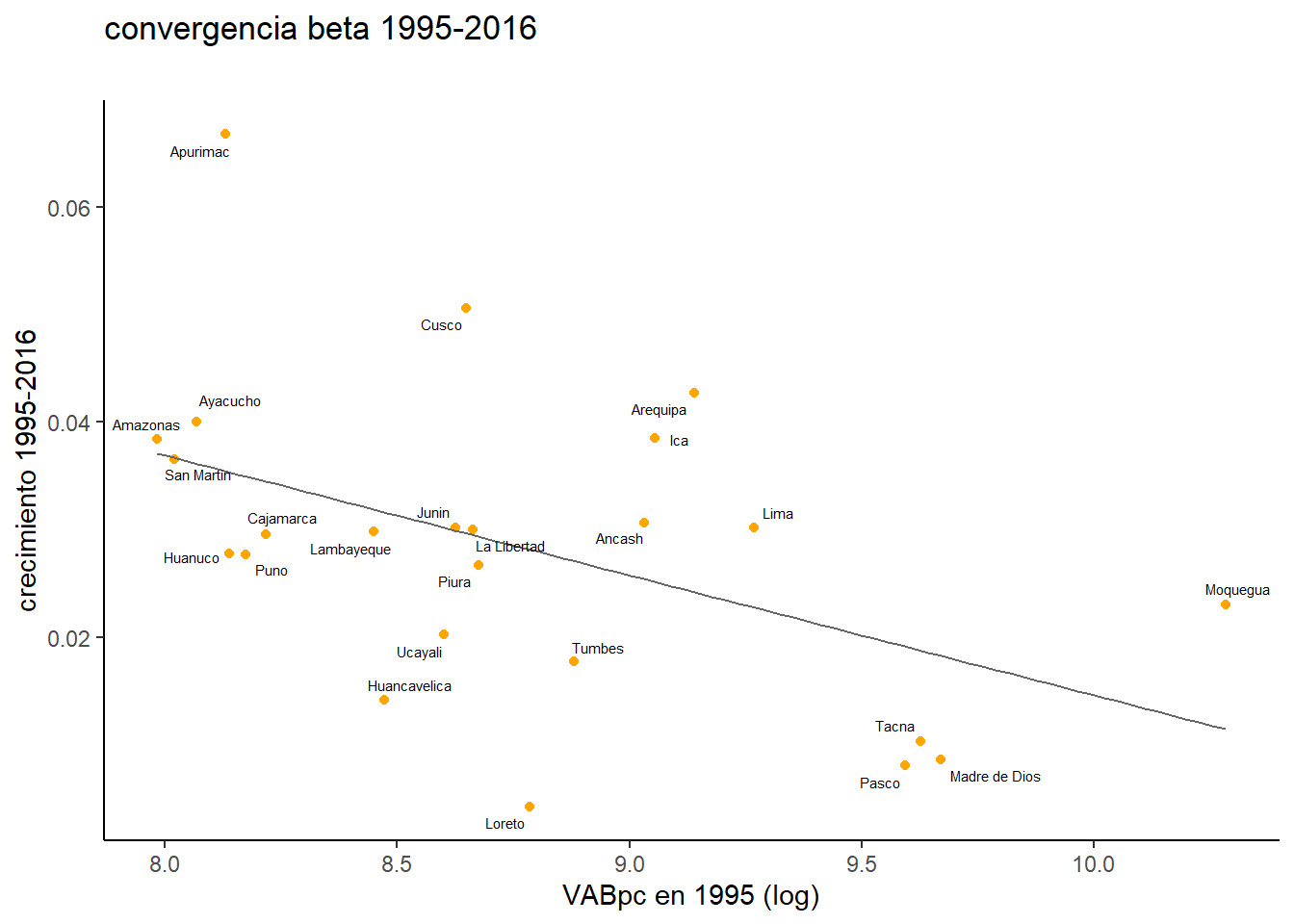
Si realizamos la misma operativa para distintos subgrupos de periodos se comprueba que donde más significativa habría sido la convergencia beta es en el periodo 2008-2016. Por tanto, los resultados de la convergencia beta se complementan con los obtenidos previamente, aunque la dinámica convergente parece ser en mayor medida resultado de un menor crecimiento relativo de las regiones que partían de una situación inicial más favorable.
# 1995-2016
y_1995_2016 <- lm((1/21)*log(`2016`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2016 <- coef(summary(y_1995_2016))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2000
y_1995_2000 <- lm((1/5)*log(`2000`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2000 <- coef(summary(y_1995_2000))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 2000-2004
y_2000_2004 <- lm((1/4)*log(`2004`/`2000`)~log(`2000`),data=BD_VABpc)
c_2000_2004 <- coef(summary(y_2000_2004))["log(`2000`)", c("Estimate", "Pr(>|t|)")]
# 2004-2008
y_2004_2008 <- lm((1/4)*log(`2008`/`2004`)~log(`2004`),data=BD_VABpc)
c_2004_2008 <- coef(summary(y_2004_2008))["log(`2004`)", c("Estimate", "Pr(>|t|)")]
# 2008-2016
y_2008_2016 <- lm((1/8)*log(`2016`/`2008`)~log(`2008`),data=BD_VABpc)
c_2008_2016 <- coef(summary(y_2008_2016))["log(`2008`)", c("Estimate", "Pr(>|t|)")]
# 1995-2001
y_1995_2001 <- lm((1/6)*log(`2001`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2001 <- coef(summary(y_1995_2001))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2002
y_1995_2002 <- lm((1/7)*log(`2002`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2002 <- coef(summary(y_1995_2002))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2003
y_1995_2003 <- lm((1/8)*log(`2003`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2003 <- coef(summary(y_1995_2003))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2004
y_1995_2004 <- lm((1/9)*log(`2004`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2004 <- coef(summary(y_1995_2004))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2005
y_1995_2005 <- lm((1/10)*log(`2005`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2005 <- coef(summary(y_1995_2005))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2006
y_1995_2006 <- lm((1/11)*log(`2006`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2006 <- coef(summary(y_1995_2006))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2007
y_1995_2007 <- lm((1/12)*log(`2007`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2007 <- coef(summary(y_1995_2007))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2008
y_1995_2008 <- lm((1/13)*log(`2008`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2008 <- coef(summary(y_1995_2008))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2009
y_1995_2009 <- lm((1/14)*log(`2009`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2009 <- coef(summary(y_1995_2009))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2010
y_1995_2010 <- lm((1/15)*log(`2010`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2010 <- coef(summary(y_1995_2010))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2011
y_1995_2011 <- lm((1/16)*log(`2011`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2011 <- coef(summary(y_1995_2011))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2012
y_1995_2012 <- lm((1/17)*log(`2012`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2012 <- coef(summary(y_1995_2012))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2013
y_1995_2013 <- lm((1/18)*log(`2013`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2013 <- coef(summary(y_1995_2013))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2014
y_1995_2014 <- lm((1/19)*log(`2014`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2014 <- coef(summary(y_1995_2014))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2015
y_1995_2015 <- lm((1/20)*log(`2015`/`1995`)~log(`1995`),data=BD_VABpc)
c_1995_2015 <- coef(summary(y_1995_2015))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
df <- data.frame(c_1995_2016,
c_1995_2000,
c_2000_2004,
c_2004_2008,
c_2008_2016,
c_1995_2001,
c_1995_2002,
c_1995_2003,
c_1995_2004,
c_1995_2005,
c_1995_2006,
c_1995_2007,
c_1995_2008,
c_1995_2009,
c_1995_2010,
c_1995_2011,
c_1995_2012,
c_1995_2013,
c_1995_2014,
c_1995_2015)
df <- setDT(df, keep.rownames = TRUE)[]
df <- df %>%
gather(key = periodo, value = valor, 2:21) %>%
spread(rn, valor)
datatable(df)
Sin embargo, un aspecto de especial relevancia en un país tan heterogéneo como Perú es la gran disparidad existente entre las regiones en aspectos muy diversos. Para el caso que nos ocupa, resulta de especial relevancia el hecho de que las regiones peruanas son notablemente heterogéneas en tamaño, no solo en términos de superficie sino también en población, en población ocupada, etc. En nuestro caso la región de Lima incluye Lima metropolitana y, por tanto, el tamaño de esta región equivale a aproximadamente una tercera parte de la población total del país. Por el contrario, regiones como Moquegua, representan solo una pequeña parte del conjunto de la población del país. Es por ello que será relevante examinar la existencia de convergencia beta teniendo en cuenta estas disparidades poblacionales, en tanto en cuanto el análisis de convergencia beta tradicional otorgaría el mismo peso a regiones de gran tamaño como Lima que a regiones pequeñas como Moquegua o Madre de Dios.
pob_94_17 <- read_excel("C:/Users/Usuario/Desktop/r_que_r/r_que_r/content/datasets/1994_2016_POBLACION_DEP.xlsx")
peru_df <- inner_join(BD_VABpc, pob_94_17)
## Joining, by = c("Name", "id")
ggplot(peru_df, aes(x = log(`1995`), y = (1/21)*log(`2016`/`1995`))) +
geom_point(aes(size = pob_2016, fill = `2016`),
shape = 21,
colour = "#999999",
alpha = 0.5) +
geom_smooth(method="lm", se=FALSE, colour="red", size = 1)+
geom_smooth(method="lm", se=FALSE, colour="red", aes(weight=pob_2016),
linetype = 2, size = 1)+
scale_size_continuous(range = c(1, 30)) +
geom_text_repel(aes(label=Name), size=2, colour="Black") +
theme_classic() +
scale_fill_viridis() +
labs(title = "convergencia beta 1995-2016",
subtitle = "(ponderado por población en 2016)",
y = "crecimiento 1995-2016",
x = "VABpc en 1995 (log)")
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'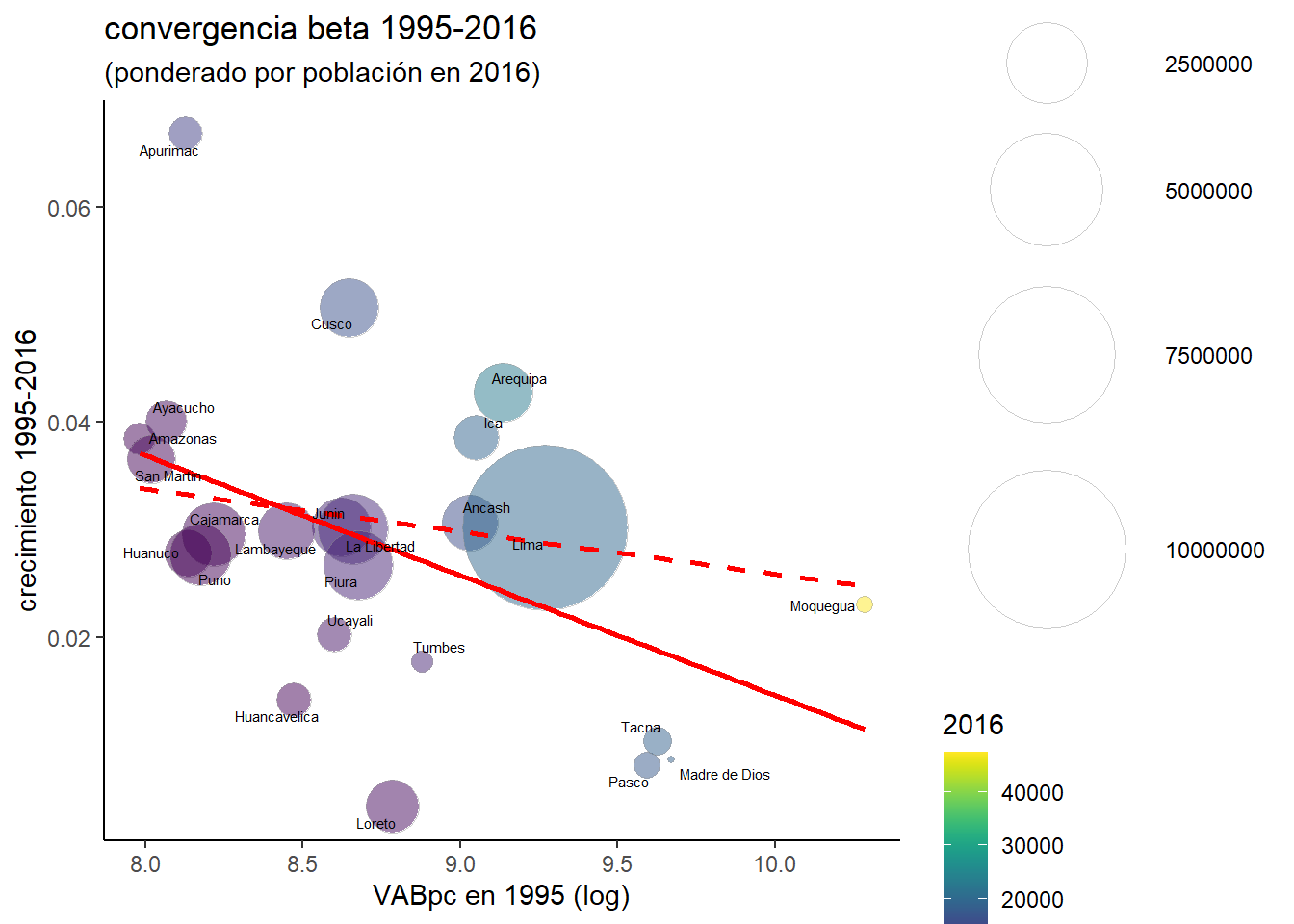
Comprobamos que ponderando por población la convergencia beta para el conjunto del periodo habría sido de mucha menor magnitud (línea discontinua). Veamos gráficamente como habría sido la convergencia beta del periodo 2008-2016 ponderando también por población
ggplot(peru_df, aes(x = log(`2008`), y = (1/8)*log(`2016`/`2008`))) +
geom_point(aes(size = pob_2016, fill = `2016`),
shape = 21,
colour = "#999999",
alpha = 0.5) +
geom_smooth(method="lm", se=FALSE, colour="red", size = 1)+
geom_smooth(method="lm", se=FALSE, colour="red", aes(weight=pob_2016),
linetype = 2, size = 1)+
scale_size_continuous(range = c(1, 30)) +
geom_text_repel(aes(label=Name), size=2, colour="Black") +
theme_classic() +
scale_fill_viridis() +
labs(title = "convergencia beta 2008-2016",
subtitle = "(ponderado por población en 2016)",
y = "crecimiento 2008-2016",
x = "VABpc en 2008 (log)")
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'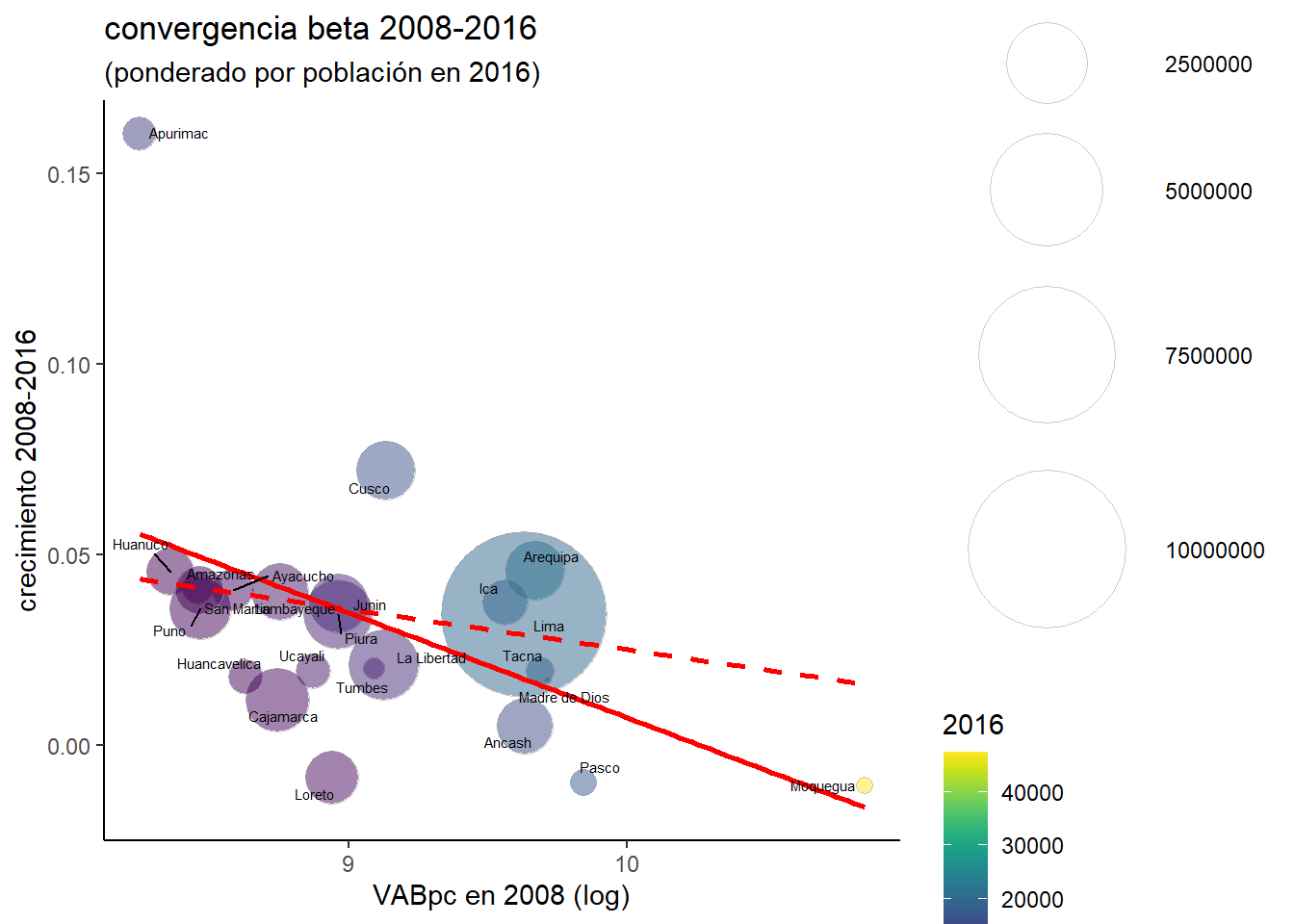
De nuevo, el valor de dicho proceso de convergencia, incluso en el periodo que se comprobaba de mayor dinámica convergente, registra un valor mucho más reducido. De hecho, si observamos los coeficientes de la regresión para distintos periodos, al igual que hicimos previamente, comprobamos que a excepción del periodo 1995-2000 no habría tenido lugar convergencia beta que fuese estadísticamente significativa. Resulta evidente que el comportamiento de Lima en relación al del resto de regiones influirá notablemente en el resultado de la regresión cuando se tiene en cuenta el tamaño departamental.
# 1995-2016
y_1995_2016 <- lm((1/21)*log(`2016`/`1995`)~log(`1995`), data=peru_df, weights= pob_2016)
c_1995_2016 <- coef(summary(y_1995_2016))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2000
y_1995_2000 <- lm((1/5)*log(`2000`/`1995`)~log(`1995`), data=peru_df, weights= pob_2000)
c_1995_2000 <- coef(summary(y_1995_2000))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 2000-2004
y_2000_2004 <- lm((1/4)*log(`2004`/`2000`)~log(`2000`), data=peru_df, weights= pob_2004)
c_2000_2004 <- coef(summary(y_2000_2004))["log(`2000`)", c("Estimate", "Pr(>|t|)")]
# 2004-2008
y_2004_2008 <- lm((1/4)*log(`2008`/`2004`)~log(`2004`), data=peru_df, weights= pob_2008)
c_2004_2008 <- coef(summary(y_2004_2008))["log(`2004`)", c("Estimate", "Pr(>|t|)")]
# 2008-2016
y_2008_2016 <- lm((1/8)*log(`2016`/`2008`)~log(`2008`), data=peru_df, weights= pob_2016)
c_2008_2016 <- coef(summary(y_2008_2016))["log(`2008`)", c("Estimate", "Pr(>|t|)")]
# 1995-2001
y_1995_2001 <- lm((1/6)*log(`2001`/`1995`)~log(`1995`), data=peru_df, weights= pob_2001)
c_1995_2001 <- coef(summary(y_1995_2001))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2002
y_1995_2002 <- lm((1/7)*log(`2002`/`1995`)~log(`1995`), data=peru_df, weights= pob_2002)
c_1995_2002 <- coef(summary(y_1995_2002))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2003
y_1995_2003 <- lm((1/8)*log(`2003`/`1995`)~log(`1995`), data=peru_df, weights= pob_2003)
c_1995_2003 <- coef(summary(y_1995_2003))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2004
y_1995_2004 <- lm((1/9)*log(`2004`/`1995`)~log(`1995`), data=peru_df, weights= pob_2004)
c_1995_2004 <- coef(summary(y_1995_2004))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2005
y_1995_2005 <- lm((1/10)*log(`2005`/`1995`)~log(`1995`), data=peru_df, weights= pob_2005)
c_1995_2005 <- coef(summary(y_1995_2005))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2006
y_1995_2006 <- lm((1/11)*log(`2006`/`1995`)~log(`1995`), data=peru_df, weights= pob_2006)
c_1995_2006 <- coef(summary(y_1995_2006))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2007
y_1995_2007 <- lm((1/12)*log(`2007`/`1995`)~log(`1995`), data=peru_df, weights= pob_2007)
c_1995_2007 <- coef(summary(y_1995_2007))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2008
y_1995_2008 <- lm((1/13)*log(`2008`/`1995`)~log(`1995`), data=peru_df, weights= pob_2008)
c_1995_2008 <- coef(summary(y_1995_2008))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2009
y_1995_2009 <- lm((1/14)*log(`2009`/`1995`)~log(`1995`), data=peru_df, weights= pob_2009)
c_1995_2009 <- coef(summary(y_1995_2009))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2010
y_1995_2010 <- lm((1/15)*log(`2010`/`1995`)~log(`1995`), data=peru_df, weights= pob_2010)
c_1995_2010 <- coef(summary(y_1995_2010))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2011
y_1995_2011 <- lm((1/16)*log(`2011`/`1995`)~log(`1995`), data=peru_df, weights= pob_2011)
c_1995_2011 <- coef(summary(y_1995_2011))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2012
y_1995_2012 <- lm((1/17)*log(`2012`/`1995`)~log(`1995`), data=peru_df, weights= pob_2012)
c_1995_2012 <- coef(summary(y_1995_2012))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2013
y_1995_2013 <- lm((1/18)*log(`2013`/`1995`)~log(`1995`), data=peru_df, weights= pob_2013)
c_1995_2013 <- coef(summary(y_1995_2013))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2014
y_1995_2014 <- lm((1/19)*log(`2014`/`1995`)~log(`1995`), data=peru_df, weights= pob_2014)
c_1995_2014 <- coef(summary(y_1995_2014))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
# 1995-2015
y_1995_2015 <- lm((1/20)*log(`2015`/`1995`)~log(`1995`), data=peru_df, weights= pob_2015)
c_1995_2015 <- coef(summary(y_1995_2015))["log(`1995`)", c("Estimate", "Pr(>|t|)")]
df_2 <- data.frame(c_1995_2016,
c_1995_2000,
c_2000_2004,
c_2004_2008,
c_2008_2016,
c_1995_2001,
c_1995_2002,
c_1995_2003,
c_1995_2004,
c_1995_2005,
c_1995_2006,
c_1995_2007,
c_1995_2008,
c_1995_2009,
c_1995_2010,
c_1995_2011,
c_1995_2012,
c_1995_2013,
c_1995_2014,
c_1995_2015)
library(data.table)
df_2 <- setDT(df_2, keep.rownames = TRUE)[]
df_2 <- df_2 %>%
gather(key = periodo, value = valor, 2:21) %>%
spread(rn, valor)
datatable(df_2)